スピーカーの音場補正プログラムを自作してみた

2024年4月16日 17:31

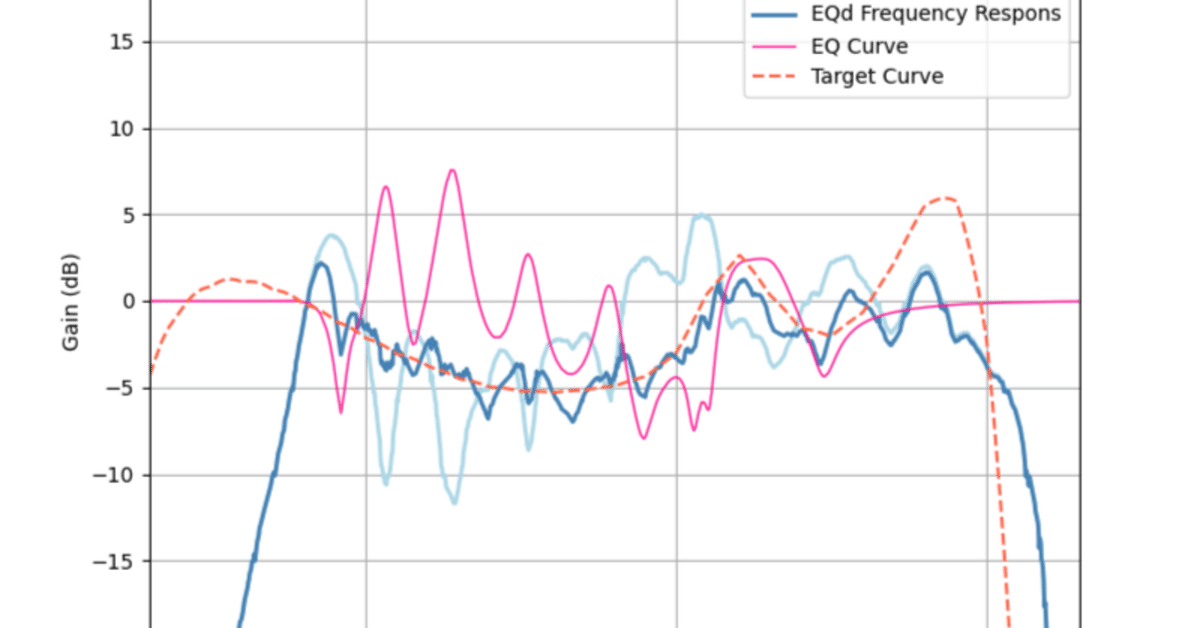
まずは以下のグラフをご覧下さい。

デコボコしているグラフですね。

これは我が家のスピーカー（Yamaha MSP3）の周波数特性をマイクで計測したものです。ご覧の通り、フラットとは言い難い特性です。このデコボコはスピーカーそのものがもつ周波数特性と、部屋の壁からの反響などで特定の周波数が強調されたり打ち消されたりした結果の足し合わせとして生じています。
一般に、フラットな周波数特性であるほど、原音再現性が高いと考えられています。すなわち、音楽をより「本来の形」で聴くことができる、ということです。
そのため、このデコボコしている周波数特性をイコライザーなどで補正してフラットにしてやる、という「音場補正」という考えが存在します。

最近DTM界隈ではIK Multimediaの「ARC STUDIO」という音場補正機器が話題です。スピーカーの音質がとても良くなるらしいです。
しかし、ハードの音場補正装置としては破格の安さだとはいえ、5万くらいするものなのでほいほいと買えるものではありません。なので、フリーで使える音場補正プログラムを探してみました。

フリーの音場補正プログラム

有名なものでは「Room EQ Wizard（REW）」というソフトがあり、測定から補正用イコライザー設定の作成まで行うことができます。冒頭のグラフも、REWで測定した結果をグラフで描画したものです。REWで作成したイコライザー設定を、たとえばWindowsだと「Equalizer APO」というこれまたフリーのソフトでPCから流れる音にイコライザーを適用することで、完全フリーの音場補正が可能となります。

では、そうして補正した結果の音はどのようなものになるのでしょうか？

正直なところ、お世辞にも「音質が良くなった」といえるようなものではないと思いました。なにか音が曇った感じ、引っ込んだ感じがして、言ってみれば「つまらない音」になってしまった感じがするのです（ただ音の定位は改善された気はしました）。
なので原音と補正後の音を適当なDry/Wet比でミックスしてやる、というようなこともしてみましたが、そもそもこの音場補正は本当に正しいのか、という疑問が湧いてきました。

音場補正を式で現してみる

そもそも、音場補正は「何を目標にして」補正するのでしょうか。
それはスタジオの再生環境です。スタジオの再生環境を自宅のスピーカーで再現できれば、音楽をより「本来の」音で聴くことができる、という考えです。では、スタジオの再生環境とはどのようなものでしょうか。一般に、それはフラットな周波数特性であると考えられます（あるいは適切なスロープやカーブをもった周波数特性です）。
では、なぜフラットな周波数特性なのでしょうか。
理想的には、耳で聴く音楽は「人間の耳で聴いて」全周波数域でフラットに聞こえることが望ましいと言われます。すなわち、より正確に言えば、「音源そのものがもつ周波数特性」と「スタジオの再生環境の周波数特性」を足し合わせたとき、それが「人間の耳で聴いて」フラットな特性になればよい、ということです。

わかりやすく式にしてみましょう。
上記より、以下の式が成り立つはずです。

$${(音源の周波数特性)+(スタジオの再生環境の周波数特性)=(「人間の耳で聴いて」フラットな特性)}$$

式(1)

では、これを自宅のスピーカー環境で再現することを考えましょう。すなわち、

$${(スタジオの再生環境の周波数特性)=(自宅のスピーカーの周波数特性)+(自宅の部屋の周波数特性)+(音場補正)}$$

式(2)

これを最初の式に代入すると、

$${(音源の周波数特性)+(自宅のスピーカーの周波数特性)+(自宅の部屋の周波数特性)+(音場補正)=(「人間の耳で聴いて」フラットな特性)}$$

式(3)

ここで、一般的な音源は「人間の耳で聴いてフラットな特性」を目指して作られている、という仮定をします。しかし完璧ではないので、ここに適当な傾きをつけて補正してやるとすると、

$${(人間の耳で聴いてフラットな特性)=(音源の周波数特性)+(適当な傾き)}$$

式(4)

すなわち、

$${(音場補正)=-(スピーカーの周波数特性)-(部屋の周波数特性)+(適当な傾き)}$$

式(5)

ここで、(適当な傾き)とはいわゆるターゲットカーブのことを指すと考えられます。

$${(適当な傾き)=(ターゲットカーブ)}$$

式(6)

よって、

$${(音場補正)=-(スピーカーの周波数特性)-(部屋の周波数特性)+(ターゲットカーブ)}$$

式(7)

スピーカーの周波数特性を相殺して、ターゲットカーブに近づける。これが一般的な音場補正の考え方です。

しかし、このようにして求められた音場補正では、先に述べた通り、音が曇ったり引っ込んだりと、あまり良い結果にはなりませんでした。

なにが悪いのでしょうか？

ここまでの式で怪しい部分を探ってみると、式(4)が目につきます。「適当な傾き」とありますが、これはどうやって決まるのでしょうか？　明らかに適当です。
なので、ここをもう少し厳密に考えてみましょう。

等ラウドネス曲線

等ラウドネス曲線、というものがあります。
以下、Wikipediaからの引用です。

等ラウドネス曲線（とうラウドネスきょくせん、英語: Equal loudness contour）は等しい音の大きさと感じる周波数と音圧のマップを等高線として結んだものである。

出典：Wikipedia「等ラウドネス曲線」

グラフにすると以下の様なものです。

これは人間の聴覚特性を数字で表現したものです。この線に沿ったラインを、人間は「フラットな音」であると聴覚上感じます。

よって、「人間の耳で聴いてフラットな特性」とは、厳密に言えばこの等ラウドネス曲線を相殺するような特性である、ということが言えると思います。

$${(人間の耳で聴いてフラットな特性)=-(等ラウドネス曲線)}$$

式(8)

これを式(3)に代入して解くと、

$${(音場補正)=-((等ラウドネス曲線)+(音源の周波数特性)+(スピーカーの周波数特性)+(部屋の周波数特性))}$$

式(9)

これこそが、「より厳密な」音場補正を求める式、なのではないかと考えられます。

しかし実際には、スタジオの再生環境は人為的になんらかのターゲットカーブを目指して調整されている部分もあると思います。なので式(7)の要素もやはり無視する事はできず、ある程度は考える必要があるでしょう。

よって、最終的に求める音場補正は以下の式となります。

$${(音場補正)=α×((ターゲットカーブ)-(スピーカーの周波数特性)-(部屋の周波数特性))+(1-α)×(-(等ラウドネス曲線)-(音源の周波数特性)-(スピーカーの周波数特性)-(部屋の周波数特性))}$$

式(10)

ここで、αは二つの音場補正のミックス率です。

追記（2024/4/17）：聴覚上、人間の耳で聴いてフラットな特性にするには、どこかで等ラウドネス曲線を相殺しなければなりません。その相殺を100%スピーカー側が行うとしたのが音源をフラットと仮定した場合の式(10)の右辺第一項、逆に100%音源側が行うとしたのがターゲットカーブをフラットと仮定した場合の右辺第二項です。実際はこの両極の中間に解があると考えられるため、そこをαの値で調整する、という考えです。

追記（2024/4/21）：ヘッドフォンの場合は頭部伝達関数（HRTF）から外耳道の伝達特性を差し引いたものが目標カーブになると考えられるため、式(8)が以下のようになります。

$${(人間の耳で聴いてフラットな特性)=-(等ラウドネス曲線)+(HRTF-外耳道の伝達特性)}$$

式(8b)

よって、式(10)は以下の様になります。

$${(音場補正)=α×((ターゲットカーブ)-(ヘッドフォンの周波数特性))+(1-α)×((HRTF-外耳道の伝達特性)-(等ラウドネス曲線)-(音源の周波数特性)-(ヘッドフォンの周波数特性))}$$

式(10b)

音場補正プログラムの作成

ということで、目指すべき音場補正の形が厳密に求まったので、それを計算するプログラムを作ってみました。以下、GitHubの公開先です。

このプログラムでは、式(10)に従って音場補正用のイコライジング設定を、スピーカーの周波数特性データをインプットとして算出します。
これを例えばWindowsでは先に挙げたEqualizer APOで適用し、スピーカーから出る音に適用します。

使い方

以下、プログラムの使い方について簡単にまとめます。

まずはプログラムの入手です。適当なフォルダでプロンプトを開いて以下コマンドを入力するとファイル一式がダウンロードされます（その前にGitをインストールしてない人はしてください）。

git clone https://github.com/quick-waipa/mkEqSFC.git

次に、スピーカーの周波数特性データを作成することが必要です。
これには先に挙げたREWというフリーソフトが使えます。マイクを使って計測して下さい。
ただ、エクスポートデータがそのままの形だと上記プログラムから読めないので、加工が必要です。エクセルなどを用いてカンマ区切りのテキストデータを用意して下さい。データ形式についてはREADMEを参照して下さい。
REWの設定でカンマ区切りでヘッダー等はオフにして出力して下さい。

以下に入力データのサンプルを示します。

20.00, -23.69
21.86, -23.08
21.86, -23.08
22.35, -22.85
22.35, -22.85
22.72, -22.85
22.72, -22.85
...中略...
19669.59, -31.04
19779.11, -31.35
19779.11, -31.35
19889.25, -31.54
20000.00, -31.69
20000.00, -31.69

次に上記「mkEqSFC」を起動します。srcファイル内にて以下コマンドを実行してください（Pythonおよび必要ライブラリをインストールしてない人はしてください。README参照）。

python mkEqSFC.py

以下のようなウィンドウが開くので、インプットデータを入力します。これについてもREADMEに詳細を書きましたので参照して下さい。

「Run Calculate」を実行すると、アウトプットデータとして以下が出力されます。

2種類のイコライザー設定ファイル
RMS算出結果（rms.txt）

2種類のイコライザー設定ファイルとは、上で述べた2種類の音場補正のイコライザー設定です。これを何らかの方法で適用します。
ここでは上で挙げた「Equalizer APO」を使うことを想定します。
Equalizer APOではある音声入力を二つにわけてそれぞれイコライザーを適用し、再びミックスするということが可能です。なので、そのようにして式(10)を実現させます。

ミックスする際、二つに分けた音声の音量をまず調整する必要がありますが、それにはアウトプット結果のRMS算出結果(diff)を利用して下さい。

なお、αに対するゲインの計算式は以下です。

$${Gain_A=6log_2(α)}$$

式(11)

$${Gain_B=6log_2(1-α)}$$

式(12)

αは適当な音楽を聴きながら良さげな値を設定して下さい。αを1に全振りすると曇った、ウォームな、つまらない感じの音になり、逆に0に全振りするとはっきりした、すっきりした音になると思います。いい塩梅を探って下さい。

参考までに、Equalizer APOの設定ファイルのサンプルを以下に示します。

Copy: L2=L R2=R
Channel: R2
Preamp: 1.59 dB # RMS_diffより
Include: "eqフィルターA(R)のパス"
Channel: L2
Preamp: 2.01 dB # RMS_diffより
Include: "eqフィルターA(L)のパス"
Channel: L2 R2
Preamp: -8.99246725597274 dB # =6log_2(α)
Channel: R
Preamp: 1.29 dB # RMS_diffより
Include: "eqフィルターB(R)のパス"
Channel: L
Preamp: 2 dB # RMS_diffより
Include: "eqフィルターB(L)のパス"
Channel: L R
Preamp: -3.780503809425822 dB # =6log_2(1-α)
Copy: L=L+L2 R=R+R2

追記：
スピーカーではなくヘッドホンの補正をする場合は、（ターゲットカーブにハーマンカーブなどを用いるよりも）片方はイコライザーを設定しないで原音とDry/Wetで混ぜる方が上手くいく気がします。
ハーマンカーブでかなり上手くいきました。環境に合わせて使い分けて下さい。

Copy: L2=L R2=R
# Channel: R2  
# Preamp: 1.59 dB # RMS_diffより  
# Include: "eqフィルター１(R)のパス"  
# Channel: L2  
# Preamp: 2.01 dB # RMS_diffより  
# Include: "eqフィルター１(L)のパス"  
Channel: L2 R2
Preamp: -8.99246725597274 dB # =6log_2(α)
Channel: R
Preamp: 1.29 dB # RMS_diffより
Include: "eqフィルター２(R)のパス"
Channel: L
Preamp: 2 dB # RMS_diffより
Include: "eqフィルター２(L)のパス"
Channel: L R
Preamp: -3.780503809425822 dB # =6log_2(1-α)
Copy: L=L+L2 R=R+R2

結果

では、結果はどうなったでしょうか。

結果は、良好です。これまでのように音が曇ったり引っ込んだり音質が劣化したりといった感じはまったくなく、むしろ音がクリアになり、明らかに音質が改善されたように感じました。
正しいかどうかはともかく、式(10)の良さを感じさせる結果となりました。

もしスピーカーの音質に不満があって、かつ音場補正システムとか高くて買えない、というのであれば、このプログラムを試してみるといいかもしれません。

追記（2024/4/21）：
ヘッドフォンの場合、スピーカーの場合ほどは劇的に良くはなりませんでした。理由として、おそらくヘッドフォンの場合は部屋を通さずに直接耳に届くので最初からメーカーの意図通りの音が鳴りやすいのと、個人差が大きい頭部伝達関数の影響をより強く受けるからではないかと考えられます。
あとヘッドフォンはそもそもマイクでの測定が難しいというのもあります。
ヘッドフォンの場合はターゲットの設定等が難しいですがうまくやればちゃんと改善しました。

まとめ

話題のARC STUDIOが高かったのでフリーの音場補正プログラムを使ってみた
が微妙だった
より厳密な音場補正の式を求めた
求めた式より音場補正用イコライジング設定作成プログラムを自作してみた
結果、スピーカーの音質がすごく改善された