03_存在とはなにか
万物の根本原因についてトリレンマに陥らないように考えていった結果、あらゆる恣意性を排したあり⽅、すなわち<すべて>なるものに⾏き着きました。
では、本当にこの<すべて>なるものはトリレンマを避けることができているのでしょうか︖ 前と同じように、以下の問いを考えてみます。
「では、なぜ<すべて>は存在するのか︖」
……しかし、これははたして意味のある問いでしょうか︖
この問いが成⽴するためには、前節で述べたように、<すべて>以外にもなんらかの「在り⽅」の選択肢があり、その中で恣意的に<すべて>というあり⽅が選択されているのでなければなりません。しかし、上でみたように<すべて>はその内部にあらゆる選択肢、すなわちあらゆる「在り⽅」を内包していて、存在として何も「選択」されていないという状態です。だからそもそも<すべて>それ自体を「存在」としてカウントしていいのかどうか、という問題になると思います。
さて、ここで疑問が生じます。
そもそも、「存在」とはいったい何でしょうか︖
そもそものそれが分からなければ、「なぜ<すべて>は存在するのか︖」という問い自体の意味がわからなくなってしまいます。
そこで、今回の内容では「存在とは何か︖」ということをみていき、その定義をはっきりとさせていきたいと思います。
1.「存在」と還元論
ということで、「存在とは何か?」という問いに迫るために、今まさに目の前の机の上にある「このリンゴ(this apple)」について、まずは考えてみたいと思います。
「このリンゴ」は、果たして「存在」なのでしょうか?

……いやいや、リンゴはさすがに存在しているでしょう。
と、素朴には考えるかもしれませんが、よくよく考えてみると、それはそこまで確かな事実とは言えないようにも思えてきます。
たとえば、我々がリンゴを眺めている時に感じる「赤色」という色は、「存在している」と呼べるでしょうか?
その発生メカニズムを考えると、「赤い」ということは、リンゴ表面が反射したある波長域の電磁波を我々が錐体細胞によって電気信号に変換し、脳内で「赤い」というクオリアとしてラベリングして生じたものです。リンゴの「赤い」という特性は、「赤」に相当する波長の電磁波を反射しやすい、というリンゴの表面の物理的特性へと還元できます。
また、「リンゴ」という物質は、還元すれば分子の空間的配列です。そしてさらにミクロレベルに還元していけば、原子、核子、素粒子、等々の配列ということになり、そのようなレベルでみれば、どこからどこまでが「リンゴ」に相当する素粒子なのか、ということは完全にわからなくなってしまいます。なぜなら素粒子論によれば、粒子は場の励起によって生じている一種の「波」であり、同種粒子はそれぞれアイデンティティーをもたず、区別できないからです。
そのように考えてみると、「リンゴ」という存在はその構成要素へと還元していけば完全に胡散霧消してしまうもの、と言えてしまうようです。
では、一旦開き直って、そのような胡散霧消してしまうものはとりあえず「存在」から除外することにしてしまって、とにかくミクロレベルにひたすら還元していった結果、確実に「存在」と呼べそうなものとして残るものは何か? ということを探ってみるという方針ではどうなるでしょうか。
それはまさに、前回の1.節で行ったことに他なりません。
前回の1.節では、ミクロの構造を還元論的にひたすら追い求めていくと、結局「万物の法則」としてなんらかの「要素」と「関係」といったものが残るのではないか、という所にたどり着いたのでした。
では、この「要素」と「関係」が織りなす「万物の法則」こそが「存在」であって、それ以外のあらゆるものは「存在」には該当しない、という結論になるのでしょうか?
……しかし、この結論は無理があると思います。
「『本当に』存在しているのは『自然法則』であって、『このリンゴ』は実は存在していない」、などという主張が正しいとするならば、この世界には自然法則だけがあるはずで、リンゴは存在しないはずです(ミクロレベルでみればどの素粒子が「リンゴ」なのか区別がつかない、ということを考えてみて下さい)。
つまり、ミクロレベルの自然法則の立場からしたら、マクロレベルに現れるあらゆる「モノ」は、存在する必然性が特にないのです。
しかしそれにも関わらず、不可解なことに、明らかにマクロレベルの存在物である原子、分子、細胞、生命、惑星、恒星、……等々は存在しているようにみえます。
目の前のリンゴはやはり主観的事実として、なぜだか知らないけれど、「在る」のです。
この奇妙な事実を説明できないかぎり、すべてを統一的に説明したことにはならないはずです。
やはり「存在」の定義をするにあたり、以上のような還元主義的な方法は、何かが間違っているのではないかと考えられます。
2.「粗視化」と「創発」
前節では、「<すべて>はなぜ存在するのか?」という問いについて考える前に、そもそも「『存在』とは何か?」という問いについて明らかにする必要がある、ということで「存在」の定義についてみていくことにしました。
そして、まずは我々が素朴に「存在」と信じているものを還元論的に構成要素に分解していって「本当に在るのは何か?」ということを考えていった結果、「リンゴは存在しない」というような妙な結論にいたってしまったのでした。
どうやら、「本当の存在」のような狭量な考えでは無理が出てくるようです。そうではなくてむしろ、「このリンゴは存在する」、という常識的な結論を導くような定義付けを考えなければならないと思われます。
ここで、前節でみてきたこととして、注目すべき事があります。
前節では、リンゴを素粒子レベルに分解していった結果、「リンゴ」という存在は胡散霧消してしまったのでした。
レゴブロックをレゴブロック単体としてみている限り、そこに「家」は存在しないように、素粒子を素粒子レベルで見ている限り、そこに「リンゴ」は存在しません。
「リンゴは存在している」と言い張るためには、還元論的に構成要素に分解するようなやり方ではなくて、もっと別の、言ってしまえばまったく逆の方向性の見方が必要になるようです。
つまり、マクロをミクロに分解する見方ではなく、逆にミクロの構成要素からマクロの「存在」を浮かび上がらせるような手続き、あるいは現象です。
そのような現象は、一般には「創発」と呼ばれているようです。
「創発」という言葉が出てきましたが、これは一体どういう概念でしょうか?
Wikipedhiaで調べてみると、以下のように記載されているようです。
創発(そうはつ、英語:emergence)とは、部分の性質の単純な総和にとどまらない性質が、全体として現れることである。
ただこれだけではちょっとわかりにくいので、その本質がなんなのかを少し考えてみたいと思います。
ここで、話を単純にするために、思考実験的な仮定として、この世界はある一つの「万物の法則」に従って動いており、その法則によれば万物の根源的単位は「ヒモ」である、とします。そして我々がこの世界にみているあらゆる物質、力、空間、時間、等々はすべて還元すれば「ヒモ」の振動パターンとして記述することができる、とします(なおこれはあくまで議論のための仮定であり、特定の物理理論とは何の関係もありません)。
ここでは「現実」にあるのはただ、「ヒモ」の振動だけです。
さて、今、目の前に、ひとつのリンゴがあるとします。
その「リンゴ」はあたかも実在しているようですが、前節でやったように構成要素に還元してみれば、そのリンゴは原子、分子、素粒子、電磁気力、核力、空間、等々によって形作られており、さらに還元すると、そこにあるのは無数の「ヒモ」の振動だけです。
にもかかわらず、そこには「リンゴ」が存在するようにみえます。
これは言ってみればたくさんの画素が並んだモニターを遠くから眺めると画像が映し出されているようにみえるようなもので、解像度をうんと下げて「ヒモ」の集まりをみているのであり、別の言葉では「粗視化」とも呼ばれます。
そして、あるパターンを「粗視化」して眺めたとき、元のパターンとは一見関係ないような新たなパターンがマクロレベルで現れ出ているようにみえるとき、それを「創発」と呼びます。
よって、「リンゴ」があたかも存在しているようにみえるのは、「無数の『ヒモ』の振動パターン」というパターンが「粗視化」され、それによって「リンゴ」というパターンが「創発」されたからである、と言うことができます。

ところで話は変わりますが、「宇宙の熱的死」という概念があります。
エントロピー増大則に従うなら、宇宙に存在する物質、星、生命といった秩序だった構造はいずれ存在できなくなり、あとにはただ均質化された無秩序だけが残る、というようなものですが、仮に誰もこの宇宙を粗視化して眺めなかったとしたら、そのような「熱的に死んだ」宇宙は、「熱的に死んでいない、物質や星や生命に溢れた」この宇宙と、実は特に違いがなくなります。
なぜなら粗視化を行わなければ、物質や星や生命といった「眺め方」が存在しないため、何が秩序で何が無秩序かと決める基準もなくなってしまい、よって「無秩序さ」を表すエントロピーは最初から最後まで変化しないからです。

ちなみにWikipedhiaで「粗視化」という項目を調べてみても、以下のような記載があるようです。
一般的によく言われる「エントロピーの増加法則」は、何らかの情報に対して粗視化された分布関数に対して初めて成り立つ。
このことは「時間の矢」というものを考えてみるとよくわかります。
「覆水盆に返らず」という言葉があるように、我々の日常世界のスケールでは、時間は逆行したりせずに一方向に流れ続けるものだと思います。割れたコップが勝手に元に戻ったり、熱いお茶に入れて溶けた氷がひとりでに周りに熱を発散して再び凍り付くようなことは、まず考えられません。
一方で、よりミクロのレベルでみてみると、物理法則は時間対称の形で記述され、時間に方向はありません。分子や素粒子が反応する様子を仮に映像に収めることができたとして、それが普通に再生されたものなのか、それとも逆再生されたものなのかは、映像を見る限りでは判断がつかないのです。 すなわち、「時間の矢」はミクロスケールの現象をマクロスケールに粗視化することによってはじめて成立するのです。
また、別の例をとって考えてみますと、例えばエントロピー増大の法則はよく部屋の汚さと関連づけて説明されますが、これについても、どのような状態を「片付いている」とみなし、どのような状態を「片付いていない」と見なすかは、明らかに恣意的です。猫や昆虫が人間の部屋を眺めたら、たぶんどんな状態であれ大差はないでしょう。それにも関わらず部屋の汚さがエントロピー増大則に従うようにみえるのは、我々人間が部屋の様子をながめてみて、「これは片付いている」「これはごちゃごちゃしている」といったような粗視化を行っているからです。それにより、初めて部屋の汚さはエントロピー増大の法則として説明されるわけです。
以上、「創発」と「粗視化」という概念についてみてみました。この概念を用いれば、「時間の矢」のようにミクロスケールに還元して説明しようとすると胡散霧消してしまうようなマクロスケールの現象について、説明づけることができると思われます。
ということは、むしろいっそのこと、この「粗視化」と「創発」というものを「存在」の定義として採用してみたら上手くいくのではないか、という考えが浮かんできます。すなわち、以下のような「存在」の定義です。
存在
=何かが粗視化され、創発されたもの
……さて、この定義が果たして上手くいくかどうかを確認する前に、まず「粗視化」という概念の定義づけについて、もう少しはっきりさせたいと思います。
とりあえず、「粗視化」という項目をWikipedhiaで引いてみますと、
粗視化(そしか、(英: coarse graining))とは、ある変数空間で定義された連続的な物理量を、その変数を任意の単位スケールで離散化し、単位スケール内で物理量の平均を取ることで、その物理量そのものも離散化し情報量を減らす手法。単純に言うと、モザイクを掛ける事、解像度を下げる事がこれに相当する。
と、なんか書いてありますが、「モザイクを掛ける事」というのが本質だと思います。
ただ、この定義では物理量として数値化できるものに対象が限られていたりと、定義の範囲が若干狭いように思うので、もう少し一般化できないかと考えてみたいと思います。
3.「粗視化」とは何か?
前節では、無味乾燥なミクロスケールの世界から多様な存在物で溢れるこのマクロスケールの世界を浮かび上がらせるための概念として、「粗視化」と「創発」という概念をとりあげ、これを試しに「存在」の定義として採用してみたらどうか、というところまで考えました。
しかししかしその前に、「粗視化」という概念の意味についてもう少しはっきりとさせておく必要があると思われます。この節では「粗視化」のより一般的化された定義について、考えていきたいと思います。
さて、「粗視化」とは何か、ということを改めて確認しますと、それは簡単に言えば「モザイクをかけること」でした。
以下、例を挙げて考えてみます。
まず、以下のような、空間の中に何か粒子のようなものが分布している状態を考えます。

この時、この空間内に含まれる粒子の数を数えることで、粒子の分布はある「密度」として単純化することができます。
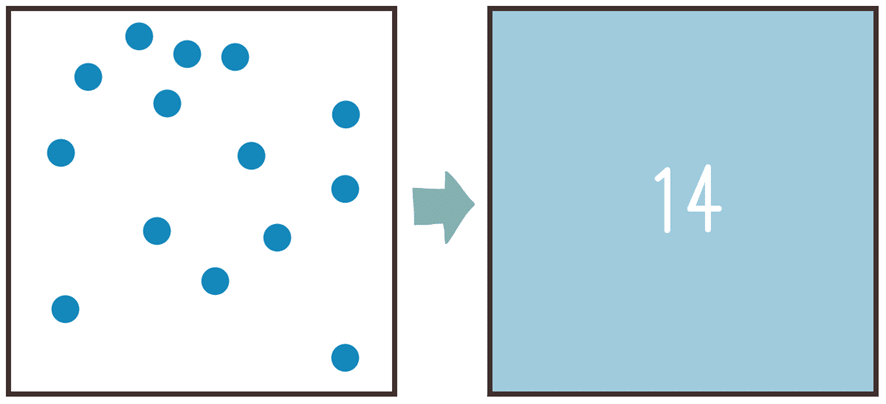
これが「粗視化」の簡単な例です。
ここで、例えば粒子の分布が次のようであっても、

あるいは、つぎのようであっても、

粒子の数が同じであれば、同じように「14」として粗視化されることがわかると思います。
すなわち、「『空間中に多数の分子が分布している状態』をグルーピングして、まとめて『ある密度』としてみなす」ということです。
このように、ある情報をあるやり方でグループ分けして無駄な情報を切り捨て、全体を単純化させること、これが(普通の意味での)「粗視化」です。
さてここで、上の例では密度「14」に対して、「14」という数字が割り当てました。しかし考えてみると、この「14」とかいうものは、一体どこからやって来たのでしょうか?
それはもちろん、他にも「3」とか「25」とか数字があって、その中から「14」に対応する密度の数字が割り当てられた、と考えられます。これは逆に言えば、「14」は、それ単独で成立しているのではなく、「3」とか「25」とか、その他の粗視化の仕方との相対関係によって成立している、ということです。

そのように考えると、先に挙げた「14」に相当する粒子の空間分布は、「3」「14」「25」といった様々なグループ分けがある中から、「14」というグループ分けに相当する粒子の空間分布のグループが「選択」された、ともみなせると思います。
何を言っているか今の段階ではわかりにくいかもしれませんが、要するに、「14」はそれ単独では成立しない以上、それは複数のグループ分けの中から「選択」されたものでなければならない、ということです。
以上を踏まえて、「粗視化」という概念をここでは以下のように一般化したいと思います。
粗視化
=複数の状態をとり得るある対象について、任意のやり方でグループ分けをし、そのうちあるグループが選択されること。
以降、本稿の中で用いる「粗視化」という言葉は、すべて上記の意味で用いることとします。
以下、いくつか例を挙げます。
例1:上でみたように、「単位空間中にN個の粒子がある状態を「密度N」として粗視化して表現する」ということは、『粒子の空間的配置』という対象を「密度3」「密度14」「密度25」等々とグループ分けし、そのうちの一つのグループである「密度14」が選択される、ということを意味します。
例2:「目の前にある分子のかたまりを「りんご」と粗視化して表現する」ということは、『あらゆる分子の空間配列』という対象を「りんご」「みかん」「猫」、等々とグループ分けし、そのうちの一つのグループである「りんご」が選択される、ということを意味します。
例3:「水素原子の周りにある電子雲を観測し、電子の位置を位置ΔXnに確定させる」ということは、『電子がとり得るあらゆる位置』という対象を「位置ΔX1」「位置ΔX2」「位置ΔX3」、等々とグループ分けし、そのうちの一つのグループである「位置ΔXn」が選択される、ということを意味します。
例4:「自然数3」は、『世界中のありとあらゆるものの集まり』という対象を「自然数1」「自然数2」「自然数1000000」、等々と抽象化することによってグループ分けし、そのうちの一つのグループである「自然数3」を選択する、ということで成立しています。
このように、数学的対象やプラトン的なイデアのようなもの、あるいは人間の抽象的思考のようなものも、「粗視化」という枠組みで説明できます。
むしろ、我々が素朴に「存在」と考えているような、あらゆる対象がこの粗視化の定義によって説明づけられることが分かると思います。
ということで、次節では以上みてきた「存在」の定義を用いて、「<すべて>自体は存在と呼べるのか?」という最初の問いについて、解答を与えたいと思います。
4.解答
1.節からここまで、「『存在』とは何か?」という問いについて考えてきました。そして、「粗視化」「創発」といった概念で「存在」を定義し、また「粗視化」という概念についても前節で定義付けを行いました。
あらためて、本稿における「存在」の定義を以下に示します。
存在
=何かが粗視化され、創発されたもの
そして前節でみたように、(本稿における)「粗視化」とは、
粗視化
=複数の状態をとり得るある対象について、任意のやり方でグループ分けをし、そのうちのあるグループが選択されること。
であり、また「創発」とは、あるパターンを「粗視化」して眺めたとき、元のパターンとは一見関係ないような新たなパターンがマクロレベルで現れ出ているようにみえることを言うのでした。
すなわち、そのようなものこそが「存在」です。
以上の定義づけを用いて、今回の問題であった「<すべて>自体は「存在」と呼べるのか?」という問いについて、本節では考えたいと思います。
さて、ところで上のように並べてみると、「存在」の定義にある「何か」とは、すなわち粗視化の定義にある「対象」のことである、ということが分かります。
(「存在」の定義における)何か = (「粗視化」の定義における)対象
つまり、「存在」が成立するためには、粗視化を行う元となる「対象」がまず成立している必要がある、ということです。
ここで、1.節の最初にあげた、「このリンゴ」の存在について考えてみます。
1.節では、還元論的に「このリンゴ」の粗視化をひたすらミクロレベルに解除していった先に最終的に残るものとして、「万物の法則」における「関係」「要素」といったものを考えました。しかし、この「要素」なるものは、果たして「存在」に該当するものなのでしょうか? するとしたら一体何を対象として粗視化したものなのでしょうか?
……いやいや、粗視化をひたすら解除していった先に最終的に残るものなのだから、「要素」自体は何かを粗視化して得られたものではないだろう、とも考えられるかもしれませんが、そのように考えると、「要素」自体は存在ではない、ということになってしまい、ではそれは何処から来たのか? という疑問に答えられなくなってしまいます。
そこで、ここでそもそも、「粗視化をひたすら解除していった先に最終的に残るもの」なるものとは一体全体どんなものなのか、ということを考えてみます。たとえばそれが「0」と「1」のようなものだと考えると、たしかにそれは万物の「要素」っぽい(?)ですが、そのような数学的な対象物が「粗視化」されて作られた存在物であることは前節でも確認した通りです。
では、そのような「数学的な対象物」は、一体何を粗視化して得られたものなのでしょうか?
これは前節の例4にも書いていますが、それはすなわち「この世界のありとあらゆるもののあつまり」であり、別の言葉で言えば「あらゆる可能なあり方」です。
つまり、<すべて>そのものに他なりません。
ここで、今回の問題である「<すべて>自体は存在と呼べるのか?」という問いに、ようやく答えを出したいと思います。
あらためて、<すべて>の定義を以下に示します。
<すべて>
=「『すべてがある』かつ『何かがある』かつ『なにもない』、そのようなありとあらゆる可能性がすべて重なりあって不確定な状態、あるいは構造」
このようにみると、<すべて>とはまさに「あらゆる粗視化を解除していった先に最終的に残るもの」に該当するのではないかと思われます。実際、<すべて>はあらゆる可能なあり方、すなわちあらゆる「対象」及び「存在」をその内に内包していて、何もグループわけも「選択」もされていない状態です。
すなわち、<すべて>自体は「存在」ではないのです。
さらにここで、(伏線として張っておいた)前回の「ミュンヒハウゼンのトリレンマ」の帰結を思い出してください。
前回では、「ミュンヒハウゼンのトリレンマ」は以下の<根源的ループ>へとまとめられる、ということを考えました。
唯一つの真実
原因の循環(=無限後退)構造が無根拠に存在する。
上で述べたように、「あらゆるすべての粗視化を解除していった先に、最終的に<すべて>そのものにたどり着く」、とするならば、まさにこの「原因の循環(=無限後退)構造が無根拠に存在する。」の通りです。
そして<すべて>自体は「あらゆる恣意性を排した唯一のあり方」であるため、メタな理屈を遡ってこの循環構造自体の根拠を問う必要はもうありません。
よってここに、「ミュンヒハウゼンのトリレンマ」は解決されたと考えられます。

つづく
