
Radiomics超入門:Radiomicsの特徴計算までのスキーム
Radiomicsの特徴計算スキーム概要
Radiomicsでは、画像特徴を計算するための下準備の意味を含んだ、画像処理(image processing)のスキーム(図1)に沿って処理が行われます。
ここでいう画像処理というのは、データ変換、ポストプロセッシング、セグメンテーションやレジストレーション、画像補間(画素補間)、マスク作成などを指します。これらの処理を経て、ようやく、画像特徴の計算を行うための準備が整います。
一見、複雑なように思えますが、Radiomicsを計算するためのソフトウェアは、このような画像処理が自動で処理できるように設計されていることがほとんどです。1から自分でデータやプログラムを作ることは多くの場合不要です。
図1に、画像処理の流れ(スキーム)を示します。
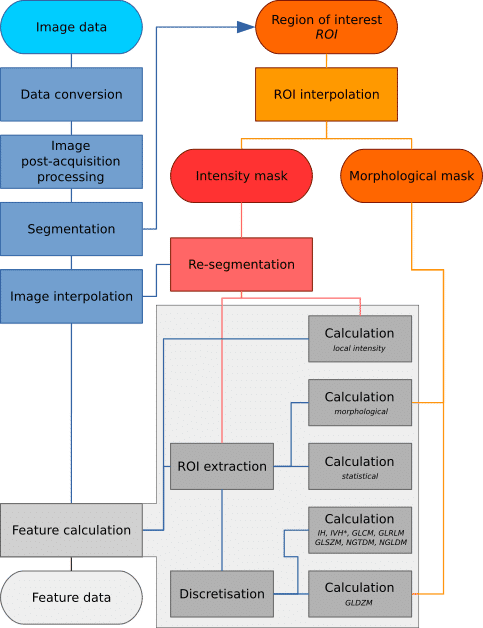
Adapted from the Section Image processing, Fig. 1, IBSI ref.
以降、この図に示されている各項目について解説していきます。
Image data(画像データ)
デジタルな画像データ全般を意味します。レントゲン、マンモグラフィー、CT、MRI、超音波、SPECT、PET、病理切片などの顕微鏡画像などがよく用いられます。
Data conversion(データ変換)
画像によっては、生画像データをより意味のあるピクセル値を持つ画像に変換する必要がある場合があります。例えば、PET画像なら、Standard Uptake Value(SUV)[Boellaard2015] に変換する場合などです。何らかの指標やパラメータを画像化したパラメトリック画像や、計算画像もこのような変換が必要な画像と言えるでしょう。画像の変換については、モダリティ(イメージング機器・装置)に依存します。この依存に関する影響は各装置の特性ごとに異なり、本解説の範疇を超えますので、詳細は割愛させていただきます。
Image post-acquisition processing(画像後処理)
画像は、画質を向上させるために後処理されることがあります。例えば、MRI画像にはガウスノイズ、Ricianノイズ、Rayleighノイズが含まれており[Gudbjartsson1995]、ノイズ除去を行うことで画質の向上を試みることができます。別の例として、MRIを使用して測定されたボクセル信号強度は、画像全体で不均一である可能性があり、補正が必要な場合があります[Sled1998][Vovk2007][Balafar2010]。FDG-PETベースでは、さらに部分容積効果(パーシャルボリューム効果)[Soret2007][Boussion2009]やノイズ[LePogam2013][ElNaqa2017]の補正が必要な場合があります。CT画像では、ペースメーカーや歯のインプラントなどの金属物がアーチファクトを引き起こすため、アーチファクト抑制が必要になることがあります[Gjesteby2016]。顕微鏡画像は、光源や光路によって照明が不均一になるため、視野照明補正が有効であることが知られています[Caicedo2017][Smith2015]。
画像取得後の処理方法(ポストプロセス)の標準化は、本解説の範囲外です。画像再構成時にノイズ除去やその他の後処理を行うソフトウェアをベンダーが提供または実装しているので、これに頼りましょう。ベンダーがこのような機能をルーティーンで自動化している場合で、画像後処理に特別な研究要素がない場合は、追加の画像後処理は必要ない場合がほとんどでしょう。
この他、レジストレーション(画像の位置合わせ)が前処理として必要な場合があります。例えば、時系列に取得した同じ性質の画像を、画像上で同じ位置にしてから解析したい場合や、MRIのシリーズ画像のように、同一検査ではあるものの、異なる時間軸で得られた画像をなるべく同じ画像上の位置で解析したいという場合に行われます。
Segmentation(関心領域の作成)
処理や解析の対象となる領域を関心領域(Region Of Interest, ROI)と呼びます(図5左上)。画像特徴の計算は、ROIの定義に依存しています。ROIは特徴を計算する領域を定義するために使用されるためです。何がROIとして捉えられるか(どの領域をROIとするか)は、研究目的によって異なります。例えば、細胞プレートの3D顕微鏡検査では、画像上に写る細胞がROIとして扱われます。癌を捉えるために取得された医療画像では、腫瘍をROIとして扱うのが一般的です。ROIは専門家が手動で定義することも、アルゴリズムを使用して(半)自動で定義することもできます。
プロセスの観点からは、セグメンテーションはマスク画像の作成を行うためのものと説明できます。具体的には、ROI $${R}$$のうち、$${j}$$の位置にある領域の集合を $${R_j}$$ と定義します。
$$
R_j = \begin{cases}
1 &\text{} j in ROI \\
0 &\text{} otherwise
\end{cases}
$$
ROI は通常、画像とペアで保存されます。一部の画像フォーマット(NIfTI、NRRD、DICOM Segmentation など)は、ROIマスク画像(ROIの領域を任意の値に、その他を0としたバイナリ画像)を直接保存できます。また、DICOM RTSTRUCT や DICOM SR ファイルのように、ROI がポリゴンのClosedなループを定義する $${(x,y,z)}$$ 座標点の集合として保存される場合もあります。このような場合、ROI マスクを生成するために、座標に応じた輪郭ポリゴンを再構築して、輪郭ポリゴンに囲まれた空間内にあるボクセルを$${R_j}$$として決定する必要があります。
画像スライス内の点が2D上のポリゴンの内側にあるかどうかを判定するのは、交差数アルゴリズムで決められます [Schirra2008]。Even-Oddルールによるアルゴリズムの簡単な例を図2に示します。

(黄点はボクセル中心位置を示す。緑点はROIエッジとRayとの交点、青点はポリゴンの辺に囲まれた(ROIエッジとRayとの交点に囲まれた)マスクとなるボクセル中心)
Adapted from the Section Image processing, Fig. 2, IBSI ref.
この例では、ROIマスクが規則的なグリッドに並んでいる画像から作成されることが前提になっています。グリッドがピクセルに見えますが、そうではなく、黄色や青色のグリッドの交点がピクセルの中心を表していることに注意してください。
まず、ポリゴンの外側から、各行でRay(走査線)を走らせます(実際には、行でX軸方向に順次ピクセルを処理していく)。
そのときに、走査線とポリゴンのエッジとの交点を定めます(図2-2,3 緑点)。そして、その交点の内側に位置するピクセルをROIマスクとして扱います。
この例では、Even-Odd ルールという方法でROIマスクを決めています。このルールは、走査線を左から走らせて、ポリゴンのエッジを通過するごとに1を足す操作をします。最終的に、走査線の各列の値が奇数だった位置のピクセルをマスクとして採用するというものです(図2-3)。
医用向けの解析ではほとんど見かけませんが、より複雑なポリゴンが用いられる場合には注意が必要です。例えば、図3のように、領域が重なるようなポリゴンの場合、重なっている領域がマスクになるのかどうかは、このルールを変更すると変わります。実際には、このような複雑なポリゴンは用いられないので、Even-Odd ルールを基本としていれば問題ないでしょう。

Even–Odd ルール (左下),Non-Zero Winding ルール (右)
Image interpolation(画像補間)
テクスチャから計算される画像特徴は、回転不変を保つために、等方ボクセル補間処理された画像データから計算されることが望ましいと考えられています。これにより、ボクセルサイズを一定にすることができ、異なるデータセット間の比較が容易になります。
ボクセル補間は、ほとんどの画像特徴がボクセルサイズの変化に敏感であるために、画像特徴値に影響を与えます[Yan2015][Bailly2016][Altazi2017][Shafiq-ul-Hassan2017][Shiri2017]。したがって、異なる測定や装置間で一貫した等方性のボクセル間隔を維持することは、再現性のために重要です。
等方ボクセル補間は、ボクセルの$${x, y, z}$$のサイズを統一する処理ですので、そのサイズを実際のサイズから小さくすることも、大きくすることもできます。前者はアップサンプリング、後者はダウンサンプリングと呼ばれます。現時点ではこれらのどちらが望ましいかという明確な指標はありません。
例えば、$${1.0×1.0×3.0mm^3}$$のボクセル間隔のスライスの画像スタック(ボリュームデータ)を考えてみましょう。$${1.0×1.0×1.0mm^3}$$へのアップサンプリングは、実際には存在しないボクセル情報を推論することで補間しなければならないことになります。一方、$${x, y, z}$$ のうちの最大のサイズ$${3.0×3.0×3.0mm^3}$$へのダウンサンプリングは情報損失を引き起こすことになります。
ボクセルサイズを複数設定して、目的変数との関係を比較するマルチ・スケーリング・ストラテジーは、良いトレードオフを提供する可能性があります[Vallières2017]。ダウンサンプリングは画像のエイリアシング・アーチファクト(人工的な周波数成分による画像上のアーチファクト)を引き起こす可能性があることに注意が必要とされています。そのため、ダウンサンプリングでは、その前にアンチエイリアシングフィルターが必要になる場合があります[Mackin2017][Zwanenburg2018]。
一般的に3D画像の補間には3D補間アルゴリズムが用いられますが、状況によっては、3Dであっても、画像スライス面内で完結する2D補間が推奨されることもあります。2D補間では、ボクセルはスライス間(スライス方向)で補間されませんから、これが利点になることがあるのです。例えば、スライス間隔が所望のボクセルサイズに比べて大きい場合、または、面内間隔に比べて大きい場合に有益である場合があります。しかしやはり、2D補間の欠点は、ボクセルが等方でなくなることです。その結果、画像特徴は面内のみで計算するという制約を強いられます(言い換えると、3Dテクスチャ特徴の計算には不向きということです)。
ボクセル補間アルゴリズムの種類によって、補間後の画像の変化の仕方が変わります。[Larue2017]はファントム研究において、最近傍補間(Nearest Neighbor)、トライリニア補間(Trilinear)、トライキュービック補間(Tricubic)を比較し、特徴の再現性は選択された補間アルゴリズムに依存すること、すなわち、ある特定のアルゴリズムに統一することでより再現性の高い特徴が得られることを示しています。
画像補間の際、画像の各ボクセルの信号強度は、補間計算後の丸めや、カットオフ値の適用が必要な場合があります。例えば、CT画像の信号値はHU単位で表わされ、整数以外の値をとりません。ボクセル補間後、補間されたCT値(HU値)は四捨五入、あるいは小数点以下切り捨てなどで、整数に丸められます。
ROI マスクを定義済みの画像が補間によって変更された場合、ROIマスクも同じ寸法に補間(ROI interpolation)されなければならないことに注意しましょう。ROIマスクの補間は、最近傍補間またはトライリニア補間を使用するのが一般的です。ROIマスクのトライリニア補間は、部分容積効果を生じさせるため、一部のボクセルが元のボクセルの一部分を含む(あるいは削られる)ことになります。最近傍補間では、ROIマスクは部分容積効果の影響を受けないので、補間後のマスクを直接使用することができます。
では、ROIをトライリニア補間した場合はどうするかというと、ROIマスクは2値マスク(本解説では 0 or 1で構成されるマスク画像)であるため、部分容積効果の閾値$${\delta}$$(デルタ)を設定することで、そのような部分容積で生じた中途半端な値を持つボクセルを2値化します。
$$
R_j = \begin{cases}
1 &\text{}R_{interp,j}≥δ\\
0 &\text{}R_{interp,j}<δ
\end{cases}
$$
部分容積の閾値として一般的に選択される値はδ=0.5です。例えば、トライリニア補間後に0.66になったボクセルがあった場合、δを0.5に設定していれば、マスク領域(1)として扱うということになります。
Interpolation grid(画像補間後のグリッド座標)
画像補間により、補間されたボクセルの中心は、規則的に行列で配置されています。ここでは、グリッドの交点がボクセルの中心として考えます。
グリッドの交点は 2 つの座標系で表されます。
1 つ目の座標系はグリッド座標系で、原点が (0.0,0.0,0.0) で、直接近接するボクセル中心間の間隔は 1.0 です。グリッド座標系は、コンピュータによって、ひいては補間アルゴリズムによって通常用いられる座標系です。
2番目の座標系はワールド座標系です。これは医用画像処理で一般的に用いられるもので、mmなどの距離単位スケールでキャリブレーションされた空間を提供します。
画像補間を行うとき、画像のマトリクスサイズが変わる場合、これらの座標系が一致するように変換する必要があります。このような変換には少しコツが必要です。
図4に、3つの一般的なグリッド配置法を示します。

Adapted from the Section Image processing, Fig. 3, IBSI ref.
オリジナルグリッドに合わせる:Fit to original grid
グリッドの交点にあるボクセル中心が元のグリッドの頂点と重なるように補間グリッドが変形されます(図4右上)。
まず、元の画像のサイズを計算してみます。元の$${4×4}$$グリッドのボクセル間隔が$${(3.00,3.00) mm}$$ですから、ワールド座標で元のボクセルグリッドの範囲を計算すると、$${((4-1) × 3.00, ((4-1) × 3.00)=(9.00,9.00) mm}$$となります。この例では、辺の数で計算することに注意してください。
では、これを希望の補間間隔$${(2.00,2.00)mm}$$へ補間したらどうなるでしょうか。結論から言うと、補間されたグリッドは、元のグリッドに正確にフィットしません。最もフィットするグリッドを探そうとすると、$${(9.00/2.00,9.00/2.00)=(4.50+1, 4.50+1)}$$の割り切れない辺の数を持つグリッドになってしまうためです。グリッドの辺の数は整数にしなければならないため、このまま切り上げて$${6×6}$$グリッドにしたとします。その結果、元のグリッドとズレの無いようにFitさせるには、ワールド座標でのグリッド間隔は$${(9/(6-1), 9/(6-1))=(1.80,1.80)mm}$$となります。これは最初に希望したグリッド間隔$${(2.00,2.00) mm}$$とは異なってしまいますが、ボクセルを$${(1.80,1.80)mm}$$とすることで、それぞれの座標系がぴったり当てはまることになります。
しかし、どうしても希望のグリッド間隔あるいはボクセルサイズで計算しなければならない時があるかもしれません。そのようなときは、次の 2 つの方法から選択します。
グリッドの原点を揃える:Align grid origins
希望のグリッド間隔を保つ簡単な方法は、補間グリッドと元のグリッドの原点を揃えることです。図4左下の例でみていくと、補間グリッドは$${(6×6)}$$で、グリッド間隔はワールド座標で$${(2.00,2.00) mm}$$になっています。定義上、両方のグリッドは原点である$${(0.00,0.00)}$$で整列されます。実際には各座標系は少しずれているのですが、これを承知で、計算を行うということになります。
DICOM画像であれば、DICOMのRCS空間(ワールド座標系)で画像の原点座標が記録されています。ワールド座標系の原点を合わせるには、この属性情報を利用することになります。
グリッドの中心を揃える:Align grid center
両方のグリッドをグリッド中心に揃えます。この方法はグリッドの原点を揃える Align grid originsによる方法よりも推奨されています。図4の右下例で、補間グリッドは$${(6×6)}$$です。その結果、グリッド間隔はワールド座標で $${(2.00,2.00) mm}$$となります。
Re-segmentation
Segmentationの結果得られたROI(図5左上)から、さらに抽出条件を絞って領域を再計算する処理をRe-segmentation(再セグメンテーション)(図5右下)と呼びます。
従来から、ROIは 1 つのマスクで構成されてきました。ただし、再セグメンテーションによって内部のボクセルが除外されたり、ROIがサブ領域にさらに分割されたりすることができます。
便宜上、オリジナルの形態的(モルフォロジカル)なROIと、なんらかの条件で再セグメンテーションされたROIとを区別するために、IBSIでは2つのROIマスクの意味をそれぞれ定義しています。
モルフォロジカルマスク(形態学的マスク)
再セグメンテーションの元になるROIです。処理中に変更されることはありません。専門家や(半)自動セグメンテーションアルゴリズムによって定義されたオリジナルの形状を維持したまま処理されます。
インテンシティマスク(信号強度マスク)
再セグメンテーションが可能、あるいは、再セグメンテーションされたマスクで、モルフォロジカルマスク内から抽出条件に従って選択されたボクセルのみを含みます。
画像特徴の多くは、これらのいずれかを用いれば計算できますが、一部、これらの両方が必要なものもあります。モルフォロジカル特徴や、グレーレベルディスタンスゾーンマトリックス(GLDZM)特徴の計算では両方が必要になります。
2次元マスクの模式的な例を図5に示します。

(1) 元の関心領域(ROI)をピクセル強度で示す。 (2) その後、ROIは[1,6]の範囲の値のみを含むように再セグメンテーションされている。この範囲外のピクセルはマスクから除去されるため、水色でマークされている。(3a) オリジナルのROIから変更されないモルフォロジカルマスク。 (3b) (2)で再セグメンテーションされた強度マスク。
Adapted from the Section Image processing, Fig. 4, IBSI ref.
図6にCT画像を基にセグメンテーションした例を示します。図6左上がオリジナルのマスク(モルフォロジカルマスク)です。このオリジナルのマスク領域(青)を 3 つの異なる再分割パラメータを使用して別のマスク(オレンジ,信号強度マスク)を作成しています。右上のオレンジのマスクは、青色マスク内から、CT値の範囲を $${[ -50, 50 ]}$$ に絞ったものです。左下は、青色マスクから標準偏差を計算し、$${ 1.0 × Sigma }$$内のピクセルのみをオレンジマスクとしています。右下は信号の範囲と外れ値の除外を組み合わせて再分割しているもので、他の2例のオレンジマスクが共有して重なる領域になっています。

Adapted from the Section Image processing, Fig. 5, IBSI ref.
信号強度の範囲の決め方・考え方
図5,6 では、指定された範囲外のボクセルを信号強度マスクから除外する例を示しました。より具体的なモチベーションを挙げるとすれば、例えば、CT画像内の腫瘍ROI内の空気や骨組織を示すCT値を有するボクセルや、PET画像内の低活性領域を除外することなどが挙げられます。CTやPETは、ボクセルの信号強度が較正(calibrated)されている画像モダリティのわかりやすい例です。ボクセル強度の範囲は、通常、両側の区間 [a(min),b(max)] または、最小値側を指定した片側の区間 [a,∞] として設定されます。
生のMRIデータや顕微鏡画像などの較正されていない(arbitrary)、任意の信号強度単位の画像の場合は、標準化や較正を行わない限り、ボクセル信号強度をデータ共通の範囲を決める値として設定することが難しいため、再セグメンテーションは推奨されません。
再セグメンテーションで範囲を用いる場合、信号強度のキャリブレーションの有無(例えば、CT値)、離散化アルゴリズムの組み合わせを加味する必要があります(表1参照)。
外れ値のフィルタリング
図5,6で示したように、外れ値の信号強度を持つROI内のボクセルを除外したい場合は、外れ値を定義して、除外します。方法[Collewet2004][Vallières2015]の1つを紹介します。
平均$${μ}$$ と標準偏差$${σ}$$ を使う方法です。$${[μ-3σ,μ+3σ]}$$の範囲外のボクセルを信号強度マスクから除外します。3σを2σなどに調整すると、より厳しく外れ値が制限されます。
ROI extraction(マスキング画像を作成)
画像特徴の多くは、その計算において、 ROI内に対応する画像上のボクセルが、ROI外のボクセルと区別される必要があります。除外されたボクセルは一般的にプレースホルダー値(多くの場合NaN)に置き換えられます。このプレースホルダー値を用いることで、これらのボクセルを計算中に検知して、除外することができます。ROIマスク(ROI画像)に対応するボクセルは元のボクセル強度を維持します。例を図7に示します。

(黒い領域はNaNなピクセル)
Adapted from the Section Image processing, Fig. 6, IBSI ref.
この処理は必須ではないのですが、処理をわかりやすくするためにあえて前処理でこのようにオリジナル画像からROI領域のみを抽出した画像を作成して、この画像を特徴計算の入力に用いることができます。
Discretisation(離散化処理)
ROI内のボクセル強度の離散化または定量化は、テクスチャ特徴の計算を扱いやすくするために必要とされ[Yip2016]、同様にノイズ抑制効果もあります。離散化の例を図8に示します。

固定区間数法(Fixed Bin Number)の離散化では、ビン数が直接の階調度となり、離散化画像の信号強度が決定される。image AとBのように異なる画像であっても、画像のコントラストはビン数に合わせて同質化される。固定区間幅法(Fixed Bin Size)の離散化では、image AとBのオリジナルのコントラストの違いはそのまま残る。ビン幅を大きくすればするほど階調数が減るため、離散化画像のコントラストの粗さが増す。
Adapted from the Section Image processing, Fig. 7, IBSI ref.
離散化には2つのアプローチが一般的に用いられています。
1つ目は固定区間数法(Fixed Bin Number, FBN)による離散化、もうひとつは固定区間幅法(Fixed Bin Size, FBS)による離散化です。ここでいう「区間」とは、ヒストグラムで使われる「ビン」のことで、これはヒストグラム上の縦棒を意味します。最下位のビンは常に値 1 (最小のビン数)であり、0 にはしません。これは、グレーレベル 0 が許されない特徴もあるテクスチャ特徴の計算の一貫性を確保するためです。
これらの 2 つのアプローチは、どちらか好きな方を自由に使えばよいということはなく、適切に選択する必要があります。
Fixed Bin Number(固定区間数法による離散化:FBN)
固定区間数法では、強度$${X_{gl}}$$は固定ビン数 $${N_{g}}$$ に離散化されます。これは次のように定義されます。
$$
X_{d,k} = \begin{cases}
\lfloor{N_g\frac {X_{gl, k}-X_{gl, min}} {X_{gl, max}-X_{gl, min}}}\rfloor + 1 &\text{if }X_{gl,k} < X_{gl, max} \\
N_g &\text{if }X_{gl,k}=X_{gl, max}
\end{cases}
$$
つまり、あるROI内のボクセル$${k}$$の信号強度$${X_{gl,k}}$$は、ROI内で最も低い信号強度$${X_{gl,min}}$$で較正され、その後、区間幅$${(X_{gl,max}-X_{gl,min})/N_g}$$ で除算され、最も近い整数に切り捨てられます(floor関数)。
固定区間数法は、オリジナルの画像の信号強度が、生理学的意味を持っていた場合であっても、その関係を断ち切ってもいいと割り切って解析するときに使います。しかし、画像の信号強度単位が任意(arbitary)であったり、単に見た目のコントラストが重要視される場合には、正規化効果として働き、有用です。さらに、画像特徴量の多くは、与えられたROI内のグレーレベル数に依存するため、固定区間数離散化アルゴリズムを使用することで、複数のROI(例えば、異なるサンプル間)で特徴量の値を直接比較することができます。
Fixed Bin Size(固定区間幅による離散化:FBS)
固定区間幅法は、オリジナルの強度スケールとの直接的な関係を維持できるという利点があり、これはPETのようなモダリティに有用です。
固定区間幅の離散化は、概念的に単純です。新しい区間(ビン)は、幅 $${w_b}$$ の信号強度の区間ごとに割り当てられます。すなわち、$${w_b}$$はビンの幅です。
基本的に、与えられた最小値$${X_{gl,min}}$$から最初の区間が割り当てられます。この最初の区間を決めるための最小値は、任意に決めることができます。FBSで推奨される方法は、再セグメンテーション範囲の下限としてユーザー設定された下限値を最小値とする方法です。あるいは、こちらは非推奨ですが、ROI内の最小信号強度$${X_{gl,min}=min(X_{gl})}$$によって定義される最小値でもよいです。後者の場合、画像ごとに最小値が変動します。ただし、サンプル間の一貫性を保つために、再セグメンテーションの信号強度範囲の下限値のように、すべてのサンプルで常に同じ最小値が設定されることが強く推奨されています(例:CTのHUは-500、PETのSUVは0など)。
信号強度の単位が任意であるために再セグメンテーション範囲が定義できない場合、例えば生のMRIデータなどでは、固定区間幅による離散化アルゴリズムの使用は推奨されていません(表1参照)。
離散化は次のように計算されます。
$$
X_{d,k} = \lfloor{\frac {X_{gl, k}-X_{gl, min}} {w_b}}\rfloor + 1
$$
最小値$${X_{gl,min}}$$ が、ボクセル k の信号強度$${X_{gl,k}}$$ から差し引かれた後、ビン幅$${w_b}$$で除算され、最も近い整数に切り捨てられます(floor関数)。最後に1が加算され、離散化された信号強度として扱われます。
その他の離散化手法
離散化のための方法には多くのバリエーションが存在します。本解説ではFBN、FBSに則った離散化のみを対象とするため、これ以外の離散化については解説しません。[Vallières2015]は、離散化のための強度ヒストグラム均等化とLloyd-Maxアルゴリズムを用いる方法を述べていいます。強度ヒストグラム均等化では、結果として得られるビンが同じような数のボクセルを含むようにボクセル強度を再分配します[Hall1971]。画像のボクセル強度のヒストグラム均等化は、他の離散化アルゴリズム(FBN、FSBなど)の前に実行することができ、また均等化されるヒストグラムのビン数を定義する必要があります。Lloyd-Maxアルゴリズムは、平均二乗離散化誤差を最小化しようとする反復クラスタリング法でヒストグラムを構築します[Max1960][Lloyd1982]。
離散化の推奨事項
画像特徴計算結果の再現性を最適化する離散化手法は画像モダリティに依存します。画像モダリティごとに画像の信号強度の意味が異なるためです。
画像モダリティに合わせて、再セグメンテーションの信号強度範囲、離散化アルゴリズムの可能な組み合わせを選択するために、推奨される使用法を表1に示します。
$$
表 1 異なる画像信号キャリブレーション・再セグメンテーション範囲・離散化アルゴリズムの可能な組み合わせの推奨\\
\begin{array}{|c|c|c|c|} \hline
Imaging Intensity Units^{(1)} & Re-Segmentation Range & FBN^{(2)} & FBS^{(3)} \\ \hline
calibrated & [ a , b ] & ✔ & ✔ \\ \hline
calibrated & [ a , \infin ] & ✔ & ✔ \\ \hline
calibrated & none & ✔ & × \\ \hline
arbitary & none & ✔ & ×\\ \hline
\end{array}\\
* a : range min, b : range max
$$
チェックマーク(✔)は範囲の決め方と離散化アルゴリズムとの推奨される組み合わせを表し、クロスマーク(✕)は推奨されない組み合わせを表しています。
(1) PETとCTは信号強度単位(それぞれSUVとHUなど)が較正された画像モダリティの例であり、Imageing Intensity Unitsは"calibrated"です。一方で、生のMRIデータは任意の強度単位であるため、"arbitrary"です。
(2) 固定区間数(FBN)離散化は、(定義されている場合は)再セグメンテーション範囲そのものではなく、処理に利用されるROI内の実際の信号強度範囲を使用することが推奨されています。
(3) 固定区間幅(FBS)離散化は、最小値の設定値として、再セグメンテーション範囲の下限を使用することが推奨されています。
再セグメンテーション範囲が定義されていない、任意の信号強度単位で定義できない場合(表 1 中 $${none}$$)、FBSアルゴリズムの使用は推奨されません。
離散化アルゴリズムの選択は、信号強度分布、特徴量計算、再現性に大きな影響を与えることが報告されています[Hatt2015][Leijenaar2015a][vanVelden2016][Desseroit2017][Hatt2016][Shafiq-ul-Hassan2017][Altazi2017]。
Feature calculation(特徴計算)
特徴計算はROI内の特徴を定量化する最終ステップです。計算後、特徴量は、興味のある生理学的・医学的結果と関連付けることで、画像バイオマーカーとして使用できます。
特徴の計算時は、それぞれの画像特徴によって作法があります。改めて、図1を見ると、計算する特徴の種類によって、処理のフローが分かれており、離散化の有無なども異なっていることがわかります。特徴計算の詳細については、特徴計算の解説を参照してください。
画像処理パラメータを適切に扱うことは、画像特徴がROIの特徴をより良く定量化することに繋がります。例えば、離散化処理におけるグレーレベルの数が少ない(例えば8または16)ほど、グレーレベルサイズゾーンマトリックス(GLSZM)特徴を使用してROIのサブ領域をよりよく特徴付けることができる可能性があります。一方、GLCM特徴は、グレーレベルの数が多い(例えば32または64)ほど、よりよくパターンを一般化できるかもしれません。テクスチャ解析前の画像補間と離散化の最適化という特定のケースについて、Vallièresら[Vallières2015]はこのプロセスをテクスチャ最適化と名付けています。テクスチャ最適化プロセスが、その後の特徴の予後予測能力に大きな影響を与える可能性があることも示唆しています。別の研究[Vallières2017]では、5つの等方性解像度での画像補間、特定の画像特徴に対する2つの異なるアルゴリズム、FBN離散化のための4つのグレーレベルを条件に、すべての組み合わせを試し、PET画像とCT画像から計算されたテクスチャを使用して最良の予測モデルを探索的に構築しています。
以上、画像特徴と言う名の画像バイオマーカー候補を計算するために必要なスキームについて解説しました。
RadiomicsJの引用はこちら
Kobayashi, T. RadiomicsJ: a library to compute radiomic features. Radiol Phys Technol 15, 255–263 (2022). https://doi.org/10.1007/s12194-022-00664-4
RadiomicsJのリンク
https://github.com/tatsunidas/RadiomicsJ
Stay visionary
