Radiomics超入門：Gray Level Size Zone Matrix特徴

2023年9月22日 06:33

概要

Gray Level Size Zone Matrix (GLSZM) は、繋がっているボクセルのグループ（ゾーン）の数をカウントすることで得られる行列です[Thibault2014]。

隣接するボクセルが同一のグレーレベルを持つ場合、ボクセルは繋がっているものとして扱われます。ボクセルが繋がりのあるグループ（ゾーン）として分類されるかどうかは、近傍の定義によります。テクスチャ解析の3次元アプローチでは、中心ボクセルから、26 個の近傍ボクセルに同じグレーレベルを持つボクセルがないかを探索します。2次元のアプローチでは、8近傍が使用されます。

2次元アプローチにおける既知の問題は、スライスをまたいで連結することで同じゾーンに属すると考えられるボクセルが、スライス面ごとに2つ以上の別々のゾーンとして扱われてしまうことです。しかし、この問題が、GLSZMに基づく特徴量の予測性能や再現性に悪影響を及ぼすかどうかは未解明です。

数式化して解説します。

GLSZMを$${M}$$とします。$${M}$$は、$${N_g \times N_z }$$な行列です。

$${N_g}$$は ROI 信号強度マスクに存在する離散化されたグレーレベルの数、$${N_z}$$はボクセルグループの最大ゾーンサイズです。

$${M}$$の要素$${s_{ij}}$$は離散化されたグレーレベル$${i}$$におけるゾーンサイズ$${j}$$ごとのカウント数です。

さらに、特徴の計算に用いる$${N_v}$$は、ROI 信号強度マスク内のボクセル数を表し、$${N_s=\sum_{i=1}^{N_g} \sum_{j=1}^{N_z}s_{ij}}$$をゾーンの総数とします。

周囲和（Marginal sum）も同様に定義できます。$${s_{i.}=\sum_{j=1}^{N_z}s_{ij}}$$は、グレーレベル$${i}$$のゾーンの数、同様に、$${s_{.j}=\sum_{i=1}^{N_g}s_{ij}}$$は、サイズ$${j}$$のゾーンの数です。

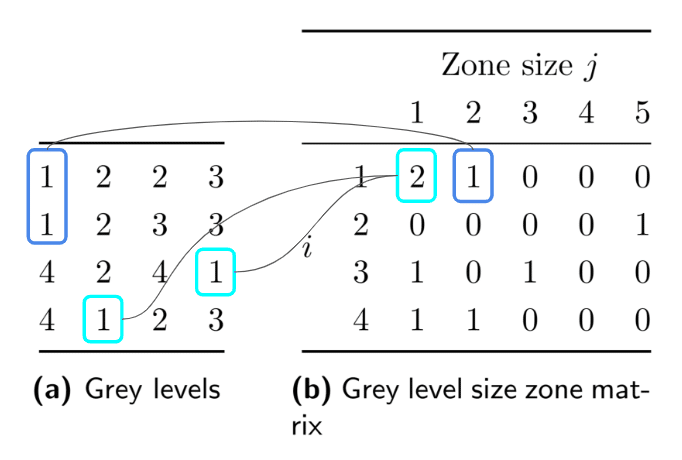
2 次元の計算例を示します。

GLSZM計算例
(a) 元画像 (b) GLSZM - 8 近傍探索 -
（i : グレーレベル，j : ゾーンサイズ）
Addapted from IBSI ref Fig.15

例えば、下の図のように、元画像(a)内のグレーレベル「1」に着目したとき、左上、下側、右側に位置していることがわかります。それぞれ、ゾーンサイズは左上「2」、下側「1」、右側「1」です。よって、GLSZMには、ゾーンサイズ 1 が 2 つ、ゾーンサイズ 2 が 1 つ、となっています。

特徴の集約

GLCMやGLRLMと違って、GLSZMは方向ベクトルごとに計算結果を得るわけではないため、集約の方法は次の 3 つになります。

特徴量の集約の方法
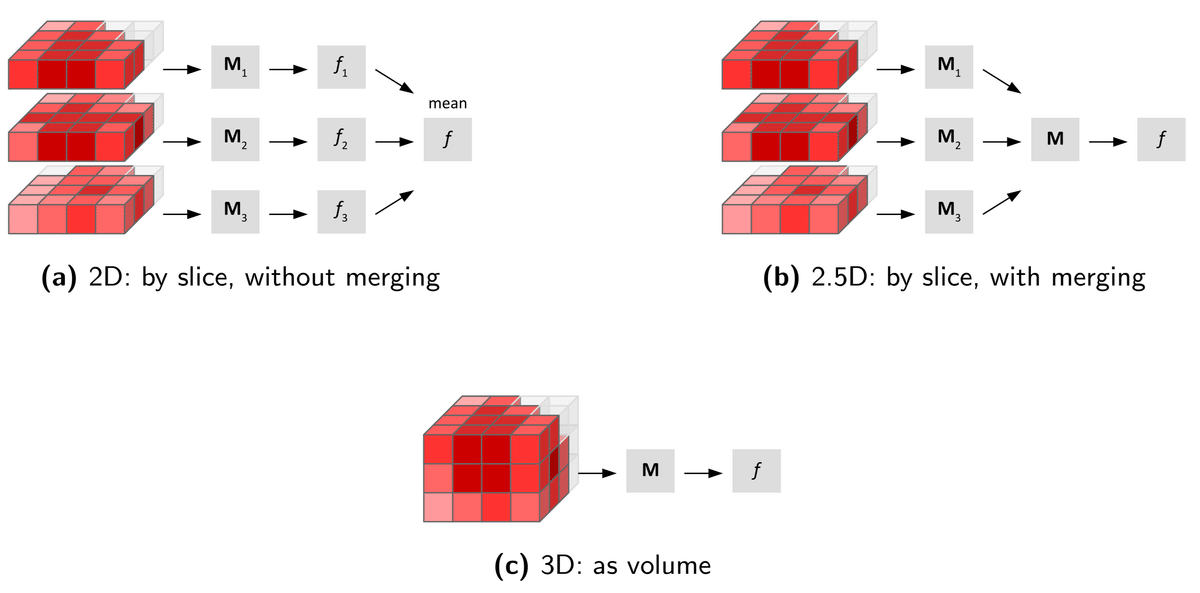
Addapted from IBSI ref Fig. 16

( a ) 2D でスライスごとに特徴を計算したあと平均する
( b ) 2D でスライスごとにマトリクスを計算したあとにマージ（マトリクスを積算）し、マージされたマトリクスから特徴を算出する
( c ) 3D でマトリクスを得て、特徴を計算する

近傍を探索する距離

GLSZMのデフォルト近傍領域は、チェビシェフ距離δ=1 の領域です。

理論上、マンハッタンノルムやユークリッドノルムを用いて近傍領域を定義することもできます。この場合は、どちらも 6 - conected（3D）、4 - connected（2D）の近傍領域になります。

領域の探索距離を大きくすることは技術的には可能ですが、同じ信号強度を持つ別々のゾーンが同じゾーンに属するとみなされるようなケースでは、ゾーンの分類が難しくなります。

GLSZM特徴

GLSZM特徴量の定義は、GLRLM特徴量 [Thibault2014]の定義に基づいています。

Small zone emphasis

小さなゾーンを強調する特徴です。

$$
F_{szm.sze} = \frac {1} {N_s} \displaystyle\sum_{j=1}^{N_z} \frac {s_{.j}}{j^2}
$$

Large zone emphasis

大きなゾーンを強調する特徴です。

$$
F_{szm.lze} = \frac {1} {N_s} \displaystyle\sum_{j=1}^{N_z} {j^2} s_{.j}
$$

Low gray level zone emphasis

Small Zone Emphasisと似た特徴です。ゾーンが小さいことが強調される代わりに、低いグレーレベルであることが強調されます。

$$
F_{szm.lgze} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} \frac {s_{i.}} {i^2}
$$

High gray level zone emphasis

Large Zone Emphasisと似た特徴です。ゾーンが大きいことが強調される代わりに、高いグレーレベルであることが強調されます。

$$
F_{szm.hgze} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} {i^2} s_{i.}
$$

Small zone low gray level emphasis

この特徴は、ゾーンが小さく、グレーレベルが低いところに位置するGLSZMの左上 1/4 のゾーン数を強調するものです。

$$
F_{szm.szlge} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_z} \frac {s_{ij}} {i^2j^2}
$$

Small zone high gray level emphasis

この特徴はゾーンが小さく、グレーレベルが高いところに位置するGLSZMの左下 1/4 のゾーン数を強調するものです。

$$
F_{szm.szhge} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_z} \frac {i^2s_{ij}} {j^2}
$$

Large zone low gray level emphasis

この特徴はゾーンが大きく、グレーレベルが低いところに位置するGLSZMの右上 1/4 のゾーン数を強調するものです。

$$
F_{szm.lzlge} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_z} \frac {j^2s_{ij}} {i^2}
$$

Large zone high gray level emphasis

この特徴は大きいゾーンで、グレーレベルが高いところに位置するGLSZMの右下 1/4 のゾーン数を強調するものです。

$$
F_{szm.lzhge} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_z} i^2j^2s_{ij}
$$

Gray level non-uniformity

この特徴量は、グレーレベルに対するゾーン数の分布を評価するものです。ゾーンがグレーレベルに沿って均等に分布している場合、特徴値は低くなります。

$$
F_{szm.glnu} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} s_{i.}^2
$$

Normalised gray level non-uniformity

$${F_{szm.glnu}}$$を正規化した特徴です。

$$
F_{szm.glnu.norm} = \frac {1} {N_{s}^2} \displaystyle\sum_{i=1}^{N_g} s_{i.}^2
$$

Zone size non-uniformity

この特徴量は、ゾーンサイズに対するゾーンの分布を評価する特徴量です。ゾーンがゾーンサイズに沿って均等に分布している場合、この特徴の値は低くなります。

$$
F_{szm.zsnu} = \frac {1} {N_{s}} \displaystyle\sum_{j=1}^{N_z} s_{.j}^2
$$

Normalised zone size non-uniformity

$${F_{szm.zsnu}}$$を正規化した特徴です。

$$
F_{szm.zsnu.norm} = \frac {1} {N_{s}^2} \displaystyle\sum_{j=1}^{N_z} s_{.j}^2
$$

Zone percentage

この特徴は、実際に計測されたゾーン数と理論上のゾーンの最大数の割合です。均一性の高いROIは低い値にあります。ゾーン数が多くなるほど、高い値になります。

$$
F_{szm.z.perc}=\frac {N_s} {N_v}
$$

Gray level variance

この特徴は、グレーレベルに対するゾーン数の分散を推定する指標です。

$$
F_{szm.gl.var} = \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_z} (i-\mu)^2p_{ij}
$$

ここで、グレーレベル$${i}$$かつゾーンサイズ $${j}$$をもつゾーンの確率推定値$${p_{ij}}$$と、$${\mu}$$は次のように計算されます。

$$
P_{ij} = s_{ij}/N_s
$$

$$
\mu = \displaystyle\sum_{i=1}^{N_g} \sum_{j=1}^{N_z} i p_{ij}
$$

Zone size variance

この特徴はゾーンサイズに対するゾーン数のばらつきを推定する指標です。

$$
F_{szm.zs.var} = \displaystyle\sum_{i=1}^{N_g} \sum_{j=1}^{N_z} (j-\mu)^2p_{ij}
$$

ここで、グレーレベル$${i}$$かつゾーンサイズ $${j}$$をもつゾーンの確率推定値$${p_{ij}}$$と、$${\mu}$$は次のように計算されます。

$$
P_{ij} = s_{ij}/N_s
$$

$$
\mu = \displaystyle\sum_{i=1}^{N_g} \sum_{j=1}^{N_z} j p_{ij}
$$

Zone size entropy

$$
F_{szm.zs.entro} = -\displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_z} p_{ij} \log_2 p_{ij}
$$

ここで、グレーレベル$${i}$$かつゾーンサイズ $${j}$$をもつゾーンの確率推定値$${p_{ij}}$$は次のように計算されます。

$$
P_{ij} = s_{ij}/N_s
$$

実践

GLSZMの計算

IBSIの上記の例をRadiomicsJで計算して、マトリクスを確認します。

byte pixels[] = new byte[16];
byte r0[] = new byte[] { 1, 2, 2, 3 };
byte r1[] = new byte[] { 1, 2, 3, 3 };
byte r2[] = new byte[] { 4, 2, 4, 1 };
byte r3[] = new byte[] { 4, 1, 2, 3 };
// flatten to create ByteProcessor
int i= 0;
for(byte[] r: new byte[][] {r0,r1,r2,r3}) {
	for(byte v:r) {
		pixels[i++] = v;
	}
}
ImageProcessor bp = new ByteProcessor(4, 4, pixels);
ImagePlus imp = new ImagePlus("sample", bp);
int nBins = 4;// 1 to 4
		
GLSZMFeatures f = null;
try {
	f = new GLSZMFeatures(imp, null ,RadiomicsJ.targetLabel, true /*useBinCount*/, nBins, null);
} catch (Exception e) {
	e.printStackTrace();
}
		
System.out.println(f.toString());

//出力
row[↓]:gray level (1 to N)
col[→]:zone size (1 to N)
==========================
2.0 1.0 0.0 0.0 0.0 
0.0 0.0 0.0 0.0 1.0 
1.0 0.0 1.0 0.0 0.0 
1.0 1.0 0.0 0.0 0.0

特徴量の算出

3D にて、IBSIデジタルファントムで特徴を計算してみます。

ImagePlus ds_pair[] = TestDataLoader.digital_phantom1();
ImagePlus imp = ds_pair[0];
ImagePlus mask = ds_pair[1];
		
RadiomicsJ.targetLabel = 1;
boolean useBinCount = true;
Integer nBins = 6;
Double binWidth = null;
		 
GLSZMFeatures f = null;
try {
	f = new GLSZMFeatures(imp, mask ,RadiomicsJ.targetLabel, useBinCount, nBins, binWidth);
} catch (Exception e) {
	e.printStackTrace();
}
		
System.out.println(GLSZMFeatureType.SmallZoneEmphasis+":"+f.calculate(GLSZMFeatureType.SmallZoneEmphasis.id()));//OK
System.out.println(GLSZMFeatureType.LargeZoneEmphasis+":"+f.calculate(GLSZMFeatureType.LargeZoneEmphasis.id()));//OK
System.out.println(GLSZMFeatureType.LowGrayLevelZoneEmphasis+":"+f.calculate(GLSZMFeatureType.LowGrayLevelZoneEmphasis.id()));//OK
System.out.println(GLSZMFeatureType.HighGrayLevelZoneEmphasis+":"+f.calculate(GLSZMFeatureType.HighGrayLevelZoneEmphasis.id()));//OK
System.out.println(GLSZMFeatureType.SmallZoneLowGrayLevelEmphasis+":"+f.calculate(GLSZMFeatureType.SmallZoneLowGrayLevelEmphasis.id()));//OK
System.out.println(GLSZMFeatureType.SmallZoneHighGrayLevelEmphasis+":"+f.calculate(GLSZMFeatureType.SmallZoneHighGrayLevelEmphasis.id()));//OK
System.out.println(GLSZMFeatureType.LargeZoneLowGrayLevelEmphasis+":"+f.calculate(GLSZMFeatureType.LargeZoneLowGrayLevelEmphasis.id()));//OK
System.out.println(GLSZMFeatureType.LargeZoneHighGrayLevelEmphasis+":"+f.calculate(GLSZMFeatureType.LargeZoneHighGrayLevelEmphasis.id()));//OK
System.out.println(GLSZMFeatureType.GrayLevelNonUniformity+":"+f.calculate(GLSZMFeatureType.GrayLevelNonUniformity.id()));//OK
System.out.println(GLSZMFeatureType.GrayLevelNonUniformityNormalized+":"+f.calculate(GLSZMFeatureType.GrayLevelNonUniformityNormalized.id()));//OK
System.out.println(GLSZMFeatureType.SizeZoneNonUniformity+":"+f.calculate(GLSZMFeatureType.SizeZoneNonUniformity.id()));//OK
System.out.println(GLSZMFeatureType.SizeZoneNonUniformityNormalized+":"+f.calculate(GLSZMFeatureType.SizeZoneNonUniformityNormalized.id()));//OK
System.out.println(GLSZMFeatureType.ZonePercentage+":"+f.calculate(GLSZMFeatureType.ZonePercentage.id()));//OK
System.out.println(GLSZMFeatureType.GrayLevelVariance+":"+f.calculate(GLSZMFeatureType.GrayLevelVariance.id()));//OK
System.out.println(GLSZMFeatureType.ZoneSizeVariance+":"+f.calculate(GLSZMFeatureType.ZoneSizeVariance.id()));//OK
System.out.println(GLSZMFeatureType.ZoneSizeEntropy+":"+f.calculate(GLSZMFeatureType.ZoneSizeEntropy.id()));//OK

//出力
SmallZoneEmphasis:0.25518204081632656
LargeZoneEmphasis:550.0
LowGrayLevelZoneEmphasis:0.25277777777777777
HighGrayLevelZoneEmphasis:15.600000000000001
SmallZoneLowGrayLevelEmphasis:0.025604376417233562
SmallZoneHighGrayLevelEmphasis:2.7633453061224493
LargeZoneLowGrayLevelEmphasis:502.7944444444445
LargeZoneHighGrayLevelEmphasis:1494.6000000000004
GrayLevelNonUniformity:1.4
GrayLevelNonUniformityNormalized:0.28
SizeZoneNonUniformity:1.0
SizeZoneNonUniformityNormalized:0.20000000000000004
ZonePercentage:0.06756756756756757
GrayLevelVariance:2.6399999999999997
ZoneSizeVariance:330.9600000000001
ZoneSizeEntropy:2.3219280948907683

RadiomicsJの引用はこちら

Kobayashi, T. RadiomicsJ: a library to compute radiomic features. Radiol Phys Technol 15, 255–263 (2022). https://doi.org/10.1007/s12194-022-00664-4

RadiomicsJのリンク

https://github.com/tatsunidas/RadiomicsJ

Stay visionary

Radiomics超入門：Gray Level Size Zone Matrix特徴

概要

特徴の集約

近傍を探索する距離

GLSZM特徴

Small zone emphasis

Large zone emphasis

Low gray level zone emphasis

High gray level zone emphasis

Small zone low gray level emphasis

Small zone high gray level emphasis

Large zone low gray level emphasis

Large zone high gray level emphasis

Gray level non-uniformity

Normalised gray level non-uniformity

Zone size non-uniformity

Normalised zone size non-uniformity

Zone percentage

Gray level variance

Zone size variance

Zone size entropy

実践

GLSZMの計算

特徴量の算出

RadiomicsJの引用はこちら

RadiomicsJのリンク

いいなと思ったら応援しよう！