Radiomics超入門：Gray Level Distance Zone Matrix 特徴

2023年9月23日 07:49

概要

Gray Level Distance Zone Matrix（GLDZM）は、グレーレベルごとに計算されたボクセルのグループ（ゾーン）が、ROI エッジ（ROI の端）からどのくらいの距離に存在したかをカウントした行列です [Thibault2014]。GLDZMは、位置とグレーレベルの関係を捉えることに役立ちます。

グレーレベルは、離散化されていることが前提です。

GLDZM を計算するには 2 つのマップが必要です。

1 つ目は、グレーレベルゾーンマップです。これは、GLSZM と同様の方法でゾーンを定義し、どのグレーレベルのゾーンがあるかを調べるためのものです。2 つ目は距離マップです。これについては後で解説します。

ゾーンは、GLSZM と同様に、ある中心ボクセルから見て近傍にあるボクセルが同じグレーレベルのとき、連結していると考えます。ボクセルが近傍に分類されるかどうかは、その連結性（Connectedness）によります。IBSI では、3D アプローチでは 26 connected（26 近傍）、2D アプローチでは 8 connected（8 近傍）で考えます。

ROI エッジまでの距離マップは、3D では 6-connected、2D では 4-connectedに従って定義されます。

同じグレーレベルを持つボクセルグループ（ゾーン）の距離は、ボクセルグループを距離マップに当てはめたときの、ゾーン内の最小距離とします。

距離マップは次のように計算されます。

ROIマスクは適切な（6 connectedまたは4 connectedの）構造要素を用いて形態学的にErodeされる。
Erodeされて削られた全ての ROI ボクセル位置に 1 を加算して距離マップを更新する（距離の最小値は「1」）。
上記のステップを ROI マスクが空になるまで繰り返す。

要は、エッジ位置の距離は「1」、一度Erodeして削られたらその内側は「2」という具合に、Erodeするたびに内側への距離が加算される仕組みです。

GLDZMの結果$${M}$$は、$${N_g \times N_d}$$な行列になります。

ここで、$${N_g}$$はROI 信号強度マスクにあるグレーレベルの数、$${N_d}$$はゾーンの最大距離です。$${M}$$の要素$${d_{ij}=d(i,j)}$$はグレーレベル$${i}$$かつ距離$${j}$$のときのゾーンの数です。

さらに、$${N_v}$$はボクセル数、$${N_s=\sum_{i=1}^{N_g} \sum_{j=1}^{N_d} d_{ij}は全ゾーン数です。

周囲和も同様に定義されます。$${d_{i.}=\sum_{j=1}^{N_d}d_{ij}}$$は、距離に関係なくグレーレベル$${i}$$のゾーンの数です。

同様に、$${d_{.j}=\sum_{i=1}^{N_g}d_{ij}}$$は距離$${j}$$にあるゾーンの数です。

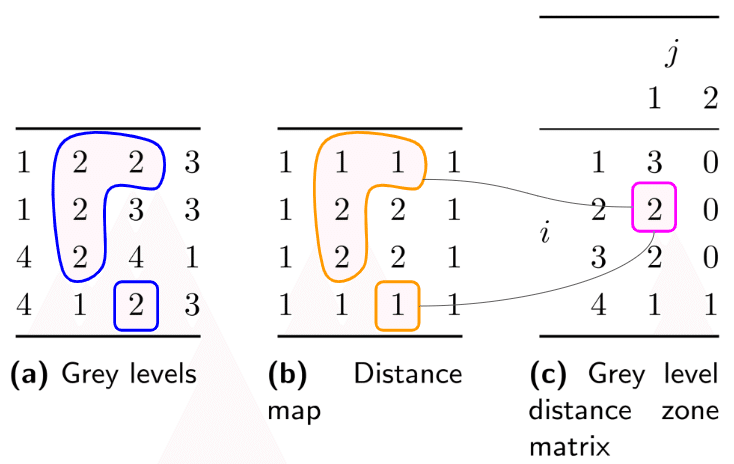
2 次元の例を示します。

GLDZMの例
(a) 元画像
(b) 距離マップ
(c) GLDZM ※4 connectedの場合
Addapted from IBSI ref Fig.17

(a) のグレーレベル「2」に着目した場合、ゾーンが2つあることがわかります（ 2 が 4 つ連なっているゾーンと、2 がひとつだけのゾーン）。ここで、この例では 4 connected を前提に算出している点に注意してください。2 が 4 つ連なっているゾーンは、距離マップに照らし合わせると、ゾーンが含んでいる一番短い距離が「1」、2 がひとつだけのゾーンも、距離は「1」であることから、マトリクスのグレーレベル$${i}$$が 2 で、距離$${j}$$が 1 の要素は「2」カウントとなります。（8 connectedを前提にした場合は、この値は「1」になります。）

マスク

GLDZM はモルフォロジカル ROI と信号強度 ROI の両方の ROI を使用します。距離マップはモルフォロジカル ROI を用いて計算され、信号強度 ROI は GLSZM と同様にゾーンの計算に用いられます。

特徴の集約

GLSZMと同様です。

距離

GLSZMのようにゾーンを計算するため、ゾーンの定義に利用する距離を決定することができますが、大きすぎる距離はゾーンの分割を難しくするため、推奨されません。

GLDZM特徴

GLDZM特徴はGLRLM特徴に基づいて計算されます。

Small distance emphasis

短い距離を強調する特徴です。

$$
F_{dzm.sde} = \frac {1} {N_s} \displaystyle\sum_{j=1}^{N_d} \frac {d_{.j}}{j^2}
$$

Large distance emphasis

長い距離を強調する特徴です。

$$
F_{dzm.lde} = \frac {1} {N_s} \displaystyle\sum_{j=1}^{N_d} {j^2} d_{.j}
$$

Low gray level zone emphasis

Small Distance Emphasisと似た特徴です。距離が短いことが強調される代わりに、低いグレーレベルであることが強調されます。

$$
F_{dzm.lgze} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} \frac {d_{i.}} {i^2}
$$

High gray level zone emphasis

Large Distance Emphasisと似た特徴です。距離が長いことが強調される代わりに、高いグレーレベルであることが強調されます。

$$
F_{dzm.hgze} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} {i^2} d_{i.}
$$

Small distance low grey level emphasis

この特徴は、距離が短く、グレーレベルが低いところに位置するGLDZMの左上 1/4 の距離カウントを強調するものです。

$$
F_{dzm.sdlge} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_d} \frac {d_{ij}} {i^2j^2}
$$

Small distance high grey level emphasis

この特徴は距離が短く、グレーレベルが高いところに位置するGLDZMの左下 1/4 の距離カウントを強調するものです。

$$
F_{dzm.sdhge} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_d} \frac {i^2d_{ij}} {j^2}
$$

Large distance low grey level emphasis

この特徴は距離が長く、グレーレベルが低いところに位置するGLDZMの右上 1/4 の距離カウントを強調するものです。

$$
F_{dzm.ldlge} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_d} \frac {j^2d_{ij}} {i^2}
$$

Large distance high grey level emphasis

この特徴は距離が長く、グレーレベルが高いところに位置するGLDZMの右下 1/4 の距離カウントを強調するものです。

$$
F_{dzm.ldhge} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_d} i^2j^2d_{ij}
$$

Gray level non-uniformity

この特徴量は、グレーレベルに対する距離カウントの分布を評価するものです。距離カウントがグレーレベルに沿って均等に分布している場合、特徴値は低くなります。

$$
F_{dzm.glnu} = \frac {1} {N_s} \displaystyle\sum_{i=1}^{N_g} d_{i.}^2
$$

Normalised gray level non-uniformity

$${F_{dzm.glnu}}$$を正規化した特徴です。

$$
F_{dzm.glnu.norm} = \frac {1} {N_{s}^2} \displaystyle\sum_{i=1}^{N_g} d_{i.}^2
$$

Zone distance non-uniformity

この特徴量は、距離に対するゾーンの分布を評価する特徴量です。ゾーンが距離に沿って均等に分布している場合、この特徴の値は低くなります。

$$
F_{dzm.zdnu} = \frac {1} {N_{s}} \displaystyle\sum_{j=1}^{N_d} d_{.j}^2
$$

Normalised zone distance non-uniformity

$${F_{dzm.zdnu}}$$を正規化した特徴です。

$$
F_{dzm.zdnu.norm} = \frac {1} {N_{s}^2} \displaystyle\sum_{j=1}^{N_d} d_{.j}^2
$$

Zone percentage

この特徴は、実際に計測されたゾーン数と理論上のゾーンの最大数の割合です。均一性の高いROIは低い値になります。

$$
F_{dzm.z.perc}=\frac {N_s} {N_v}
$$

Gray level variance

この特徴は、グレーレベルに対するゾーン数の分散を推定する指標です。

$$
F_{dzm.gl.var} = \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_d} (i-\mu)^2p_{ij}
$$

ここで、グレーレベル$${i}$$かつ距離サイズ $${j}$$をもつゾーンの確率推定値$${p_{ij}}$$と、$${\mu}$$は次のように計算されます。

$$
P_{ij} = d_{ij}/N_s
$$

$$
\mu = \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_d} i p_{ij}
$$

Zone distance variance

この特徴は距離に対するゾーン数のばらつきを推定する指標です。

$$
F_{dzm.zd.var} = \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_d} (j-\mu)^2p_{ij}
$$

ここで、グレーレベル$${i}$$かつ距離サイズ $${j}$$をもつゾーンの確率推定値$${p_{ij}}$$と、$${\mu}$$は次のように計算されます。

$$
P_{ij} = d_{ij}/N_s
$$

$$
\mu = \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_d} j p_{ij}
$$

Zone distance entropy

$$
F_{dzm.zd.entro} = -\displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_d} p_{ij} \log_2 p_{ij}
$$

ここで、グレーレベル$${i}$$かつ距離サイズ $${j}$$をもつゾーンの確率推定値$${p_{ij}}$$は次のように計算されます。

$$
P_{ij} = d_{ij}/N_s
$$

実践

GLDZMの計算

IBSIの上記の例をRadiomicsJで計算して、マトリクスを確認します。

// create 2d array
byte pixels[] = new byte[16];
byte r0[] = new byte[] { 1, 2, 2, 3 };
byte r1[] = new byte[] { 1, 2, 3, 3 };
byte r2[] = new byte[] { 4, 2, 4, 1 };
byte r3[] = new byte[] { 4, 1, 2, 3 };
// flatten to create ByteProcessor
int i= 0;
for(byte[] r: new byte[][] {r0,r1,r2,r3}) {
	for(byte v:r) {
		pixels[i++] = v;
	}
}
ImageProcessor bp = new ByteProcessor(4, 4, pixels);
ImagePlus imp = new ImagePlus("sample", bp);
int nBins = 4;// 1 to 4
		
//init
GLDZMFeatures test =null;
try {
	test = new GLDZMFeatures(
			imp,
			null,
			1,
			true,
			nBins,
			null);
} catch (Exception e) {
	e.printStackTrace();
}
/**
 * In IBSI, their are showing the result of 4-connectedness 2D.
 * But, in reference, "We consider 26-connectedness for a 3D approach and 8-connectedness in the 2D approach."
 * So, RadiomicsJ calculate under 8-connectedness in 2D. 
 */
System.out.println(test.toString(test.getMatrix(true)));

//出力
3.0 0.0 
1.0 0.0 
2.0 0.0 
1.0 1.0

特徴量の算出

3D にて、IBSIデジタルファントムで特徴を計算してみます。

ImagePlus ds_pair[] = TestDataLoader.digital_phantom1();
ImagePlus imp = ds_pair[0];
ImagePlus mask = ds_pair[1];
		
RadiomicsJ.targetLabel = 1;
boolean useBinCount = true;
	
GLDZMFeatures f = new GLDZMFeatures(imp, mask, RadiomicsJ.targetLabel, useBinCount, 6, null);
//マトリクスの確認
System.out.println(f.toString(f.getMatrix(true)));

//features
System.out.println(GLDZMFeatureType.SmallDistanceEmphasis+":"+f.calculate(GLDZMFeatureType.SmallDistanceEmphasis.id()));//OK
System.out.println(GLDZMFeatureType.LargeDistanceEmphasis+":"+f.calculate(GLDZMFeatureType.LargeDistanceEmphasis.id()));//OK
System.out.println(GLDZMFeatureType.LowGrayLevelZoneEmphasis+":"+f.calculate(GLDZMFeatureType.LowGrayLevelZoneEmphasis.id()));//OK
System.out.println(GLDZMFeatureType.HighGrayLevelZoneEmphasis+":"+f.calculate(GLDZMFeatureType.HighGrayLevelZoneEmphasis.id()));//OK
System.out.println(GLDZMFeatureType.SmallDistanceLowGrayLevelEmphasis+":"+f.calculate(GLDZMFeatureType.SmallDistanceLowGrayLevelEmphasis.id()));//OK
System.out.println(GLDZMFeatureType.SmallDistanceHighGrayLevelEmphasis+":"+f.calculate(GLDZMFeatureType.SmallDistanceHighGrayLevelEmphasis.id()));//OK
System.out.println(GLDZMFeatureType.LargeDistanceLowGrayLevelEmphasis+":"+f.calculate(GLDZMFeatureType.LargeDistanceLowGrayLevelEmphasis.id()));//OK
System.out.println(GLDZMFeatureType.LargeDistanceHighGrayLevelEmphasis+":"+f.calculate(GLDZMFeatureType.LargeDistanceHighGrayLevelEmphasis.id()));//OK
System.out.println(GLDZMFeatureType.GrayLevelNonUniformity+":"+f.calculate(GLDZMFeatureType.GrayLevelNonUniformity.id()));//OK
System.out.println(GLDZMFeatureType.GrayLevelNonUniformityNormalized+":"+f.calculate(GLDZMFeatureType.GrayLevelNonUniformityNormalized.id()));//OK
System.out.println(GLDZMFeatureType.ZoneDistanceNonUniformity+":"+f.calculate(GLDZMFeatureType.ZoneDistanceNonUniformity.id()));//OK
System.out.println(GLDZMFeatureType.ZoneDistanceNonUniformityNormalized+":"+f.calculate(GLDZMFeatureType.ZoneDistanceNonUniformityNormalized.id()));//OK
System.out.println(GLDZMFeatureType.ZonePercentage+":"+f.calculate(GLDZMFeatureType.ZonePercentage.id()));//OK
System.out.println(GLDZMFeatureType.GrayLevelVariance+":"+f.calculate(GLDZMFeatureType.GrayLevelVariance.id()));//OK
System.out.println(GLDZMFeatureType.ZoneDistanceVariance+":"+f.calculate(GLDZMFeatureType.ZoneDistanceVariance.id()));//OK
System.out.println(GLDZMFeatureType.ZoneDistanceEntropy+":"+f.calculate(GLDZMFeatureType.ZoneDistanceEntropy.id()));//OK

//出力
1.0 0.0 
0.0 0.0 
1.0 0.0 
2.0 0.0 
0.0 0.0 
1.0 0.0 

SmallDistanceEmphasis:1.0
LargeDistanceEmphasis:1.0
LowGrayLevelZoneEmphasis:0.25277777777777777
HighGrayLevelZoneEmphasis:15.600000000000001
SmallDistanceLowGrayLevelEmphasis:0.25277777777777777
SmallDistanceHighGrayLevelEmphasis:15.600000000000001
LargeDistanceLowGrayLevelEmphasis:0.25277777777777777
LargeDistanceHighGrayLevelEmphasis:15.600000000000001
GrayLevelNonUniformity:1.4
GrayLevelNonUniformityNormalized:0.28
ZoneDistanceNonUniformity:5.0
ZoneDistanceNonUniformityNormalized:1.0
ZonePercentage:0.06756756756756757
GrayLevelVariance:2.6399999999999997
ZoneDistanceVariance:0.0
ZoneDistanceEntropy:1.9219280948874546

RadiomicsJの引用はこちら

Kobayashi, T. RadiomicsJ: a library to compute radiomic features. Radiol Phys Technol 15, 255–263 (2022). https://doi.org/10.1007/s12194-022-00664-4

RadiomicsJのリンク

https://github.com/tatsunidas/RadiomicsJ

Stay visionary

Radiomics超入門：Gray Level Distance Zone Matrix 特徴

概要

マスク

特徴の集約

距離

GLDZM特徴

Small distance emphasis

Large distance emphasis

Low gray level zone emphasis

High gray level zone emphasis

Small distance low grey level emphasis

Small distance high grey level emphasis

Large distance low grey level emphasis

Large distance high grey level emphasis

Gray level non-uniformity

Normalised gray level non-uniformity

Zone distance non-uniformity

Normalised zone distance non-uniformity

Zone percentage

Gray level variance

Zone distance variance

Zone distance entropy

実践

GLDZMの計算

特徴量の算出

RadiomicsJの引用はこちら

RadiomicsJのリンク

いいなと思ったら応援しよう！