
Reinforcement Learning for Variational Quantum Circuits Design
休みが欲しい
休みの日があっても休んでないですね。
絶対勉強の予定は入れてるので。
次の3連休では星が見えるところにでも旅行に行きたいな〜と、まあ日中は旅館かホテルかで勉強してると思いますが(笑)
概要
Reinforcement Learning for Variational Quantum Circuits Design
written by Simone Foderà, Gloria Turati, Riccardo Nembrini, Maurizio Ferrari Dacrema, Paolo Cremonesi
published on Mon, 9 Sep 2024
[Abstract]
Variational Quantum Algorithms have emerged as promising tools for solving optimization problems on quantum computers. These algorithms leverage a parametric quantum circuit called ansatz, where its parameters are adjusted by a classical optimizer with the goal of optimizing a certain cost function. However, a significant challenge lies in designing effective circuits for addressing specific problems. In this study, we leverage the powerful and flexible Reinforcement Learning paradigm to train an agent capable of autonomously generating quantum circuits that can be used as ansatzes in variational algorithms to solve optimization problems. The agent is trained on diverse problem instances, including Maximum Cut, Maximum Clique and Minimum Vertex Cover, built from different graph topologies and sizes. Our analysis of the circuits generated by the agent and the corresponding solutions shows that the proposed method is able to generate effective ansatzes. While our goal is not to propose any new specific ansatz, we observe how the agent has discovered a novel family of ansatzes effective for Maximum Cut problems, which we call $${R_{yz}}$$-connected. We study the characteristics of one of these ansatzes by comparing it against state-of-the-art quantum algorithms across instances of varying graph topologies, sizes, and problem types. Our results indicate that the $${R_{yz}}$$-connected circuit achieves high approximation ratios for Maximum Cut problems, further validating our proposed agent. In conclusion, our study highlights the potential of Reinforcement Learning techniques in assisting researchers to design effective quantum circuits which could have applications in a wide number of tasks.
[Abstract(翻訳)]
変分量子アルゴリズム(VQA)は、量子コンピュータで最適化問題を解決するための有望な手法として登場した。これらのアルゴリズムは、"ansatz"と呼ばれるパラメトリックな量子回路を利用し、そのパラメータがあるコスト関数を最適化する目的で古典的な最適化器によって調整される。しかし、特定の問題に対処するための効果的な回路を設計することが大きな課題である。本研究では、強力で柔軟な強化学習の枠組みを活用し、最適化問題を解く変分アルゴリズムで用いられるansatzとして使用可能な量子回路を自律的に生成できるエージェントを学習する。エージェントは、異なるグラフのトポロジーやサイズに基づく最大カット、最大クリーク、最小頂点被覆などの多様な問題インスタンスで学習される。エージェントによって生成された量子回路と対応する解の分析を行い、提案手法が効果的なansatzを生成できることを示す。我々の目的は特定の新しいansatzを提案することではないが、エージェントが最大カット問題に効果的な新しいansatzファミリーを発見したことを観察しており、これを「$${R_{yz}}$$接続」と呼ぶ。このansatzの特性を、さまざまなグラフトポロジーやサイズ、問題タイプにわたる最先端の量子アルゴリズムと比較して検討する。我々の結果は、$${R_{yz}}$$接続回路が最大カット問題に対して高い近似比を達成することを示しており、更に提案したエージェントの妥当性を確認している。結論として、本研究は強化学習技術が研究者による効果的な量子回路の設計を支援し、幅広いタスクに応用可能である可能性を示唆している。
コンテンツ
強化学習によるansatzの最適化
VQAは、特定の問題に対してansatzを使用し、そのパラメータを古典最適化器で調整して最適解を見つけるアルゴリズムである。
しかし、これそのものに問題があり、対称性など問題固有の特性を利用したり、動的にゲートを追加・削除する適応手法が試みられてきたが、これには多くの計算資源を要する。
強化学習では手動のヒューリスティックや問題固有の知識に頼らずにansatzを生成できる。
また、量子回路設計のような大規模な解空間を持つ問題にも効果が期待できる。
VQA
VQAは、量子コンピュータ上で最適化問題を解くための量子アルゴリズムの1種であり、ansatzと呼ばれる量子回路にパラメータが設定され、古典的な最適化器によってこれらが調整される。
代表的なものにはVQEやQAOA、その派生などがある。
これらのアルゴリズムの問題の1つに、Barren Plateauというものがある。
解空間が大きくなり過ぎてしまい、最適化をする上でパラメータの勾配が0に近くなり、適切なパラメータの探索が困難になってしまう。
この課題に対処するため、適応的に量子回路を構築する方法(ADAPT-VQEやQAOAの適応版)が開発されてきている。
他にも、より一般的な機械学習技術を用いた量子回路の構築、特に強化学習を利用する方法が挙げられる。
強化学習
本研究の目的は、機械学習モデルでハミルトニアンの基底状態を見つけられる量子回路をデザインすることである。
これは量子回路の広範な解空間を探索する必要があり、対象となる特定のハミルトニアンの影響を強く受ける。
そのため、教師あり学習のために量子回路の包括的なデータセットを作成することは現実的ではなく、特定の目標を達成するためにエージェントが環境と相互作用する強化学習のアプローチを選択する。
強化学習は近年、ansatzのパラメータを最適化するのに使われたり、初期状態からターゲットとする量子状態に発展させる量子回路の生成などに使われたりと、量子コンピューティングのタスクにも応用がされている。
しかし、これらの強化学習のエージェントは、主に量子化学の問題を解くものとして設定されていることが多く、他の領域での応用が難しい。
本研究では、新しい強化学習アルゴリズムを導入し、より一般的な最適化問題に適用できるアーキテクチャをデザインする。
エージェント
与えられる最適化問題におけるハミルトニアンの基底状態を探すための量子回路を設計する方法を学習する「RLVQC」という強化学習ベースのアルゴリズムを提案する。
このシステムでのエージェントが操作する環境は、$${n}$$ 量子ビットで構成されたVQCを使用した量子回路で表される。
各エピソードの開始時、量子回路は1層の $${H}$$ ゲートから構成され、エージェントはこの量子回路に新たなゲートを追加する。
環境の状態は、量子回路の構造とそのパラメータに依存する。
エージェントが選択できる行動は、単一量子ビット回転ゲートと2量子ビット回転ゲートの追加をすることである。
単一量子ビット回転ゲート($${R_a^i(\theta)}$$)は、量子ビット $${i}$$ に適用される $${x, y, z}$$ 軸方向の回転を指し、2量子ビット回転ゲート($${R_{ab}^{ij}(\theta)}$$)は異なる2つの量子ビット間でのエンタングルメント生成に使用される。
これらのゲートは、パラメータが0のときに単位行列的な振る舞いをするため、最初のパラメータが0に設定されることで、量子回路の最適化がランダムな初期状態ではなく、有利な状態から始められるという利点がある。
報酬は、エージェントが最適な行動方針を学ぶために必要な情報であり、量子回路の品質に基づいて定義される。
報酬関数は、ハミルトニアンの期待値と量子回路の深さを組み合わせたもので、以下の式で示される。
$${r_t = −\langle H \rangle_t^∗ −\beta \cdot d_t}$$
ここで、 $${\langle H \rangle_t^∗}$$ はハミルトニアンの現在の期待値の推定値、 $${d_t}$$ は回路の深さ、 $${\beta}$$ は量子回路の深さに対するペナルティの重みを調整するハイパーパラメータであり、この報酬設計によってエージェントはハミルトニアンの期待値を最小化しつつ、量子回路の深さも抑えるような行動を学習するよう促される。



本研究で使用する強化学習アルゴリズムはOpenAIのPPOであり、2つのニューラルネットワーク(方策ネットワークと価値関数ネットワーク)を使用してエージェントの行動を決定する。
方策ネットワークは、ある状態に基づいて行動を選択する確率分布を出力し、価値関数ネットワークはその状態の価値を評価する。
これにより、PPOはエージェントが報酬を最大化するための最適な行動方針を学習する。
問題サイズ $${n}$$ に対し、方策および価値関数ネットワークの入力層には $${2^n}$$ 個のニューロンが配置され、環境の状態を表現するベクトルのサイズに対応している。
また、価値関数ネットワークの出力層のサイズは、エージェントが選択できる行動の数に依存する。
エージェントの学習は64エポックで構成され、各エポックは384の行動ステップで構成される。
このステップ数は、複数のプロセスが並行して64ステップずつ行うことで得られる。
各エポックは複数のエピソードからなり、エピソードは初期の $${H}$$ ゲートのみの状態から始まり、以下の終了条件が満たされると終了する。
最大 $${2^n}$$ 回の行動が実行される
報酬が改善されない
報酬が改善されない場合の判断は「Patience」と呼ばれるハイパーパラメータで制御される。
Patienceはエピソード中の行動が最良報酬を更新できなかった場合に減少し、改善が見られた場合には元の値まで増加する。
この仕組みによって、エージェントが無駄な行動を行わないようにする。
学習を通じて、各エピソードで得られた報酬が最大の量子回路を追跡し、学習が終了した後に最良の量子回路を分析する。
エージェントはQUBO形式で定式化された最適化問題を扱う。
対象とする問題は以下の3種類である。
最大カット問題
最大クリーク問題
最小頂点被覆問題
各最適化問題は、異なるグラフトポロジーで実行され、これにより問題の多様性を確保している。
用いられているグラフトポロジーは次の通りである。
3正則グラフ
2Dグリッド
スターグラフ
これらのトポロジーに対して、8頂点および14頂点のグラフサイズで問題が実行され、合計18種類の異なるグラフトポロジーとサイズの組み合わせでRLVQCエージェントを学習する。
本研究のゴールは、エージェントが最適化問題に対して高品質な解をサンプリングするansatzを見つけられるかを評価することにある。
よって、ここでは以下に定義される近似率により評価を行う。
$${\text{A.R.} = \frac{\langle H \rangle^* - \langle H \rangle_{\max}}{\langle H \rangle_{\min} - \langle H \rangle_{\max}}}$$
ここで、 $${\langle H \rangle_{\min}}$$ はハミルトニアンの期待値が取り得る最小値、 $${\langle H \rangle_{\max}}$$ は最大値、 $${\langle H \rangle^*}$$ はRLVQCによって得られた期待値の推定値である。
この近似率は、得られた期待値が最小値に近づくと1に近づき、より高品質な解を意味する。
最大カット問題では $${\langle H \rangle_{\max} = 0}$$ である。
近似率だけでは、最小頂点被覆問題と最大クリーク問題のような制約付き問題で制約を満たしているかどうかを評価できないため、これらに対しては、近似率の閾値が追加されている。
この閾値は、制約を満たす解の中での最小近似率を基準とし、近似率がこの閾値を下回る量子回路は、制約を満たさない可能性が高いことを示す。
なお、最大カット問題ではこの閾値は0として扱われる。
また、エージェントが生成する量子回路の構造も評価項目の1つであり、以下のものが計測される。
単一量子ビットゲートの数
2量子ビットゲートの数
量子回路の深さ
RLVQCによって生成された回路がどの程度効率的で、かつ深さが抑えられているか、ノイズに対する耐性や計算資源の節約につながる要素がこれらによって評価される。
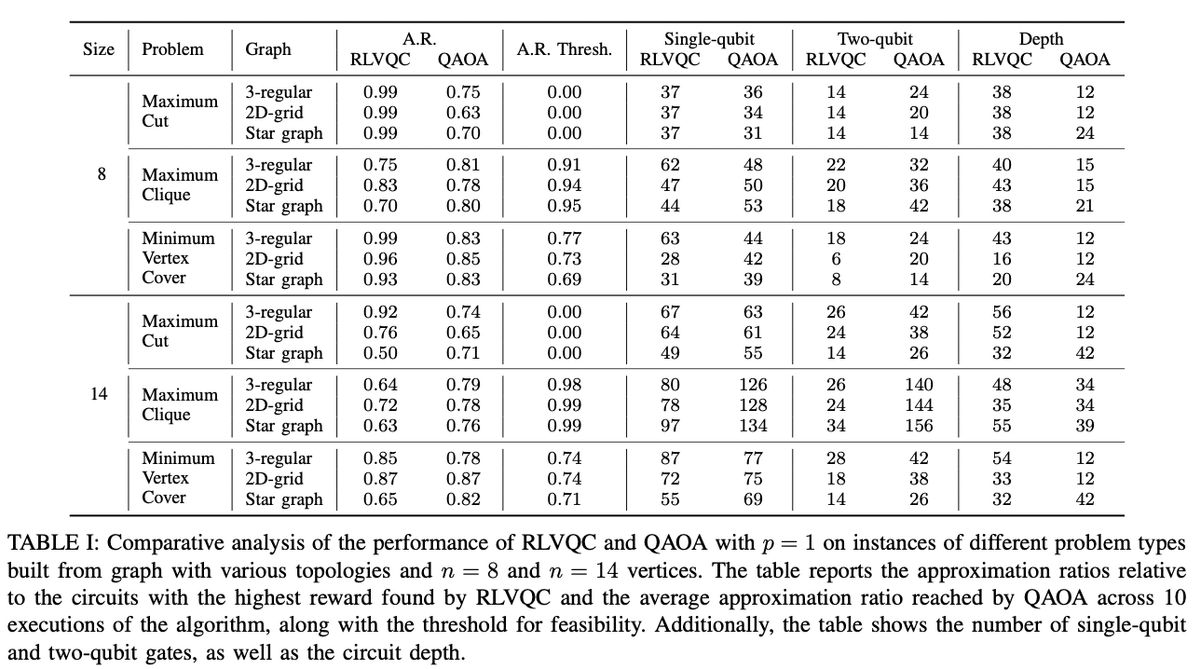
結果
上で定義した評価指標でRLVQCアルゴリズムを実行・評価した。
比較対象として、 $${p = 1}$$ のQAOAで同一条件下で実験を行っている。
RLVQCが得た近似率は、解こうとする問題の種類によって異なる影響を受ける。
最大カット問題と最小頂点被覆問題においてはQAOAを上回る近似率をほぼ達成できたが、最大クリーク問題においてはQAOAの近似率を下回る傾向があり、全体的な性能が安定しないことが示された。
最大カット問題に対して、RLVQCは非常に高い近似率を達成しており、特に8頂点のインスタンスでは、RLVQCは0.99の近似率を記録した。
この問題に対してRLVQCが追加するゲートは $${R_{yz}}$$ 回転に限られており、これにより効率的な量子回路が構築されていることが確認されている。
RLVQCが生成した量子回路とQAOAの量子回路構造を比較すると、RLVQCは一般的にQAOAと同程度のゲート数を使用しながらも、深さはやや高めになっている傾向がある。
RLVQCは深さが深くなる傾向があるものの、報酬関数内の $${\beta}$$ ハイパーパラメータを調整することで量子回路の深さにペナルティを与え、浅い量子回路の方が好まれるように調整することも可能である。
結論として、RLVQCはQAOAと同等、あるいは特定の問題(特に最大カット問題)においてはQAOAを超える性能を示した。
RLVQCがこのような高い近似率を達成しているのは、比較的シンプルなエージェント設計と環境および報酬構造に依存しており、量子計算タスク向けにこれらの要素をさらに最適化することで、さらなる性能向上が期待できる。
RLVQCエージェントが最大カット問題の学習中に発見した「$${R_{yz}}$$ 接続ansatz」は、高い近似率を持つ特徴的な構造を持っており、特定の問題に対して効果的な量子回路を生成するための新しい手法として注目される。
$${R_{yz}}$$ 接続ansatzは初期に $${H}$$ ゲートを適用し、その後に $${n - 1}$$ 個の $${R_{yz}}$$ 回転ゲートを追加していくという構造で形成される。
各 $${R_{yz}}$$ ゲートは「ダブル回転ゲート」として機能し、量子ビット間にエンタングルメントを生成する。
これにより、異なる量子ビットが互いに影響し合う構造となり、回路がより複雑な状態を表現できるようになる。
この構造により、すべてのビットが反転しても解のコストが変わらない対称性を持つ最大カット問題に対して効果的であると考えられる。
この $${R_{yz}}$$ 接続ansatzの中でも「線形量子回路」と呼ばれる構造は注目されており、多様なグラフ構造に対して線形量子回路は非常に高い近似率を達成した。


この理由を理解するために調査したところ、線形量子回路は低コスト解に集中した分布を持つことが確認された。
QAOAは解が分散した広範囲の分布を持ち、探索が広範囲に及ぶため、さまざまな解の候補を提供する点でRLVQCの方が優れていると言える。

$${R_{yz}}$$ 接続ansatzは量子回路の実行において重要なハードウェア要件(量子回路の効率性、精度、量子ビット間の接続性)を考慮した設計となっている。
これは、ハードウェア上で直接実装しやすく、リソースを効率的に使用しながら、ハードウェアの制約に応じた適応が可能である。
結論と展望
本研究では、RLVQCを導入し、最適化問題を解く量子回路設計を学習することができた。
特に最大カット問題においては従来の手法より遥かに優れた結果を残すことができた。
更に、 $${R_{yz}}$$ 接続ansatzを分析し、これが最大カット問題に置いて高い近似性能を有することを示した。
これにより、強化学習アルゴリズムが一般的な最適化問題を解くための量子アルゴリズムの量子回路設計を助ける可能性が現れた。
感想
なんか強引に結論付けてますが、QAOAってそもそも「良いアルゴリズム」じゃないし、扱っている問題の規模を考えると将来性は…。
まあ強化学習アルゴリズムを用いて量子回路設計をするという発想自体は今後の展望にある通り良いと思いますが、この論文を皮切りに指数関数的に発展していくということはまず間違いなく無いでしょうね。
