
リバーにおけるバリューの下限の決定方法
はじめに
みなさんはベットする時に、何を基準にバリューレンジの下限となるハンドを決めていますか?
おそらく、多くの人が”感覚”に基づいて決めていたり、ソルバーの出した答えをそのまま暗記したりしているのではないでしょうか?
人間の感覚には揺らぎがあるため、ポーカーに関する判断を”感覚”に基づいて決定するのは、きわめて危険です。
その日の体調、流れ、感情などに、大きく左右され、いつでもどこでも安定したプレーを継続することが難しくなります。
そこで、本記事では、簡単な単一ストリートのトイゲームについて考察したのちに、”感覚”より一段階上のより論理的なバリューの下限の設定基準について解説する。
その上でGTO wizardを用い、トイゲームで示したバリューの下限の決め方が現実問題に則していることを確認する。
本記事の読み方
本記事では、知りたい人のために数学的な背景についても可能な限り簡明に説明しているが、この記事を読んでくれる方の中には、数式をできるだけ見たくない数学アレルギーの方も一定数いるのではないかと思う。
数式をできるだけ見たくないという方は、「MDFの計算方法→簡易的なバリューの下限の算出方法→トイゲーム(まとめ)→実践編~」の内容だけでも読んでいただければ、この記事の内容は概ね理解できるはずである。
リバーの簡易的なトイゲーム
ゲームの設定
IP、OOPは共に1〜100までのカードを等しい確率で持っている
カードの数字が大きいプレーヤーがポットを獲得することができる
IP、OOPは共に100のスタックを持っており、ポットには100ある
OOPは強制でチェックさせられ、IPはそれに対して、ALLINまたはチェックを選択できる
OOPはMDF(最小ディフェンス頻度)でディフェンスする。
MDFの計算方法
MDFにおいては、OOPはIPのブラフハンドのEVが+にならないようにディフェンスする。(※1)
OOPのディフェンス頻度を f [%]とすると、IPのブラフ成功率は100-f[%]となる。
ブラフが成功した場合に得られる利得は+100、ブラフが失敗した時に得られる利得は-100である。
したがって、IPのブラフハンドのEVは
+100 × (100 - f)/100 + (-100) × f/100 = 100 - 2f
となる。
このEVがプラスにならない頻度で守るので
100 - 2f <= 0
を満たす最小のfを求めれば良い。
式を変形すると
f >=50
とわかり、MDFは50 [%]とわかる。
より一般的には、ポットサイズをp、ベットサイズをbとすると、最小ディフェンス頻度fは
f = p / (p+b)
で算出できる。
上で述べた内容をより一般的な事象に当てはめて考えると上式が導出できるので、興味のある方は自分で導出してみてください。
※1
厳密には、「IPのブラフハンドのブラフEVがチェックEVと同じになるようにディフェンスする」というのが正しいです。
そのため、GTOにおけるIPのディフェンス頻度は厳密には、本記事で算出している頻度と比較して低くなります。
ただし、実践における多くのシチュエーションにおいてはブラフハンドのチェックEVが0である場合が多いため、ブラフハンドのチェックEVが0であるこちらのMDFのほうが現実問題に則していると言えます。
ハーフストリートの[0,1]ゲームの厳密な均衡解については、glassさんの記事で説明されているので、興味のある方はそちらの記事を参考にしてください。
IPの各ハンドのチェックEVを求める
まず、前提としてこのゲームにおけるカードの数字は相手レンジに対するそのハンドのおおよそのEQに対応する。
カードの数字が80であれば、1-79までの79%のハンドに勝っており、80に対してのチョップであり、81-100までの20%のハンドに負けている。
80の持つEQは、79 × 1 + 0.5 + 20 × 0 = 79.5[%]
である。
IPが持っているハンドの数字を x とすると、そのハンドはx - 0.5 [%]の確率でポットを獲得できる。
ポットのサイズが100であるため、チェックした際のそのハンドのEVは
100 × (x - 0.5)/100 = x - 0.5
である。
IPの各ハンドのベットEVを求める
ベットした場合のEVを計算するためには、
①ベットにコールされた場合
③ベットにコールされない場合
の2つのパターンの利得をまとめればよい。
①ベットにコールされた場合
OOPはMDF通りにディフェンスするので、コールされる確率は50[%]である。
したがって、IPのカードの数字がxの場合、xの相手のコールレンジに対する勝率は ( ( x-0.5-50 ) / 50 ) ×100 = 2x - 101 [%]である。
また、コールされてポットを獲得した場合の利得は+200である。
コールされて負けている確率は
100 - (( x - 50 - 0.5 ) / 50) × 100 = 100 - ( 2x -101 ) = 201 - 2x [%]
コールされて負けた場合の利得は -100である。
したがって、この事象のEVは
( 2x - 101 )/100 × 200 + (201 - 2x)/100 × (-100)
= 4x - 202 - 201 + 2x
= 6x - 403
である。
②ベットにコールされない場合
この場合はIPが100のポットをすべて獲得する。
よってIPの利得は +100である。
①②からIPのベットEVは
1/2 × (6x-403) + 1/2 × 100 = 3x - 201.5 + 50 = 3x -151.5
と求まる。
ベットがチェックより利益的になる条件とは?
IPの持つハンドのEQがx [%]の時、チェックEVとベットEVはそれぞれ
チェックEV = x - 0.5
ベットEV = 3x -151.5
と求まった。
ベットがチェックより利益的になる条件というのは、単純にベットEVがチェックEVを上回ることである。
したがって、
3x -151.5 >= x - 0.5
を満たすxは、ベットが利益的になる。
この方程式を解くと、
x >= 75.5
と求まる。
したがって、IPは76以上のカードを持っている場合に、ベットしたほうが得であるとわかる。
簡易的なバリューの下限の算出方法
上記で、触れてきたEVの計算は実践的に用いるのには難しいと感じるのが普通である。そこでより簡単な、バリューの下限の算出方法について説明する。
ここからは式の意味を理解する必要は特になく、暗記してもらえればよい。
早速本題の簡略化した式を以下に示す。
EQ閾値 = 100 - (f/2)
f : (MDFに基づいて算出された)OOPのディフェンス頻度 [%]
で求められる。
MDFの計算については、上の導出の中で計算したものを、参考にしていただきたい。
今回扱った、簡易的なトイゲームにおいては、MDFが50 [%]であったため、バリューベットの下限は、100 - ( 50 / 2 ) ≒ 75である。(※2)
※今回扱ったトイゲームはカードの値として離散値を用いてしまったため、簡易式で求めたバリューの下限と厳密に求めたバリューの下限が異なっています。基本的には、簡易的なもので正しいです。
トイゲーム(まとめ)
MDF(最小ディフェンス頻度)はベットする側のブラフハンドのEVがゼロになるようなディフェンス頻度のことである。
ポットサイズをp、ベットサイズをbとすると、最小ディフェンス頻度fは
f = p / (p+b)
で算出できる。
OOPがf[%]の頻度でディフェンスする場合においては、IPのバリューの下限は、
EQ閾値 = 100 - (f/2)
で求められる。
実践編
ここでは、リバーで異なるサイズのALLIN or Checkとなるような二つの場合において、先ほどトイゲームで求めた論理的なバリューの下限が一致しているか確認する。
①BTN vs BB SRP eff 50bb
◎Flop KhTc3d(5.5bb)
BB(47.5bb) x / c
BTN(47.5bb) bet 1.8bb
◎Turn 6d(9.1bb)
BB(45.7bb) x / c
BTN(45.7bb) bet 11.4bb
◎River 2h(31.9bb)
BB(34.3bb) x
BTN(34.3bb) ?????
フロップターンの全ての要因は、GTO wizard 50NL general solution eff 50bbのソリューションに基づいている。
バリューの下限となるEQの閾値を計算する
今回はポットが31.9bb、リバーのベットサイズが34.3bbなので、OOPのMDFは、
34.3 / (31.9 + 34.3) = 0.481… ≒ 48[%]
したがって、バリューハンドのEQの下限は
EQ = 100 - (48/2) = 76%
と計算できる。
最適戦略
次に実際の最適戦略を確認する。
GTO Wizardのブレークダウン機能からIPの戦略の詳細を確認すると、トップペア+のハンドでバリューALLINをしているとわかる。
ハンド毎の戦略を確認すると、IPのバリューの下限はKJであるということが確認できる。


次に、KJのEQがどのぐらいあるのかについて確認する。
KJの戦略について詳細に表示すると、EQが78%あるKJはバリューALLINを選択し、EQが77%に満たないKJはチェックするということが分かる。
どうやら、77%~78%の間にバリューの閾値があるようだ。

先ほど、論理的に算出したバリューの下限のEQは、76%であった。
論理的なバリューの下限と、現実のSolutionがおよそ一致していることが確認できた。
では、一体"なぜ"論理的に求めたバリューの下限と、最適戦略が指し示すバリューの下限が異なるのだろうか?
トイゲームの結論と実際のバリューの下限が異なる理由
この理由は端的に言えば、お互いの持つレンジの性質が異なるからである。
トイゲームにおいては、仮定として「お互いが完全に同一の1~100までのカードを持つ」という、レンジに対する制約を課していた。しかし、このスポットでは、ナッツ級のハンドが一方的にBTN側に存在している。
そのため、ALLINに対して、BB側はMDF通りにディフェンスできない。
以下にALLINを受けた場合のBB側の最適戦略を示す。
BB側はKのワンペアを中心に、レンジの上位45.4%をディフェンスしている。
先ほど、計算したMDFは48%であったから、このスポットにおいてはBB側はMDFと比較して2.6%多くフォールドしていることが分かる。
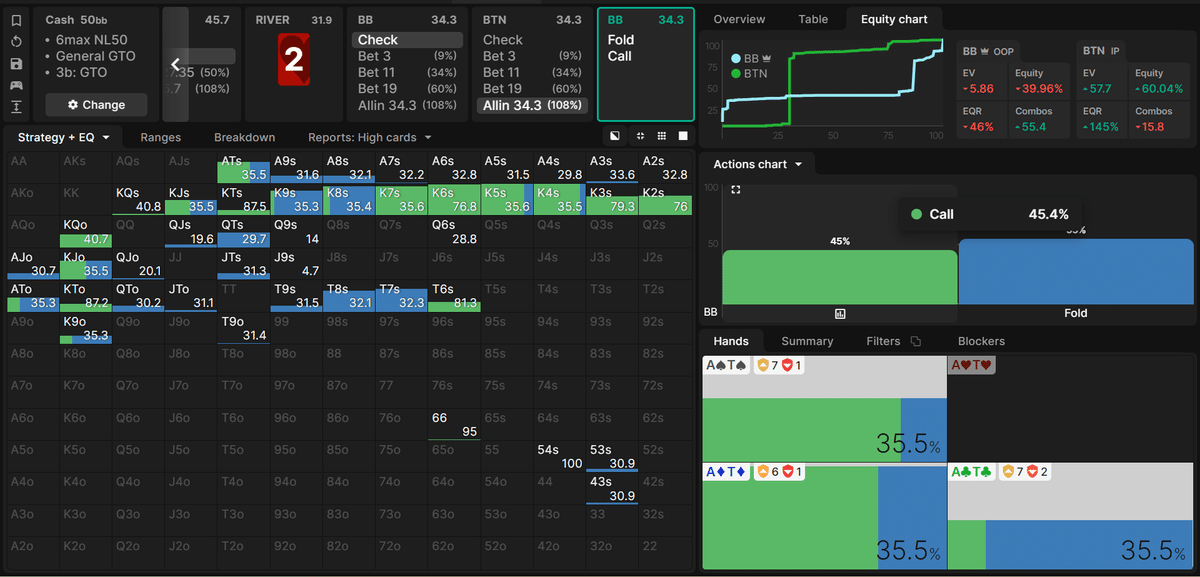
BB側がレンジの上位45.4%をディフェンスする場合、バリューの下限の算出式から、
EQ = 100 - (45.4/2) = 77.3 [%]
と計算できる。
ここで、実際の最適戦略にもう一度立ち返ると、最適戦略ではバリューの下限が77~78%の間にあった。
ここから、BBのディフェンス頻度に基づいたバリューの下限と、最適戦略が指し示すバリューの下限が一致することが分かった。
トイゲームに基づいたバリューの下限と、最適戦略におけるバリューの下限が異なる理由は、BBのディフェンス頻度がMDFと比較して低くなるからである。


②BTN vs BB SRP SRP eff 75bb
◎Flop AsTh7d(5.5bb)
BB(72.5bb) x / c
BTN(72.5bb) bet 4.1bb
◎Turn Qs(13.7bb)
BB(68.4bb) x / c
BTN(68.4bb) bet 10.3bb
◎River 2h(34.3bb)
BB(58.1bb) x
BTN(58.1bb) ALLIN 169% or Check
フロップターンの全ての要因は、GTO wizard 50NL general solution eff 75bbのソリューションに基づいている。
バリューの下限となるEQの閾値を計算する
今回はポットが34.3bb、リバーのベットサイズが58.1bbなので、OOPのMDFは、
34.3 / (34.3 + 58.1) = 0.371… ≒ 37[%]
したがって、バリューハンドのEQの下限は
EQ = 100 - (37/2) = 81.5 [%]
と計算できる。
最適戦略
次に実際にWizardで最適戦略を確認する。
IPはツーペア+のハンドでバリューALLINし、7hit、low pocket、Kハイ、Jハイなどのハンドでブラフしていることが分かる。


次にバリューの下限となるハンドのEQについて確認すると、バリューの下限であるA7のEQは最も低いもので83.8%である。

A7の次に強いT7のEQは、75%であり、バリューの閾値を満たしていない。

この例においては、最適戦略が論理的に求めたバリューの下限に従って構築されていることが確認できた。
まとめ
本記事では、簡易的なトイゲームを基に、バリューの下限の論理的な算出方法についてまとめた。
理論に基づいた結果が最適戦略においても反映されているかどうかを検証した。
理論に基づいた計算結果と、最適戦略におけるバリューの下限が異なる場合については、その理由についてBB側の最適戦略を基に考察した。
終わりに
最後まで読んでくれてありがとうございます。
GTO wizardがこれだけ普及している現状においても、GTO(ゲーム理論的最適)が、どのような論理に基づいて計算されているのかについて知らない人が多いと感じます。
本記事がそのような方のGTOへの理解の手助けとなればうれしいです。
本記事が良ければ、スキ、Twitterのフォロー、拡散をお願いします!
引用RT等での感想もお待ちしております!
記事の内容に関して、間違い・誤植等ございましたら、引用RT or DMにてご指摘ください。
P.S.
今回はリバーでOOPからのレイズが発生しない場合の戦略をまとめましたが、現実問題としてはリバーOOPからレイズが返ってくる状態のことが多いと思います。リバーでOOPからレイズが返ってくる条件における戦略についても、数学的な計算は可能ですが、1本の記事ですべてまとめるのは難しいと感じたため、本記事で扱うのはやめました。
また、リバーのALLIN or Checkの戦略が不服に感じる方もいるかもしれません。リバーでレイズが帰ってこないノードロック下における複数サイズを用いた最適戦略についても、需要がありそうならばまとめます。
