微分：データサイエンティストへの道（１６）

１：微分
　　まず、微分の勉強です。
　　それは下記の画像になります。

２：常微分、偏微分ともにsp.diff()を使用します。
　※sp.Derivative()では、与式表示します。
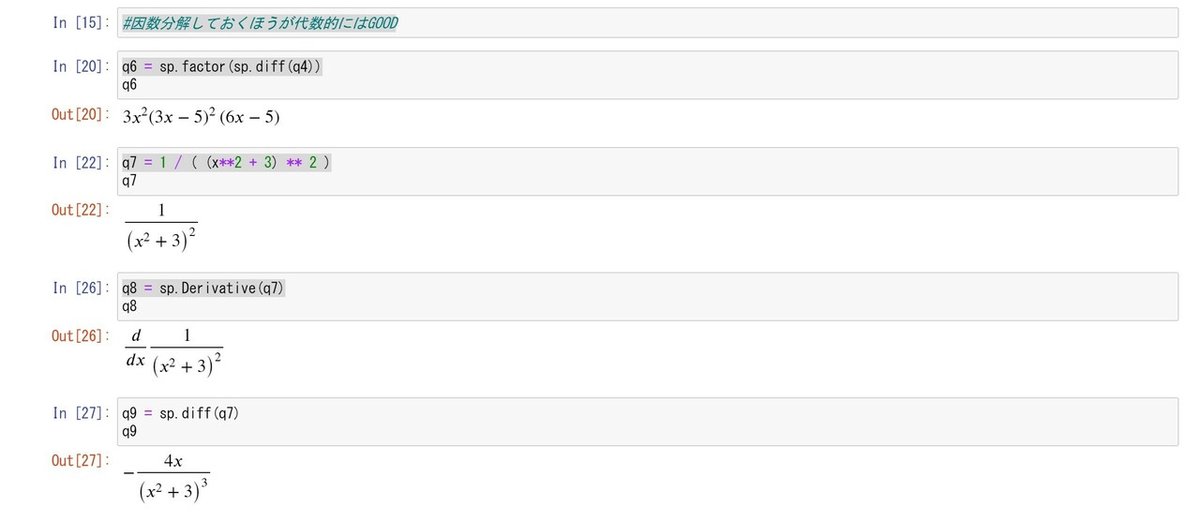
　※解答は代数的には因数分解しておくほうがよいです。

[微分]
X³-2X²+5　の場合
　q1 = x**3 - 2*x**2 + 5
   sp.Derivative(q1)
   sp.diff(q1)

[微分]
e✖　（ネイピア数をxで微分）する場合
　q2 = sp.E**x
　sp.Derivative(q2)
　sp.diff(q2)

[微分]
log  x
     e　　の場合

　q3 = sp.log(x , sp.E)
　sp.Derivative(q3)
　sp.diff(q3)

[微分]
(3x²-5x)³　の場合
　q4 = (3*x**2 - 5*x) ** 3
　q5 = sp.Derivative(q4)
#因数分解しておくほうが代数的にはGOOD
　q6 = sp.factor(sp.diff(q4))

[微分]
1 / (x²+3)²　の場合
　q7 = 1 / ( (x**2 + 3) ** 2 )
    q8 = sp.Derivative(q7)
    q9 = sp.diff(q7)

[偏微分]
∂ 
-  (2x²+3xy-5y³)　
∂x  　　　　　　　　の場合
　q1 = 2*x**2 + 3*x*y - 5*y**3
　q2 = sp.Derivative(q1 , x)
　q3 = sp.diff(q1 , x )

∂ 
-  (2x²+3xy-5y³)　
∂y  　　　　　　　　の場合
　q4 = sp.Derivative(q1 , y)
　q5 = sp.diff(q1 , y)

∂ 
-  (√x³+√cos(xy))　
∂y  　　　　　　　　の場合
　q6 = sp.sqrt( x**3 + sp.cos(x*y) )
　q7 = sp.Derivative(q6 , x)
　q8 = sp.factor(sp.diff(q6 , x))