AtCoder ARC156 B - Mex on Blackboard

2023年3月2日 13:10

考えたこと

・数値の種類数が増えなければ重複組み合わせ

入力例1を見ると、1回目の操作では0, 1, 2の3種類の数値を書き込むことができる。
(入力例1はK = 1だが)仮に2回目の操作を行った場合、1回目の操作で2を書き込んでいたら2回目に選択できる数値の種類数が増えてしまう。
もしこの問題に、「存在しない数値は書き込めない」という制限があったらどうだろうか。選択できる数値の種類数が増えることはなく、入力が"0, 1, 3"なら延々と0か1を書き込むだけになる。
この場合、「0→1の順で書き込む」のと「1→0の順で書き込む」のは同じ意味である。この問題は最終的に何がいくつ書かれているかにしか興味はなく、操作の順番は問題の答えに影響しないからである。
そのため組み合わせの数は重複組み合わせで導出することができ、
　　(n+r-1)Cr
　　　　n：選ぶことができる数値の種類数
　　　　r：何回選ぶか
で求められる。

・各操作ごとに、存在しない数値の中で最小のものを1つ生み出すことができる

入力例1を見ると、1回目の操作では新規で2を書き込むことができる。
仮に1回目の操作で選択する数値に3を含めたとしても、3より小さい2がまだ存在していないため4以上の数値を新規で書き込むことはできない。
1回目に2を書き込めば、2回目には0～3の全てを選択することで4を書き込むことができる。
すなわち新規開拓は、その時に存在しない数値の中で最小のものしか開拓することができないと言える。

・新規開拓も順不同である

入力例1をK = 3に変更して考える。例えば答えの一つに(0, 1, 1, 2, 2, 3)という集合を作ることができるが、これの作り方は
　　①1を書き込む→2を新規開拓→2を書き込む
　　②2を新規開拓→1を書き込む→2を書き込む
　　③2を新規開拓→2を書き込む→1を書き込む
の3パターンがある。しかし最終的に書かれているものは同じなので、どの方法で作ってカウントしても(重複カウントしなければ)問題ない。
先に述べた通り、新規開拓しなければ重複組み合わせで求められるので、②と③は区別する必要がなく公式で瞬時に求めることができる。
そのため、選択できる種類数が増えてしまう新規開拓を先に行うように固定すれば求めやすくなる。
さらに新規開拓できる数値は、現在存在しないものの中で最小のものに限られるので、新規開拓する回数を決めれば重複組み合わせで選択できる種類数も自ずと決まる。
つまり、新規開拓する回数でループを回してその時の組み合わせ数を求めて、その和を取ればいい。

・エクセルで試してみる

入力例3で試してみる。

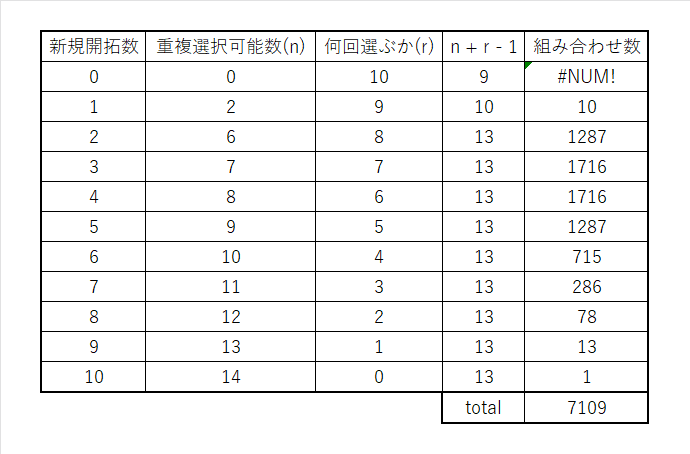
　・新規開拓0個の場合
　　　入力に0がないため、新規開拓0個は不可能である。
　・新規開拓1個の場合
　　　0を新規開拓し、0, 1の2種類から9回選ぶことになる
　・新規開拓2個の場合
　　　0, 2を新規開拓し、0～5の6種類から8回選ぶことになる
　・新規開拓2個の場合
　　　0, 2, 6を新規開拓し、0～6の7種類から7回選ぶことになる
　(以下略)

これをうまい具合にコードに起こせばいい。mod○○の世界で組み合わせ数を求める関数などは検索すれば出てくるし、それがなくてもmod○○の世界で割り算を行う関数があれば実装は可能である。

書いたコードと提出結果

#include <bits/stdc++.h>

int mod = 998244353;

long long modinv(long long dividend, long long divisor, long long modnum){
    long long b = mod, u = 1, v = 0;
    while (b) {
        long long t = divisor / b;
        divisor -= t * b; std::swap(divisor, b);
        u -= t * v; std::swap(u, v);
    }
    u %= mod; 
    if (u < 0) u += mod;
    long long ans = dividend * u % mod;
    return ans;
}

int main(){
    int N, K;
    std::cin >> N >> K;
    std::vector< int > A(N);
    std::vector< bool > exist(2*N+1, false);
    for(int i=0; i<N; i++){
        std::cin >> A[i];
        exist[A[i]] = true;
    }
    
    long long cu = 1, cd1 = 1, cd2 = -1;
    int cu_cnt = 0, cd1_cnt = 0, cd2_cnt = -2;
    for(int i=0; i<K-1; i++){
        cu_cnt++;
        cu = (cu * cu_cnt) % mod;
    }
    for(int i=0; i<=K; i++){
        cd1_cnt++;
        cd1 = (cd1 * cd1_cnt) % mod;
    }
    
    long long ans = 0;
    int index = 0;
    for(int i=0; i<=K; i++){
        while(exist[index]){
            index++;
            
            cu_cnt++;
            cu = (cu * cu_cnt) % mod;
            cd2_cnt++;
            if(cd2_cnt == 0){
                cd2 = 1;
            }else{
                cd2 = (cd2 * cd2_cnt) % mod;
            }
        }
        index++;
        
        cd1 = modinv(cd1, cd1_cnt, mod);
        cd1_cnt--;
        cd2_cnt++;
        if(cd2_cnt == 0){
            cd2 = 1;
        }else{
            cd2 = (cd2 * cd2_cnt) % mod;
        }
        
        if(cd2_cnt < 0){
            continue;
        }
        long long ans_tmp = modinv(cu, (cd1 * cd2) % mod, mod);
        ans = (ans + ans_tmp) % mod;
    }
    
    
    std::cout << ans << std::endl;
    
    return 0;
}

終わりに

あまり学校では詳細にやっていなかったかもしれないが、重複組み合わせ数の求め方はAtCoderでは頻出である。
公式丸暗記の必要はないが、公式が存在することは覚えておくべきだと思う。