AtCoder ABC292 F - Regular Triangle Inside a Rectangle
考えたこと
・長方形の1頂点を正三角形の1頂点にしたほうがいい
なるべく正三角形の辺を大きくしたいので、長方形の端までしっかり利用したほうがいいのは直感的に正しそうである。
図にすると以下のような感じ。

なので、以降は長方形の1頂点を正三角形の1頂点に採用するケースのみを考える。
・角度を決めれば、作れる最大の正三角形も決まる
長方形の1頂点を正三角形の1頂点に採用すると決めているため、長方形と共有している1頂点についてどのような角度で正三角形を配置するかによって作れる最大の正三角形の大きさも決まる。
図にすると以下のような感じ。
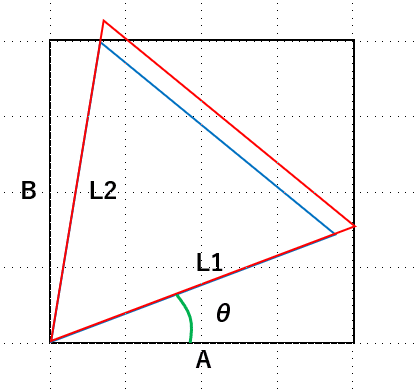
図の緑部分の角度を決めれば、その角度で長方形にぶつかるところまで辺を伸ばしてできる正三角形が最大の大きさである。
長方形と共有している1頂点からは2つの辺が出ているので、両方とも長方形にぶつかるまで伸ばして、小さい方が実際に作ることができる最大の正三角形となる。(大きい方を選ぶと逆側の辺がはみ出る)
ここで図のように長方形と共有している1頂点から出ている2辺の最大の長さをL1, L2とし、長方形の辺AとL1とのなす角をθをすると、L1, L2の長さは
L1 = A ÷ cosθ
L2 = B ÷ sin(θ + 60°)
となる。
長方形の中に正三角形を納めなければならないため、θの定義域は0° ≦ θ ≦ 30°となる。この範囲でmin(L1, L2)が最大となるような角度を探せばいい。
・正三角形の1辺の長さは、θに対して上に凸or単調増加or単調減少
θを変動させると辺の長さがどのように変動するかを確かめるために、まずはエクセルで実装してみた。
実装は図のような感じ。

このAとBを変動させると、グラフはθに対して上に凸, 単調増加, 単調減少の3通りとなった。
極大値が複数現れないのであれば、三分探索で探すことができるので三分探索での実装を考える。
・三分探索とは
極値を複数持たない関数に対して、極値を探索するアルゴリズムである。
具体的には以下のとおりである。(極大値を求める場合)
(1) 探索範囲を決める
二分探索と同様に探索範囲を決める。
ここでは探索範囲の最小値をleft, 最大値をrightと
表現することにする。
(2) left~right間で2点決める
left~right間を3分割して1/3地点と2/3地点の2点を
計測点として決める。
ここでは1/3地点をc1, 2/3地点をc2と呼ぶことにする。
位置関係としては、left < c1 < c2 < rightである。
(3) f(c1)とf(c2)を求める
(4) left, rightの更新
f(c1) > f(c2)だった場合c2~rightの範囲に極大値はないため、
rightにc2を代入する。
f(c1) < f(c2)だった場合left~c1の範囲に極大値はないため、
leftにc1を代入する。
(5) (2)に戻る
十分な回数繰り返したら終了する。
今回は0° ≦ θ ≦ 30°の範囲で極大値を探索するため、left = 0°, right = 30°として三分探索を行えばいい。
・補足 AとBの大きさに差があるとき
AとBの大きさに差がありどちらかがもう一方より数倍も大きかったりすると、
L1 = A ÷ cosθ
L2 = B ÷ sin(θ + 60°)
で求めたときに、L1かL2のどちらかが長方形にぶつかる以上に長くなってしまう。
図にすると以下のような感じ。

求めるべきものは左の図だが、この計算方法だと右の図が求まってしまう。
しかしこのような状況になった場合、計算が不正確になるのはL1, L2のうち大きい方の辺である。
実際に作れる最大の正三角形の辺の長さは、min(L1, L2)で求めるため、不正確側は必ず無視される。
そのため、長方形にぶつかるまでという意図からは違う計算結果になることもあるが、このまま実装しても問題ない。
書いたコードと提出結果
#include <bits/stdc++.h>
int main(){
int A, B;
std::cin >> A >> B;
double ans = 0;
double left = 0.0, right = 2.0 * M_PI / 12.0; // left = 0°、right = 30°
for(int i=0; i<1000; i++){
double c1 = left + (right - left) / 3; // 1/3地点
double c2 = left + (right - left) * 2 / 3; // 2/3地点
double c1_l1 = A / std::cos(c1);
double c1_l2 = B / std::sin(c1 + 2.0 * M_PI / 6.0);
double c1_l = std::min(c1_l1, c1_l2);
double c2_l1 = A / std::cos(c2);
double c2_l2 = B / std::sin(c2 + 2.0 * M_PI / 6.0);
double c2_l = std::min(c2_l1, c2_l2);
if(c1_l > c2_l){
right = c2;
ans = c1_l;
}else{
left = c1;
ans = c2_l;
}
}
std::cout << std::setprecision(20) << ans << std::endl;
return 0;
}
終わりに
解説に二分探索って書いてあるけど、二分探索でどうやるの?
