100の2乗までの平方数を覚える方法

うつろです。

突然ですがみなさん、数学は好きですか？
少なくともこのタイトルを見て開いてる時点で、多少は興味がおありなはずです。

さて今回は、1の2乗から100の2乗までをパッと計算する方法を伝授します。インドなんかでは2桁×2桁の掛け算は全部暗記するらしいですが、そんなことしている暇はないのでいろんな技を駆使して計算をラクにしていきます。

そもそもなんでそんなことするんですか

純真無垢な誰かからこんな声が聞こえてきた気がするのであえて言いましょう。

趣味です。

ぶっちゃけ覚えてなかろうが、人生そこまで損することはありません。「こんなことやってるくらいならゲームしてた方が楽しいよ！」と言われると、実際そうかもしれない。

でも覚えてみると、意外と面白いものです。
「9409」という数字を見たときに、「あ！97の2乗じゃん！」って言える人生も、なかなかどうして楽しいですよ。

まあ覚えなくてもいいので、とりあえず最後まで見てってください。

どこまで暗記してますか？

ちなみに、平方数どこまで暗記してますか？
九九を覚えていたら、10の2乗まではいけますね。ある程度興味がある方なら、20の2乗くらいまでは暗記してるんじゃないでしょうか。

実は100までの平方数を覚えるとなると、これでは足りません。
40の2乗まではがんばりましょう。しんどいけど。

ある意味いちばんの難所かもしれません。語呂合わせとかもないですが、あえて言うなら

・22、33、44の平方数は11の倍数なので、奇数桁の総和と偶数桁の総和を引いたものが11の倍数になる (この3つに関しては0になる)


・32は2の5乗だから、32の平方数は2の10乗、つまり1024。同様に27は3の3乗だから、27の平方数は3の6乗、つまり729


・37〜39までの平方数の下3桁は
369 (3の倍数) → 444 (ゾロ目) → 521 (ゴツい)
と、まずまずの覚えやすさ

まあこんなもんでしょうか。
語呂合わせ、1個使っちゃいましたね。

ここまで覚えたらついにテクニックの出番です。まずは41〜60の平方数。

上2桁と下2桁で分けて考える

41〜60までは、王道の覚え方があります。
それは上2桁と下2桁に分けること。

こちらをご覧ください。

41〜45までの平方数

上2桁は+1、下2桁は1〜9までの平方数というふうに決まってるんですね！
これが60の平方数まで続きます。

この法則についてはこちらの計算式で種明かしができます。

50と比べてどれくらい離れているかによってxの値が決まり、これを代入することでローラー式にそれぞれの平方数が求められていくという寸法です。
初めは慣れませんが、覚えてくると案外すんなり出すことができるようになってきます。

11〜40の平方数を駆使する

61〜90の平方数は一番の鬼門です。ここで上の章で覚えた、11から40までの平方数が役に立ってきます。

やり方は至ってシンプル。先ほどのこの式

のxに、11〜40までの平方数を代入していけばいいわけです。
だんだん繰り上がりが増えてきてまどろっこしくなってきますが、足し算なのでそこまで苦にはならないはず。紙を使わずできるようになったらそれだけで儲けものです。

最後は100からの引き算でラクに

91〜100までの平方数は、100からどれだけ離れているかを計算することで簡単に計算ができます。

40〜60の平方数とやり方は同じです。こちらの計算式を利用してやってみてください。頭に2がつくので、xが1増えるごとに上2桁の数字が2ずつ増えていくのは注意ポイントですね。

下1桁が1 or 5 or 9なら、もっとラクに計算できる

下一桁を固定して、10の位の数をnとおくと、面白い法則が見えてきます。
まずは下一桁が5のとき。(これは有名かもしれません)

なんともきれいな形になります。100n(n+1)は確実に100の倍数なので、下2桁は必ず25となり、上2桁についてもn(n+1)を計算するだけでわかりますから超簡単です。

また、下1桁が1 or 9の場合でも、これには劣りますがきれいな形にできます。

±を使って1つにまとめてみました。n(5n±1)の計算、少し面倒かもですが他の数字が下一桁に来たときよりはよっぽどマシです。

ちなみにこれらは100以上の数字についても同様に使えるので便利です。

すべてを解決する「超インド式計算」とは？

ちなみにもっと応用したもので「超インド式計算」というのがあります。これは2桁の数字をそれぞれ

に当てはめて計算するというやり方で、高1で習う分配法則の応用になります。

例えば37×76を計算するなら、

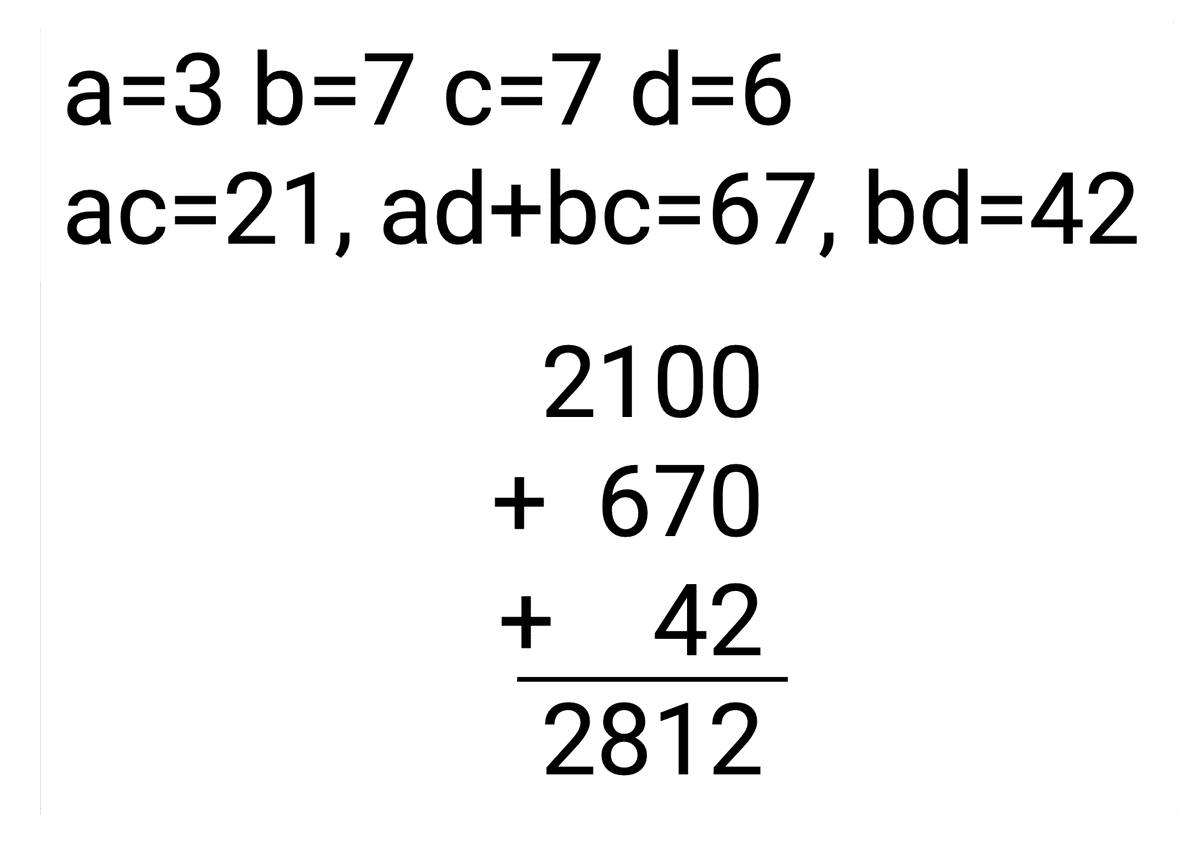
のようになり、答えが2,812とわかる、という感じです。こんなふうに平方数に限らず、どんな2桁×2桁の計算もできてしまうのが、この計算方法の魅力です。

頭の中で筆算するよりも計算ミスが少なくなりますが、過程が多いので若干難しいです。できるに越したことはないですが人を選ぶとの理由から今回は除外しました。

いかがでしたか？
最後は練習あるのみ。何度も反復練習して、平方数だけでも完璧になりましょう！

また読んでね。