k-means法のはなし

Introduction

このノートは、多変量解析やデータマイニングを知りたい人向けにクラスタリングについて紹介するシリーズの2記事目（1記事目はこちら）になります。今回は分割最適型クラスタリングとして知られるk-means法について紹介します。

1.  k-means法の概要

k-means法はクラスター数Kを事前に決めておき、データポイント全体をK個のクラスターに分割する手法の一つです。特にクラスターは

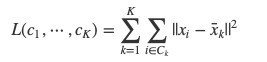
が最小になるようなクラスターC[1],...,C[K]を決定します。なお、各クラスターの重心のことをセントロイドと言います。この最適化問題は一般にNP困難であるため、一般には以下のようなヒューリスティクスによる最適化アルゴリズムが用いられます。

1. ランダムに各データポイントをクラスターに割り振る。
2. 以下の操作を繰り返す。
(a) 各クラスターの重心（平均値）を求め、各データポイントからの距離を求める。
(b) 各データポイントを最も近い重心に対応するクラスタに振り分け直す。

以下では試しにこのアルゴリズムによるクラスターの更新の様子を見てみましょう。

2. Rを用いてアルゴリズムを体験してみる

まずは、必要なライブラリをロードしておきましょう。

# 必要なライブラリのロード
library(MASS)
library(dplyr)
library(ggplot2)

まず、デモデータを次のように生成します。可視化した結果から確認できますが、今回は2次元の散布図上で2群（左下と右上）に分かれているデータを準備しました。

# デモデータの生成
X <- rbind(mvrnorm(100,c(-2, -2),matrix(c(1, 0, 0, 1), 2, 2)),
           mvrnorm(100,c(2, 2),matrix(c(1, 0, 0, 1), 2, 2)))
data <- data_frame(X1 = X[ , 1], X2 = X[ , 2])
ggplot(data, aes(x = X1, y = X2)) + geom_point()

このデータを、クラスター数K=2のk-means法のアルゴリズムによってクラスタリングする様子を見ていきます。

step 1. 各データポイントをランダムに2つのクラスターに割り振ります。

# ランダムにクラスター(culster = 0 or 1)に割り振る
data$cluster <- rbinom(n = 200, size = 1, prob = 0.5)    # 割り振り
data    # 結果の確認
ggplot(data, aes(x = X1, y = X2, colour = factor(cluster))) + geom_point()    # 結果の可視化

step 2. 各クラスターの重心を計算して、散布図上に図示してみましょう。

# クラスターの重心の計算
center <- data %>% group_by(cluster) %>% summarize(X1 = mean(X1), X2 = mean(X2))
center
ggplot(data, aes(x = X1, y = X2, colour = factor(cluster))) + geom_point() +
  geom_point(data = center, aes(x = X1, y = X2, colour = factor(cluster)), shape = 3)    # 重心を+で表現する。

step 3. 各データポイントの重心からの近さを2乗距離で計算します。この結果をもとに各データポイントのクラスターを近いほうの重心に対応するクラスターに更新します。

data$dist_cluster_0 <- (data$X1-center$X1[1])^2 + (data$X2-center$X2[1])^2 
data$dist_cluster_1 <- (data$X1-center$X1[2])^2 + (data$X2-center$X2[2])^2
data$cluster <- as.numeric(data$dist_cluster_0 > data$dist_cluster_1)
data
ggplot(data, aes(x = X1, y = X2, colour = factor(cluster))) + geom_point()

どうでしょう。綺麗に2つのクラスターにまとまったのではないでしょうか。実際にはこんなに早くクラスターがまとまるわけではないので、重心の計算・クラスターの更新を繰り返すことでクラスターをまとめていきます。

3. Rでk-means法をやってみる

Rでk-means法を実際にやってみましょう。world.pngは地球全体の夜を写した衛星写真です。

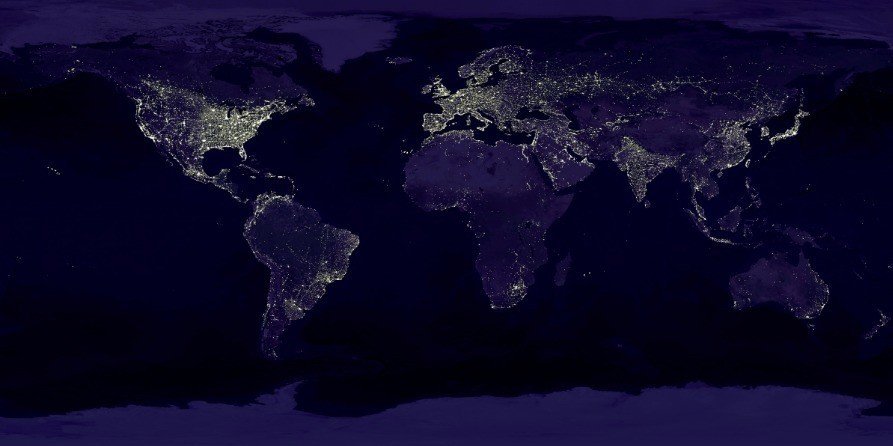
1. 必要なライブラリのロード：今回は、画像データを読み込むためにrasterライブラリを用います。事前にロードしておきましょう。

# 必要なライブラリのロード
library(raster)

2. 画像の読み込み：rasterライブラリのstack関数を用いてpngファイルを読み込んでみましょう。チャネルはRGBとalphaからなります。RGBは赤緑青の濃さ、alphaはその画像の不透明度です。

# 画像ファイルの読み込み
image <- stack("world.png")
head(x = image[], n = 5)

3. k-means法によるクラスタリング：今回はクラスター数を6としてk-means法を行い、結果を確認してみましょう。k-means法はstatsライブラリのkmeans関数で

x：データ
centers：クラスター数
iter.max：繰り返しの最大数

を指定することで計算できます。

# k-means法の計算
res <- kmeans(x = image[], centers = 6, iter.max = 100)

さて、計算結果を画像に反映させて確認してみましょう。

# 結果の確認
result <- raster(image[[1]])
result <- setValues(result, res$cluster)
plot(result)

4. k-means法のpros/cons

k-means法は他のクラスタリング手法に比べて、データポイントの数に対してスケールするという性質が知られています。そのため、他のクラスタリング手法と比較して最初に試される手法です。

一方で、k-means法には2つの注意点があります。1つはデータを標準化しておく必要性、もう一つは各クラスターのサンプルサイズの不均一性に対する弱さです。

k-means法のアルゴリズムは距離に依存しているので、ある変数の値が10倍されると、クラスタリングの結果がその変数に引っ張られてしまいます。実際に、以下のスクリプトを実行してみてください。

# k-means法のcons：各クラスターのサンプルサイズの不均一性に弱い。

## デモデータの生成
X <- rbind(mvrnorm(100,c(0, -2),matrix(c(10, 0, 0, 1), 2, 2)),
           mvrnorm(100,c(0, 2),matrix(c(10, 0, 0, 1), 2, 2)))
data <- data_frame(X1 = X[ , 1], X2 = X[ , 2])
ggplot(data, aes(x = X1, y = X2)) + geom_point()

## k-means法の計算と結果の可視化
res <- kmeans(data, centers = 2, iter.max = 100)
data %>% mutate(cluster = res$cluster)
ggplot(data, aes(x = X1, y = X2, colour = res$cluster)) + geom_point()

また、k-means法は各データポイントのサンプルサイズがおおよそ同じであるという仮定を暗に置いています。実際、以下のスクリプトを実行してみてください。

# k-means法のcons：各クラスターのサンプルサイズの不均一性に弱い。

## デモデータの生成
X <- rbind(mvrnorm(100,c(-2, -2),matrix(c(1, 0, 0, 1), 2, 2)),
           mvrnorm(10,c(2, 2),matrix(c(1, 0, 0, 1), 2, 2)),
           mvrnorm(10,c(2, -2),matrix(c(1, 0, 0, 1), 2, 2)))
data <- data_frame(X1 = X[ , 1], X2 = X[ , 2])
ggplot(data, aes(x = X1, y = X2)) + geom_point()

## k-means法の計算と結果の可視化
res <- kmeans(data, centers = 3, iter.max = 100)
data %>% mutate(cluster = res$cluster)
ggplot(data, aes(x = X1, y = X2, colour = res$cluster)) + geom_point()

次回の話

今回は分割最適型クラスタリングの代表例であるk-means法を紹介しました。k-means法は購買行動に基づく顧客のクラスタリングや胸部X線写真による肺結節の検出などに実際に用いられているクラスタリング手法です。

次回は階層型クラスタリングのうち、特に凝集型の代表例である最短距離法（単リンク法）と最小分散法（Ward法）を紹介します。

謝辞

このノートはピースオブケイクさんでの講義録です。参加者のみなさまからスクリプトのミスについてご指摘いただきました。大変ありがとうございます！