
ローマンキャピタルのプロポーションと黄金分割
さて、今回は前回の続きで、ローマの時代風のローマン体を作るおはなし。と、いうか前回のフォントに足をつけていくのだけど、これをどういう風にするかというおはなしになる。その前に基礎的な知識として、ローマン体とはどういうフォントかということは……まぁ、他でいろいろちゃんとした解説をしてくれている人が大勢いるので、詳細はそちらに譲るとして、一般に、広い意味ではJensonやGramondやPalatinoやAldusのようなルネッサンス時代のイタリアンフレーバーなフォントやTrajanのようなローマンキャピタルのみならずセリフの附いたアルファベットの活字全部がこう呼ばれているので、ローマンといわれてもイタリアにもローマにも見えないモノもあるだろうけど、今回は範囲を狭めて、古典的な書体の意味で使用している。まぁ、定義はちゃんとしないとね。

さて、一番最初の印刷機に使われていた活字は、グーテンベルクがドイツ人だったこともあってブラックレターというゴツゴツしたスタイルのフォントだったのだけれど、印刷機が欧州全土に普及してくると、このドイツな活字がどうにも気に障るという読者も増えてきた。で、イタリア人によって、この田舎臭い貧乏な活字よりも格調高いローマの活字が要求されるようになり、スビアコに移住したドイツ移民のプリースト、アーノルド・パンナーツとコンラート・スベンハイムによってキャストされたのがその最初の始まりとされている。まぁ、といっても見て貰えばわかるけど最初の頃の小文字はまだブラックレターっぽかったりするんだけど。

ただ、これは別にアーノルドやコンラートが悪いというわけではなくて、いくらイタリア人がそうはいっても、そもそも古代ローマの碑文の文字に小文字が無いじゃん……ということで、いろいろと、これでも大文字に合わせる形にグーテンベルクな活字からは大分工夫はされているから、よく見ればブラックレターよりは大分読みやすくはなっている。その後もいろいろ検討した結果、可読性などの問題でネックになっているところがだんだんとわかってきたので、別の時代の筆記体を参照したり、なんだかんだでいろいろ試行錯誤が行われ、最終的にはヴェネツィアのフランス人ニコラスことニコラ・ジャンソンによって、手書きに由来するようなデザインのボケた部分を排除してより完璧な形状、究極のプロポーション、至高の組版が完成し、もうこれ以降はブラックレターはどんどんお払い箱になっていく……みたいなことがだいたいの書体の歴史の流れになる。え? ローマン体って完成してるの? じゃあもうやれること無いじゃん……というのは、実を言えばまぁいちいちごもっともな気もするから、ここでなにかをしようとするのは無謀も良いところ何だけれど、まぁ、しばしお付き合いを。

さて、歴史を雑に説明するとそんな感じで、そこからeのバーが水平になったりセリフの形状が調整されるなどしてフマニタスがレトロニムされ、さらに18世紀半ばから19世紀以降にともなると形状はもっと合理化され、小文字のx-heightも徐々にせり上がり、さらにさらに現代ではデジタル化にともなって、より多様なアイデアと現代風の工夫がされるようにはなってきてはいるのだけれど、今回のケースではその流れに逆らっての、先祖返りしたようなスタイルのローマン体。前回作ったようなこの手の書体は分類するとオールドスタイルなローマン体の中のローマンスクエアキャピタル、通称インペリアル・ローマンなどと呼ばれるスタイルで、文字通り帝国ローマの古典的なスタイルに由来する。まぁ、そうは言ってもいま説明したみたいに現代のローマン体は全てがローマ帝国由来なので、それでは説明したことにならないうえにインペリアル・ローマンという名前のフォントが全然インペリアルではなかったりもするのだけれど……まぁ、いいか……それで、いいかたを変えればアーノルドとコンラート以降の数々の創意工夫を一旦忘れて古代のスタイルに先祖回帰したようなデザインのローマン体くらいの意味……と理解しておいてもらえればそれほど問題は無いはず……多分。

で、つまりは、結局二千年も昔の古代文字のトレースというわけなので、デザインの方向はそんな感じなのだけれど、じゃあ具体的にこれが近代的な書体とどこがどう違うのかというと、特徴を挙げるとコントラストは低めで、スラリと上品な曲線とキリッとシャープな直線にパキッと鋭いコーナー。ターミナルや終筆で墨溜まりを作らない、左右不均衡なセリフ、斜めの頂点にセリフを付けない、グリフィックな輪廓……とかまぁ色々あるけど一番大きな違いはローマの碑文に小文字が無いので小文字の書体を作らないというお約束が……まぁそれが、あることはある……のだけれど、それも、それだと現代ではいささか不便なのでローマ帝国風を掲げてはいても、小文字を作ってしまっているものもある。また、シルエットを比較して、以降のローマンと古代書体との差分を見付ける場合にはそのプロポーションを比較して……ということにもなっていて……まぁ、そのあたりは細かい話になるけど、すこしだけ解説しておこう。
アルファベットのプロポーションは大きく分けるとモダンとクラシックに分けられ、インペリアル・ローマンスタイルの大文字は……というか基本的には大文字しか無いのだけれど、その大文字はクラシックプロポーションに基づいて設計されている。クラシックプロポーションといっても細かくわけるといろいろあるけど、ローマンスクエアキャピタルはオールドもオールドで実にプリミティブなプロポーション。人文主義者に言わせると、このタイプのプロポーションの矩形は正方形をもとに定規とコンパスで作図可能な貴金属比が利用されていたと考えられていた。プロポーションシステム自体は現代ではもうかなり保守的で時代遅れなアイデアに見えるかも知れないのだけれど、古典を解釈するには有用な道具として利用でき、それをする合理的な理由も無いわけではないので、使用活用の有無にかかわらず記憶しておくと多少は役に立つ。また、これら貴金属比は現代でも工業規格始め、いろいろなものの中に深く根付いているので、デザインでも何でも実際問題として無理にここからズレたことをしようとするとバランスが悪くなってかえっていろいろとおかしな事にはなる。まぁ、今はスマホの板のサイズがいろいろと酷いことにもなっているので、大変は大変かもしれないんだけれど、基本的には世界におけるいろいろな規格を土台から作り直そうというそういう野望を抱いているのでもなければ普通はこういうところは、それに沿ってちゃんとしておかないと駄目なことにはなっている。
ただ、このことについては狂信者も多いのであんまりこういうことも言いたくは無いのだが、究極の美だの世界の全てがこの比で出来ている的なおはなしは神やサンタの実在を信じるようなもので、だいたいは壁のシミが顔に見える的な錯覚か、嘘か勘違いで出来ている。だが、しかし、そうはいっても黄金分割等々は道具としては有能なので、神だの何だのの原理主義的な勘違いさえおこさなければ現象の解釈には有用で、手っ取り早くデザインセンスを身に付けたい場合にはこういうところにもきちんと気を配るというのは当然大事ではあるのだけれどね。

で、さて、これら貴金属比の中で一番有名なのは黄金分割で……って、始めたらまたいつもの如く碌でもない雑談が長くなり、そっちが止まらなくなって話がいっこうにすすまなくなった……のだけれど……これはこれで、せっかく途中まで大量に原稿を書いてしまったので、もったいないからコラムにして文末に移動したので興味があればそちらを参照。山川龍雄ではないのでPointもReasonもExampleもPointも無いはなしなので、ハッキリ言って何の徳にもならないんだけど。
で、はなしを戻して、帝国ローマ風ローマン体のプロポーションを雑に説明するとだいたい以下のようになっている。といってもこれも諸説……というかいろいろ違うことをいう人がいるのでこれが正解というわけでは無いというか、なんというか、まぁ古代人が何を考えていたかなんてわからないので、現代人がローマ時代の碑文をトレースして勝手に言っているだけだから、個人的には判断しようも無いのでこれを誰が言っているとかは言わないけど。

あちらこちらに貴金属比に見立てた都合のよさそうなサイズが連なっているが、見て貰えばわかるようにジャンルを代表するローマンキャピタルでクラシックプロポーションのTrajanを重ねてみてもいわれるほどにはそうなっているようには見えない。まぁ実際現地に見に行けば、かの有名な碑文以外にもこの時代のモノはゴロゴロ転がっているので、全部が全部こういうことになっているわけではないということは、それはまぁご想像の通り。中には千年前からそこに建っているような顔をしているのに、よくよくみると、あ〜これっTrajanじゃねぇか! 畜生! 観光客だと思って騙しやがっってぇ! みたいな……いや、まぁ、それはいいとして、こういう考え方は人文主義の時代から始まって、みんながいろいろこねくり回した努力の結果の結晶の結論の一面もあるので、まったく無視をするというのもあまりよろしくはないから、まぁ、言いたいこともいろいろあるのだけれど、とにかく、だいたいはこんな感じに近いところに収まるように設計するというのがクラシックプロポーションの基本のキだ。モダンプロポーションに慣れているとBとかEとかSとかは大分痩せているように見えるし逆にNにはもうちょっとダイエットしろよと言いたくなるかも知れないけれど、まぁこういうのがクラシックプロポーションなので苦情は古代ローマ人に言って欲しい。それで、Trajanとかでもそうだけどこのプロポーションで作ると優雅で荘厳で美しく感じるかも……というのは……それはそうかもしれないのだけれど、プロポーションが完成しすぎていて幅の広い文字と狭い文字が混在してしまうので書体ファミリーをコンデンスやエキスパンドに拡張しようとするのには、かなり無理が生じるから、ファミリー化が前提となっているような近代的なフォントシステムにはまったく不向き……なんだけど、セリフを削ればなんとかなってしまうということなのかどうかはともかくとして、モダンなサンセリフのFuturaはこのタイプのプロポーションで設計されている。

まぁ、それもともかく、そういうことでクラシックプロポーションの特徴というのはつまりはこういうことなので、見ればわかると思うけど、文字ごとの隙間が広かったり狭かったりとまとまりが無いから、文字を組むときに全体の空間にバラツキが生じてしまい、現在のフォントデザインにおいては金科玉条の文字組における濃度の均一化という命題とはまったく相容れないので、この手の書体を近代的デザインシステムと混在させる場合は多くのケースでデザイナーは、大抵字間を広めにとってこの濃度バラツキ問題を回避しようと試みる……のだが、あぁ〜、もしかしたら、逆にそういうところが優美さや格調高さに結びつくのかも知れない。まぁ、学者ではないので、そのあたりの認知心理学的効果に関しての理解にはまったく及びもつかないのだけれど。ともかく、そういうわけなので、この矛盾や一貫性の無さを上手にコントロールすることが出来ればもちろんTrajanのような成功した書体になることはなるのだが、同様な理由で大抵の場合は盛大に炎を上げてクラッシュしてしまう。今回もそうなってなきゃ良いけど……。

さて、だいたいのフォルムが決まったらそこをストロークで埋めてしまえばフォントとしては完成する。ストロークに関しては、まぁ、ここが肝心要といってもいいのだけれど、イイ感じの真っ直ぐな線とイイ感じのカーブが引けていればイイくらいのざっくりとした駄目な説明でお茶を濁しておく。実を言うと今回のフォントは色々描いているうちに、イイ感じに捻れたカーブのS字のスパインが書けたので、まぁ、そういうことならばということで、そこから延長して文字を作っているというところが一番最初の動機になっているので、その先の作業があっちへ行ったりこっちへ飛んだりと駄目な部類に入るから、ちょっと説明し辛いという……まぁ、そういうわけで今回はわりとちゃんとしているであろうという有名なアメリカ人プリーストカリグラファーのローマンスクエアキャピタルのストロークの図を組み直して掲載したので、そっちを見て貰った方がいい。こういう感じのストロークがまさに帝国ローマンの神髄といったところでまぁ、こっちのフォントも最初のイメージで云えばこんな感じだったのだけど、やってるうちにだんだんとイメージどおりにはいかなくなっていくというところまでが、まぁお約束といえばお約束。なんでそうなってしまうのかというのは……まぁ、長くなるのでそういうところもまたそのうち。

で、まぁフォルムとストロークに関しては、ともかくそういったことで、ここまでのおはなしはいつもの如く、本題の前に余計な事をしてしまっているせいで、肝心なことが出来ていないという前回に説明し損ねた積み残しの解説といったところ。前回のフォントをダウンロードしてもらえばわかるだろうけど、プロポーションを決定し、だいたいこんな感じ……って、決めたところまで作業を進めたので、ここから先は細部をどうするかという処のおはなしになる。これが前回のフォントが何でア・バオア・クーのジオングだったのかというところの言い訳だ。そういうわけで今回は前回で一応プロポーションを仮決めしましたというところの続きから、セリフなど細部のデザインの調整を後回しにしているので、この辺りをキチンとしていこうというおはなしからが本題になるんだけど、毎回余計な事ばかりしているのでちっとも先に進まない。ホント申し訳ない。ただ、まぁ言い訳するわけじゃ無いんだけど、ここから先は細かいトコロなので、画面上での表示ではあんまり区別が付かないような部分のおはなしで大雑把にはどうでもいい……ように見えるところでもあることはあるのだが……そんなことばかりを言っているから、色んな人から怒られるのだけれど……まぁ、クリエイティブに関しては細部が大事ということもあるので、ちゃんとしようと思ったら、こういう所はちゃんとしないと全体の一貫性という目的のデザインという作業の一番大事なところが何も出来ていないと言うことにもなるので、ともかくそのあたりをどういう方針で行っているかと言うことの説明をしようというわけだ。まぁ、こんなにまわりくどい言い方になっているのでお察しかと思うけど、内容的にはコレが正解とか、こうしないといけなというおはなしなどではまったく無いということだけは保証しておく……って言うか、何というか、まぁ、毎回いうけど、だいたいいつも全部適当なことしかしてないから……ちゃんとしたことはちゃんとしたところで……お願いしますよ。ホント。

さて、それで、どういうことをするつもりかというところで話の続きは前回のおはなしの最後に示した図を再掲するけど、こういうレベルでの細部になる。このローマンスクエアキャピタルなフォント……というか、このフォント小文字を作ってしまっているのでキャピタルではないからインペリアルローマンと呼ぶけど、そのインペリアルローマンの左側のAが前回のフォントの状態で、これを右のレベルに調整しようというおはなしなんだけど画面で見ると何が違うかわからないし、実際たいした違いはないので、なんでこんなことをするのか意味もわからないだろけど、こういうところがいわゆる俗に言う細部への拘りというヤツだ。まぁ、いうほど何か凄いことがあるわけでもないのだが、その辺りを説明しよう。
インペリアルローマンはその特徴からキリッとシャープな直線にパキッと鋭いコーナーで構成されるのでこれをそのままデジタルでデータ化すると、あちこちの角で手を切ってしまうような仕上がりになる。まぁ別にそれはそれでもいいのだけれど、そういうふうにキレイに製図してしまうと過去の活字や写植の文字と違って見た目や仕上がりが大変クリアでどうにも落ち着かないし、何より目に痛い。デジタルデータ化されているモノは多かれ少なかれなんでもこの感じが付き纏うのだけれどクリアすぎる仕上がりっていうものもなんだか俺が落ち着かないので、こういう言い方はあまり好きでは無いけど、わかりやすく言えばヒューマニズムが感じられないという言い方になる。まぁデジタルにはちょっと綺麗すぎてなんとなく人を不安にさせるような冷え冷え感があるので、そういうクリーンなデータにコルモゴロフ複雑性を加味してある程度程々に温めの仕上がりに仕立てようというような調整をすれば、よりらしくなってくるんじゃないかなというわけだ。ただ、あまりに細かすぎる調整ではかえってノイズになってしまいそれはそれでまた別の意味で人を不安にさせるので、このあたりをどう塩梅するかというのもちょっと細かい差し引きが必要になる。だから、まぁ何というかちゃんと作ったモノをもう一度ぶち壊しにかかるという行為なので、やってることがパンクなだけに見えることはあるかも知れないけど、それでもまぁ何というかそういうような作業が必要にはなってくる。

上はまぁそれで、その作業をする前と、した後を比較するために細部を拡大した図で、ここまで倍率を上げればわかると思うけどもう別の文字のようになっている。このように文字の終筆や起筆に対してチョコンと取り付けられた小っちゃいストロークのことをセリフと言うのはご承知だろうけど、これがあるかないかで文字のスタイルを大まかにセリフ、サンセリフと分けるというのも、まぁこれもご承知の通り。今回はそのセリフ付きの書体を作成しているのでこういう部分の扱い一つで書体の表情も変わってくる……ということには注意を払う必要がある。
セリフはアルファベットではスタイルによっていろいろ細かい決まり事があるのだけれど、今回はそれっぽくみえればいいというスタンスなので、約束事をゴリゴリに守らなければダメというスタンスの人にはこれはこれで不満があるかもしれないけれど、まぁ、駄目な人が作っているので今回もこんな感じ。セリフはデントがあるようでないようなデザインになっている。ローマの時代のセリフのかたちはポンペイに残されていたのだが第二次大戦中に破壊され消失してしまった数少ない壁にレタリングされて遺されていたという文字の記録を見ると左右のセリフの間のデントはかなり切り込んでいてはっきりわかるほどに窪んでいる。さっきも例に出したローマカトリックのプリーストでカリグラファーのアメリカ人。エドワード・カテッチが件の円柱の文字は彫られたものではなく石にレタリングされたモノをトレースして削りだしたのだという主張している根拠にもなっている。まぁ実際石碑に彫られたモノを見るとそう言われているようにみえなくもないが、実際はデザイン上の必要性があったのか、手癖でそうなっているのか、できれば窪みはないほうが望ましかったのだがそういうわけにもいかなかったということなのかどうかとかそういうところがよくわかっているというわけではなくてあくまで推測なんだけれど。だいたいそもそもこういったセリフがアルファベットにいつから附くようになったのかということですらホントのトコロよくはわかっていないんだよね。

ただ現在は、さっきの若きプリーストがすでに第二次大戦前には考案していたという見解が一応通説とされていて、ローマ以前のギリシアの時代にそれが発明されていたとみられていることから、ローマ帝国時代にはもう附いていることが当たり前のようなことにはなっていたのだろうとは推測される。ただ、他にもいろいろなことを言う人もいるのだけれど、まぁどういう話にせよ雑に言えばセリフは文字の端っこをちゃんとする目的のために設けられている……というのが概ね常識的見解だ。というわけで日本の文字に挿入される鱗と違って当たり前だけど文字の途中に飾り代わりにセリフを設けたりはしないというのがキマリなので、繋がったストロークの途中にセリフが附いて見える場合は、そこで一旦ストロークが離れて、そこからもう一度筆が入いる……と理解される。まぁ、こういうことなのでオールドスタイルのMは一画、モダンなものは三画、もしくは四画で描かれているということになる。まぁ屁理屈を言えばね。実際はレタリングで描かれるから画数なんて関係ないけど。
と、いうわけなのでセリフには抽象的なお約束というだけではなく、実用的で機能的な側面もあって、紙質やインクが向上してくるに従って、それに伴いデザインにも変化が起きてくる。なので、わかりやすいからこの形でフォントを分類するという考え方もあって、セリフのフィレットが大きくブラケットされているものをオールドスタイル、ブラケットが最小限か全く無いものをディドーンもしくはモダーンで、その中間ぐらいのものをトランジションとざっくり三つに分け、それ以外の何といったらいいのかよくわからないものをその他の括りにして、大まかに四つのジャンルに振り分ける。また、サンセリフにブラケットの無いセリフを付けた全然ローマンじゃ無いトゲアリトゲナシトゲトゲことスラブセリフ、いわゆるエジプシャンスタイルをサンセリフではなくセリフの仲間に分類してローマン体と呼んでしまっているというケースもあったりはするので、まぁここら辺りは趣味の問題で、個人的にはどれがどうでもどうでもいいのだけれど……いや、まぁ、そんなことはともかく、今回セリフの調整がこうなっているのは、そのインペリアルローマンのデザインとそのデザインの神髄を騙った20世紀の研究の方法論を一応踏襲してはいるものの、わりと勝手に理解してこういう形にしてしまったという側面もあるから……まぁ、何回も言うけどちゃんとしたことはちゃんとしたところに尋ねて下さい。そもそもローマ人がなにをかんがえていたかというコトは俺にはよくわからないんだからね。

さて、それで作業はというと、こういうことで、最初に作ったフォントデータをこういう方針で修正していくということになることはなるのだけれど、ただ、このセリフの先っちょは、修正しようにもデザインを仮置きしている今でもかなり小さくて微妙なことになっているので、単純な形態の場合それほど問題にならないのだが、こういうケースだと小さいところで小さい変動を調整しないといけないために小さすぎてキレイにコントロールするにはユニット数が足らなすぎてちょと難しい問題になる。上のAのレフトフットセリフを超拡大した図を見て貰えばわかるけど先端はユニット数で12ユニット分の幅しか無いのだが、これでも文字の高さの六拾分の一を占有している計算になるので、細かいデザインを施そうにもさすがに整数値だけでは余裕がないからどうしようもない……ということで、じゃあその解決方法をどうするかというところのおはなしなんだけど、今回もなんだかんだで原稿量も多くなってきたので、続きはまた今度、乞うご期待。
貴金属比
黄金比は、ユークリッドの例の本では線分の外注費……じゃない外中比の問題で提示されていて、線分を二つに分かち大きい方の線分で出来る方形と小さい方の線分と全体で出来る方形の面積が等しくなるよう大小の比を求めよ……だったかな? まぁつまり、線分を外対中と中対中の比が同じになるよう分割する作図法というわけだが、このおはなしはご承知の通り「線分$${AB}$$上に点$${C}$$をとり$${AB:AC}$$と$${AC:CB}$$で比が等しくなるように線分$${AB}$$を分割せよ」という意味にもなる。ようは外と中の比率が中と中の比率に等しくなるような点$${C}$$の位置を求めよというおはなしでもあるのだが、ユークリッドのお話から$${AC}$$を$${a}$$、$${BC}$$を$${b}$$として作図すれば以下のようになる。

移項して$${b^2}$$で割って整理すれば$${(\frac{a}{b})^2-\frac{a}{b}-1=0}$$で、$${\frac{a}{b}}$$を$${x}$$とすれば$${x^2}$$の二次方程式になるので、例のあの答えが$${\frac{-b\pm \sqrt{b^2-4ac}}{2a}}$$になる公式より$${\frac{a}{b}}$$は$${\frac{1\pm \sqrt{5}}{2}}$$という答えになるから$${1}$$と、この$${x^2}$$の自然数解$${\frac{1+ \sqrt{5}}{2}}$$が求めるその比の値になる。まぁこの手の話はだいたいどこを見ても多分同じようなことは書いてあるから今更なので、今回はなるべく方程式的なものを使わない方向から解説してみよう。といってもリガには欠けるので、まぁ、説明は結構いい加減なはなしになるけど、そこはともかく。
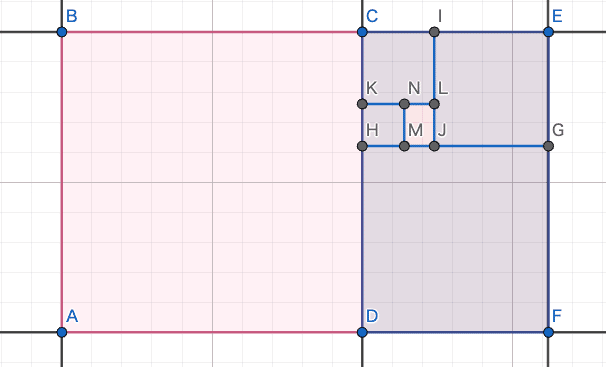
さて、もとの定義から、黄金比で作成された長方形から正方形を取り除くと残りの部分もまた黄金比の長方形になるのでこの残った部分から正方形を取り除いてもやっぱり残った部分は黄金比で作成された長方形が残るのでここから再度正方形を取り除いていくとまたまた黄金比の長方形が……という操作が無限にできる……ので、この性質を利用して小っちゃくドンドン分割したモノを全部足し合わせて合計してしまえば答えになると……まぁ、これがまさに例の等比数列の漸化式になるのだけれど、まぁわかる人にはこのあたりで何をしようとしているかがピンと来たかも知れないけど、ここでは式をあまり使わないで説明するつもりなのと、ヨビノリでも何でも無いのでこの説明を聞いたからと言っても漸化式がわかるようになったり50歳をすぎて英語がペラペラしゃべれるようになるというわけでは無い。感覚的なはなししかしないからね。まぁともかくそれで、そういうことなので図を下のように変形して$${a(a+b)}$$という面積を考えた場合、$${AB:AC}$$と$${AC:CB}$$の比が同じため$${C}$$に垂直にぶつかる線も同じ比で分割できるから、$${b^2}$$の上に空いた隙間が次々と二つの正方形の$${a^2+b^2}$$で作るL字の図形と相似で$${a}$$と$${b}$$との比で割ったサイズの形を使って順番に次々と埋めていくことが出来る……だろうということは直感的に理解出来ると思う。

さて、こういうとき古代人達はどうしたかというと、差分方程式も複素解析もライプニッツ記法もなかった古代文明ではこういう複雑な問題はお手上げになるかというと、そんなはずは無くて、この場合連分数という道具を利用して計算することが可能だった。連分数は現代人はユークリッドの互除法よりは多少ましな約分方法くらいの使い道にしか思って無い人もいるかも知れないけれど、古代では現代数学の微積分並みに高度な計算を扱うのに必要な当時の技術者にとってはもっともポピュラーで強力な道具のひとつであったのだが、あまりに高度な技量が必要でもあったので、高度な知識を継承出来るほどの能力のある人間が最終的には誰もいなくなって、これも超古代文明の誇るロストテクノロジーの一つになってしまった……って、まぁこのあたりのことはユークリッドの幾何学と違って古代の代数学、解析学を体系的に記していたかもしれないというはずのエウドクソスやディオファントスの著書が現存していなかったり多くが欠落してしまっているため、いろいろと突っこもうと思っても多分よくわからなくなってしまっているだろうから、実は適当なことを言っているだけなんだけど……ただ、なんでそういう結論に至ったのかはわからないけど答えは合ってるという連分数が見つかったりすることもあるので、古代人が我々現代人にはおよびも付かない数学理論を駆使して超巨大オーパーツを建造していたからといっても別に驚くにはあたらないということなのだけれど。


まぁ、そこはともかく、それで、この連分数での計算アルゴリズムを図にして考えると……数値を$${1:x}$$の長方形にして、その長方形から正方形を取り除き残った長方形から正方形を取り除き残った長方形から正方形を取り除き残った長方形から……と、まぁあとはこの操作を行って最後が$${1:1}$$になるまで分数の階段を降りていくというプロセスとなるので、黄金比をそれに基づいて式にすると最初の定理から$${1×x}$$の長方形を$${1^2}$$の正方形と長方形から正方形を引いた$${1x-1^2}$$の長方形に分割し両者を加算したものと考えて$${x=1+(x-1)}$$としてそれを$${x=1+(\frac{1}{x})}$$とおき、右の分母の$${x}$$に$${1+(\frac{1}{x})}$$を代入し$${x=1+(\frac{1}{1+(\frac{1}{x})})}$$としてさらに出てきた$${x}$$にも$${1+(\frac{1}{x})}$$を代入し$${x=1+(\frac{1}{1+(\frac{1}{1+(\frac{1}{x})})})}$$……とこういう操作を無限に行えるはず……と仮定すれば1だけで作るもっとも単純な正則無限連分数の$${x=1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+…}}}}}}}}}$$の結果の値に収束する。まぁ無限が出てくるので実を言うとちゃんとした証明はややこしいことになるから得意な人に考えて貰うとして、そのあたりを気にしなければこの説明のほうが感覚だけでわかった気になれる人には直感が働きやすいような気がするのでわかりやすいとは思うのだけど……どうだろう? まぁ、ともかく、それでこれを計算するのは簡単で最後の$${x}$$を$${1}$$にすれば$${1+(1÷(1+(1÷(1+…(1÷1)))))}$$って感じだからケツからアタマへウカシェーヴィチに足していけばいいだけなので答えは$${1}$$足す最初が$${\frac{1}{1+1}}$$で$${\frac{1}{2}}$$次の計算結果が$${\frac{3}{5}}$$その次が$${ \frac{5}{8}, \frac{8}{13}, \frac{13}{21}, \frac{21}{34}, \frac{34}{55}, \frac{55}{89}, \frac{89}{144}, \frac{144}{233}, \frac{233}{377}, \frac{377}{610}, \frac{610}{987}, \frac{987}{1597},…}$$精度を上げていこうとするとキリはないのでアレだけど、感のいい人ならわかると思うけどこの並びはフィボナッチ数列になっている。まぁ件の$${F_{n+2}=F_n+F_{n+1}(n\geq0)}$$の再帰計算と同じことをやってるワケだから当然と言えば当然なんだけど。というわけでフィボナッチ数の第$${n}$$項と$${n+1}$$項の割り算の結果に$${1}$$を足せば値はだいたい$${1.618…}$$あたりに収束する……と、まぁ、そういうことにはなっているので、円に円周率があり正方形が正方形であるように当然それを逆算すれば黄金比からフィボナッチ数列が出現するのは神の摂理でも何でも無いのだが、インテレクチュアルヒューミリティーの足らない人間には……いや、まぁ、そういう話はいいか。
さて、で、こんな感じで、連分数は図形を分割してデザインを設計……などという幾何的な要素と相性がいいのと、近似値への収束が速いうえに計算も四則演算がわかればいいので、大学でやるような複雑な問題でも証明の厳密性さえ無視すれば小学生にも理解できるようにしてしまえる……こともある……という利点はあるけど、周期がず〜っと一緒なら機械的に計算できるからいいんだけど普通はだいたい分母が3桁超える辺りでは約分するのも面倒に……まぁ、それはともかく、いくら時間をかけて計算しても近似値でしか求められない場合にはあちらこちらに無限がいろいろ出てくることになるので、正確な値を記号化するには残念だけど高校生でも落ちこぼれるような数学の知識は必要になる。まぁ、今回のような場合なら公式が存在していて、周期がひとつの$${n}$$、つまり分母がず〜っと$${n+x}$$のままでその分数$${x}$$の分子はこれまたず〜っと$${1}$$のままという、いわゆる正則無限連分数の場合は途中飛ばすけど結論としては$${\frac{1}{2}(n+\sqrt{n^2+4})}$$……になるので、って、合ってるよね? まぁ、こんなはなしでもしないと使う機会も無いから、ただ単純にnoteの数式記法を使ってみたかったというだけなので、ここまでのはなしでいろいろ間違っていたらごめんなさい。ともかく、それを当てはめれば答は最初に計算した値と同じにはなるはず……なってるよね? いや。まあ、それで、はなしを戻すと、この計算結果はもちろん無理数になるので、いちいち$${1.6180339887…}$$とか、或いは$${\frac{1+ \sqrt{5}}{2}}$$とか、$${Golden}$$ $${Ratio}$$とかって書くのも面倒なので、黄金比はギリシア文字の$${φ}$$で表すことにもなっていたりもする。ただ、黄金比を利用してなにかしようとするときには普通に考えても無理数では大変扱いづらいから近似値として$${1.6}$$や$${\frac{8}{5}}$$を覚えておけばいいというわけで、計算するのに連分数でも精度に全然問題は無い……多分……というわけ。ただし、$${1:φ}$$はもとの定義から結局は$${φ-1:1}$$でもあるので、それにあわせて$${φ:1}$$を$${\frac{ \sqrt{5}-1}{2}:1}$$で計算する場合もあるから、単純に数字を代入する場合にはどっちで扱っているのかの注意は必要になる。ようは長辺が$${2}$$ならば短辺はその半分の辺の正方形二個分の$${2:1}$$の長方形の対角線から$${1}$$を引いて$${ \sqrt{5}-1}$$、短辺が$${2}$$なら長辺はそのさっきの対角線に$${1}$$を足して$${ \sqrt{5}+1}$$になるって感じ。まぁ、とはいってもいろいろなところに無理数が出ることに関してのおはなしは円周率を引っ張り出すまでも無く、今みたいに作図したものを斜辺で結んだりするだけで、あちらにもこちらにもポコポコ出現するということにはなっているので、あまり気にしすぎてもどうにもならないんだけど。

さて、黄金比と並んでよく出てくる有名な貴金属比に白銀比があるのだが、この比のサイズはメジャーコードの黄金比と違ってちょっとマイナーなためどこをどういうサイズにとったものを白銀比と呼ぶのかはいろいろ諸説もある……そうなのだけれど一般的には$${1:\sqrt{2}}$$という正方形とその対角線で構成される比のことをそう呼ぶ。$${\sqrt{2}}$$の連分数も単純な形をしていて$${\sqrt{2}}$$長方形から最初に正方形を一個とるとあとは二個づつ無限に取り出せるので$${1+\frac{1}{2+\frac{1}{2+…}}}$$という形の周期1の正則な無限連分数となる。この$${\sqrt{2}}$$のサイズの矩形の長方形は縦横の長さを$${\sqrt{2}}$$倍して90度回して2つ並べると矩形が変わらずに面積が倍になるという便利な特徴があるので一枚の紙から同じ形で面積$${\frac{1}{2}}$$サイズの紙を鋏を一回入れるだけで無駄なく採寸できるから用紙サイズの規格などでも利用されている。ここからズレると、矩形を変えたくなければ鋏を三回入れて面積を$${\frac{1}{4}}$$づつにしていくか、むだに端材を出してでも無理矢理面積を$${\frac{1}{2}}$$にするかというアンチSDGsな選択を迫られることになるからだ。だから、AでもBでも美濃でも越前でも大八車でもクラウンでもだいたいこのくらいの比率にしておかないと事故を起こす。なので、まぁ、こういう当たり前のことを説明しないで、アジア人が最も美しいと感じる比率とか紙だけに神の比率だの意味がわからない頭の可笑しいことをエコーチェンバーするのはどうかと思うのだけれど、まぁ、それはともかく、それで用紙サイズのはなしに戻るとBなら1.5、A系列の場合なら1平米の用紙から始まって、さてお立ち会い、これを半分に切ると一枚が$${0.5m^2}$$のA1の紙の二枚、二枚が$${0.25m^2}$$のA2で四枚、四枚が$${0.125m^2}$$の八枚、八枚が$${625cm^2}$$で十六枚と……まぁ、蝦蟇の油じゃないんだけど、ただ実際のところは最初の最初から誤差があるので、それらが蓄積して現実には$${623.7cm^2}$$にしかならないという、まぁ理想と現実は違うのだけれど、理屈で言えばどこまで細かく切ったとしても矩形は$${1:\sqrt{2}}$$のままで近江八景白銀比は比良の暮雪か紙吹雪……。

と、そういうことはともかくとして、こんなふうに平面を良い感じに分割したいという場合に良い具合のところでオブジェクトをスケールできるから、あるていどの指標にはなるということで、こういう数値が積極的に使用されるケースもある。ただ、まぁ実際何でもかんでもこの比の値だけでガチガチに固めてしまえば絶対に大丈夫かというと、そのあたりはハッキリ言って微妙。頭の中に計算機が入っていて常に全体の比との整合性をチェックしながら作業ができるような超天才ならはなしは別かも知れないのだけど、俺も含めて大抵の凡夫にはそういうことが出来そうにないので中途半端にスケールに拘るとかえって全体の調和や整合性にたいして気がいかなくなってバランスがグチャグチャになってしまうということは往々にしてある。そもそも絶対的な美の基準なるものが存在するという考え方は一種の信仰であってそういうところに感受性が至らない人間を背教者として糾弾するという姿勢も実に狂信的で気持ちが悪い。調和やバランスを図るためにこういったものを利用しようとしているのにそのサイズに無理に収めようとして返ってバランスが悪くなると云うのでは本末転倒もはなはだしいので、まぁこういったものの用法用量はいろいろなところを考慮した上で正しくお使い下さいというぐらいの話でしか無い。だいたい、実のところ、そういうことを考慮しなくても周囲の規格の殆どがそういうバランスで出来上がってしまっていることもあって、ごく普通の感覚があれば作ったモノは放っておいても大抵はそういう枠の中に誤差で収まってしまう。だから、まぁ、こういうものをあたかも万能薬かのように喧伝して、アソコにも、ここにも黄金比などとはしゃいでしまうのは見ているぶんにはたいへん微笑ましいのだが、冷静に考えればこういう物言いは詐欺師の手口と同様で、そりゃモノの測りの当て方と、出てきた秤のメーターの誤差に対する目の瞑り方次第で、いくらでも思ったように量ることなんかは可能なのだから、流石にそういうことを偉い人が言い出すのはどうなのかとも思ったりはするんだけど、まぁ、あまりこういうことを言うのもなんだし、それはそれでみんなが愉しく幸福に信仰して生活しているというのであれば、そこに水を差す気はサラサラ無いのだけれど。
