最尤推定(maximum likelihood estimation)とは？

最尤推定は、統計学で用いられるパラメータ推定の方法の一つです。観測データからそのデータを最もよく説明する確率分布のパラメータを推定する手法として用いられます。

最尤推定の基本的なアイデアは、あるパラメータを持つ確率モデルが与えられた時、観測されたデータが得られる確率（尤度）を最大にするパラメータを見つけることです。尤度は、特定のパラメータ値におけるデータの生成確率を表しており、この尤度を最大化するパラメータが最尤推定値とされます。

この記事では、Pythonで観測データから正規分布の平均と分散を最尤推定してみます。

ライブラリをインポート

import numpy as np
from scipy.optimize import minimize

データを生成

データを生成します。平均50、標準偏差10の正規分布からサンプルを生成しました。

np.random.seed(0)
data = np.random.normal(50, 10, 100)

生成したデータを確認してみます。

import matplotlib.pyplot as plt

plt.hist(data, bins=20, density=True, alpha=0.6, color='g', label='Histogram of data')
plt.show()

最尤推定のための関数を定義

今回はSciPyの最小化の最適化関数（minimize）を利用するため、対数尤度関数にマイナスをつけます。

def log_likelihood(params, data):
    mu, sigma = params
    n = len(data)
    ll = -n/2 * np.log(2 * np.pi * sigma**2) - 1/(2 * sigma**2) * np.sum((data - mu)**2)
    return -ll

対数尤度関数は以下のように表されます。

$$
\ell(\mu, \sigma \mid x) = -\frac{n}{2} \log(2 \pi \sigma^2) - \frac{1}{2 \sigma^2} \sum_{i=1}^n (x_i - \mu)^2
$$

最尤推定

定義した対数尤度関数をminimize関数によって最小化することで、最尤推定を行っています。

initial_guess = [np.mean(data), np.std(data)]
result = minimize(log_likelihood, initial_guess, args=(data,))
mu_mle, sigma_mle = result.x

print(f"推定された平均: {mu_mle}")
print(f"推定された標準偏差: {sigma_mle}")

結果は下記の通りになります。

推定された平均: 50.59808015534484
推定された標準偏差: 10.078822447165797

また最尤推定された正規分布をプロットし、どの程度適合しているかを確認してみます。

plt.hist(data, bins=20, density=True, alpha=0.6, color='g', label='Histogram of data')

x = np.linspace(min(data), max(data), 1000)
pdf = (1 / (np.sqrt(2 * np.pi) * sigma_mle)) * np.exp(-0.5 * ((x - mu_mle) / sigma_mle)**2)
plt.plot(x, pdf, 'r-', lw=2, label='Estimated normal distribution')

plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.title('Histogram of data and Estimated Normal Distribution')
plt.legend()

plt.show()￥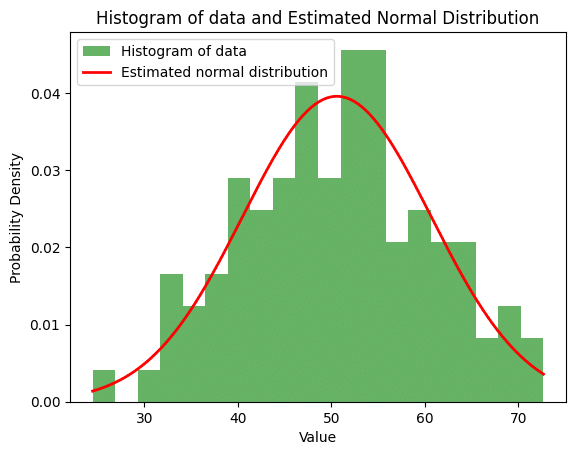

推定された平均と標準偏差は、データ生成時の実際のパラメータ（平均50、標準偏差10）に非常に近い値となっています。これは、最尤推定法が観測データに基づいてパラメータを適切に推定できていることを示しています。