Survival Analysis(生存分析)
Survival Analysis(生存分析)とは?
Survival Analysis(生存分析)は、データの中でのイベントの発生時期を分析するための統計的方法です。主に医療や生物学の分野で使用されますが、エンジニアリング、社会科学、ビジネス、金融など他の多くの分野でも活用されています。
この記事では、PythonでSurvival Analysisを行ってみます。
下記のlifelinesというライブラリを利用します。
環境はGoogle Corabです。
ライブラリのインストール
!pip install lifelinesデータセットの読み込み
lifelinesにはプリセットのデータセットがあり、load_waltons関数を使って、Waltonsデータセットをロードします。
from lifelines.datasets import load_waltons
df = load_waltons()Waltonsデータセットは、生存時間データを含むデータフレームで、以下のカラムが含まれています。
T: イベントが発生するまでの時間(観察期間)。
E: イベントが発生したかどうかを示すバイナリ変数(1はイベントが発生したことを示し、0は検閲を示す)。
group: 被験者のグループ(実験グループまたは対照グループ)。

生存分析
Waltonsデータセットで、Survival Analysisを行なっていきます。
今回は一般的な手法であるKaplan-Meier推定法を用いて推定を行います。
他にも様々な手法を用いて推定することが出来ます。
非パラメトリック手法: 特定の分布を仮定せずにデータから直接推定する手法(KaplanMeierFitter、NelsonAalenFitter)。
半パラメトリック手法: 特定の分布を仮定せず、共変量の影響を考慮する手法(CoxPHFitter)。
パラメトリック手法: 生存時間が特定の確率分布に従うと仮定する手法( ExponentialFitter、WeibullFitter、LogLogisticFitter)。
from lifelines import KaplanMeierFitter
kmf = KaplanMeierFitter()
T = df['T']
E = df['E']
kmf.fit(T, event_observed=E) 分析結果の可視化
fitの実行後に、survival_function_、cumulative_density_プロパティにアクセスできるようになります。
kmf.survival_function_survival_function_は生存関数を出力します。生存関数は、特定の時点までに生存している確率を示します。
たとえば時点15での生存確率は93.8344%。この時点までに6.1656%の被験者がイベントを経験したことを示します。

kmf.cumulative_density_cumulative_density_は生存関数の反対、つまり累積密度関数(Cumulative Density Function, CDF)です。累積密度関数は、特定の時点までにイベント(例えば死亡や故障など)が発生する確率を示します。
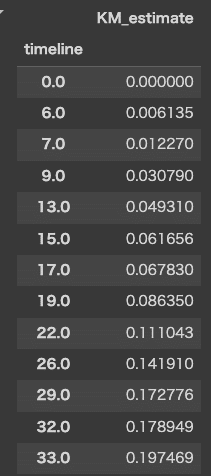
kmf.plot_survival_function()また生存関数をプロットする関数を用意されています。