ハースト指数
ハースト指数とは?
ハースト指数(Hurst exponent)は、時系列データの長期記憶性や相関性を測るために使用される統計指数です。この指数はイギリスの水文学者ハロルド・エドウィン・ハーストにちなんで名付けられました。ハーストがナイル川の洪水の研究を行っている際に、川の流れにはランダムではない予測可能なパターンがあることを発見したことからこの指数が考案されました。
ハースト指数は、一般的に $${H}$$ で表されその値によって時間系列の性質が次のように分類されます:
$${H=0.5}$$の場合、系列は完全に無相関であり、ランダムウォークに似ています。
$${H<0.5}$$の場合、系列には負の自己相関があり、将来の値は過去の値と反対の方向に動く傾向があります。
$${H>0.5}$$の場合、系列には正の自己相関があり、将来の値は過去の値と同じ方向に動く傾向があります。
Pythonでハースト指数を算出
この記事では、Pythonでハースト指数を算出してみます。
ハースト指数を算出する関数
from numpy import log, polyfit, sqrt, std, subtract
def hurst(ts):
lags = range(2, 100)
tau = [sqrt(std(subtract(ts[lag:], ts[:-lag]))) for lag in lags]
poly = polyfit(log(lags), log(tau), 1)
return poly[0]*2.0無相関
幾何ブラウン運動(Geometric Brownian Motion, GBM)でランダムウォークに基づくシミュレーションを行なっています。
from numpy import cumsum, log
from numpy.random import randn
import matplotlib.pyplot as plt
random_walk = log(cumsum(randn(100000))+1000)
plt.plot(random_walk)
plt.show()
hurst(random_walk)こちらのランダムウォークを仮定したデータに対してハースト指数を算出します。
0.4906990737245166
無相関であることを示す、$${H=0.5}$$に近いハースト指数が算出されました。
負の自己相関
mean_reversion = log(randn(100000)+1000)
plt.plot(mean_reversion)
plt.show()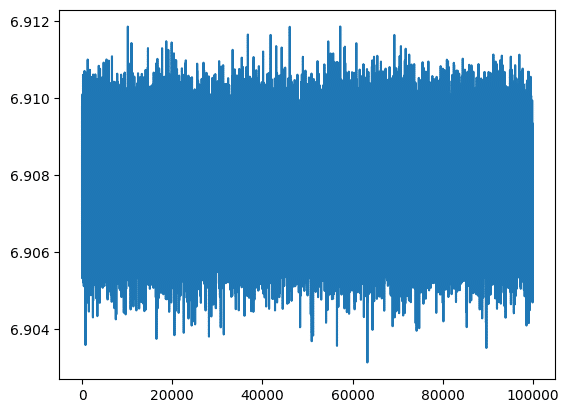
hurst(mean_reversion)-5.072840494002446e-05
$${H<0.5}$$で負の自己相関が確認されました。
正の自己相関
trend = log(cumsum(randn(100000)+1)+1000)
plt.plot(trend)
plt.show()
hurst(trend)0.9546023981308879
$${H>0.5}$$で正の自己相関が確認されました。
