モンテカルロ・シミュレーション

2024年3月18日 21:30

モンテカルロ・シミュレーションとは？

モンテカルロ・シミュレーションとはランダムサンプリングを行い、現実世界の現象をシミュレーションするための手法です。

コイン投げ

デモンストレーションとして、コイン投げで表が出る確率をモンテカルロ・シミュレーションで算出してみます。

理論的な確率としては、コインの表が出る確率は約50％になるはずです。

import numpy as np
import plotly.graph_objects as go

必要なライブラリをインポートしておきます。

n = 5000
tosses = np.random.choice([1, 0], size=n)

コイン投げのシミュレーションを5000回行います。
1を表、0を裏としてnp.random.choiceを利用してランダムサンプリングを行っています。

np.random.choiceはランダムにサンプリングするために使用されます。ここでは指定した配列([1, 0])からランダムにサンプリングされます。またサンプリングする要素の数をsizeで指定できます。

cumulative_heads_ratio = np.cumsum(tosses) / np.arange(1, n+1)

ランダムサンプリングを行ったコイン投げの結果に対して累積平均を計算して確率を求めます。

fig = go.Figure()
fig.add_trace(go.Scatter(x=np.arange(1, n+1), y=cumulative_heads_ratio, mode='lines', name='観測された確率'))
fig.add_hline(y=0.5, line=dict(color='Red', width=2, dash='dash'), name='理論的な確率')
fig.update_layout(title='理論的な確率への収束',
                   xaxis_title='反復回数',
                   yaxis_title='確率',
                   legend_title='凡例')
fig.show()

理論的な確率の収束過程をグラフで可視化してみます。

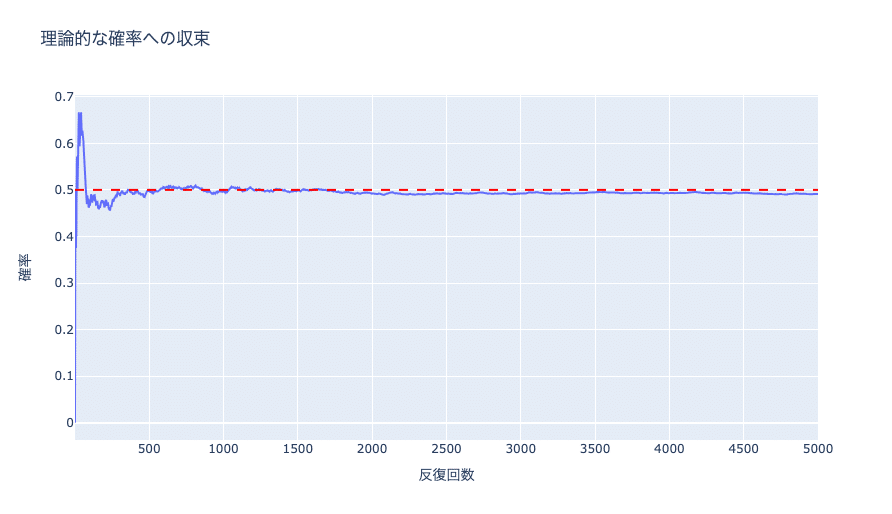
50％に収束していくのが確認できます。

株価の予測

モンテカルロ・シミュレーションで株価予測を行ってみます。
株価の推定には幾何ブラウン運動モデルを使用します。

インポート

import pandas_datareader.data as web
import yfinance as yf

yf.pdr_override()

Yahoo Financeから株価を取得するためのライブラリをインポートしておきます。

ヒストリカルデータの取得

closes = web.DataReader("7203.T", start='2023-01-01', end='2023-12-31')["Adj Close"]

今回はYahoo Financeからトヨタ自動車(7203)の株価を取得し、予測を行ってみます。2023年の1年間の日次データです。

import pandas as pd
import plotly.express as px

df = pd.DataFrame(closes)
fig = px.line(df)
fig.show()

日次リターンの計算

import plotly.express as px
import numpy as np

log_returns = np.log(1 + closes.pct_change())

fig = px.histogram(log_returns.iloc[1:], nbins=50) 
fig.update_layout(
    title='日次リターンの分布',
    xaxis_title='日次リターン',
    yaxis_title='頻度',
    bargap=0.05
)
fig.show()

日次リターンを計算しておきます。

株価の推定シミュレーション

算出した日次リターンを利用して株価の推定を行います。

u = log_returns.mean()
var = log_returns.var()
drift = u - var

幾何ブラウン運動モデルのドリフト項を計算しています。

from scipy.stats import norm

stdev = log_returns.std()
days = 50
trials = 500
Z = norm.ppf(np.random.rand(days, trials))
daily_returns = np.exp(np.array(drift) + np.array(stdev) * Z)

シミュレーション回数を500回として、モンテカルロ・シミュレーションを行います。

price_paths = np.zeros_like(daily_returns)
price_paths[0] = closes.iloc[-1]
for t in range(1, days):
    price_paths[t] = price_paths[t-1]　*　daily_returns[t]

可視化のため価格系列のデータを用意します。

推定した価格系列の可視化

import plotly.graph_objects as go

fig = go.Figure()
for path in price_paths.T:
    fig.add_trace(go.Scatter(y=path, mode='lines'))
fig.update_layout(
    title='トヨタ自動車の株価予測（50日間)',
    xaxis_title='日数',
    yaxis_title='価格',
    width=1000,
    height=600
)
fig.show()

トヨタ自動車の株価の50日間の株価予測のモンテカルロ・シミュレーションです。株価のレンジは1,903から3,754となりました。