False Discovery Rate(FDR)
False Discovery Rate(FDR)とは?
False Discovery Rate(FDR、偽発見率)は、多重比較の問題を扱う統計的手法で多数の仮説検定を行う際に、誤って「有意」と判断される偽の発見の割合を制御することを目的としています。これは、特に生物学的または医学的研究において、多数の変数に対して同時に仮説検定を行う場合に重要です。
$$
FDR=\frac{偽の発見数}{発見数}
$$
ここで、「発見数」とは仮説検定で統計的に有意と判断されたケースの総数であり、「偽の発見数」とはその中で真実ではないもの(誤って有意と判定されたもの)の数です。
この記事では、p値をランダムに生成し、FDRの制御を行ってみます。
サンプルデータの生成
p値をランダムに生成しました。
import numpy as np
np.random.seed(42)
p_values = np.random.uniform(low=0.01, high=1.0, size=100)生成したp値をヒストグラムで可視化してみます。
import matplotlib.pyplot as plt
plt.hist(p_values, bins=20, color='blue', edgecolor='black')
plt.title('Histogram of p-values')
plt.xlabel('p-value')
plt.ylabel('Frequency')
plt.show()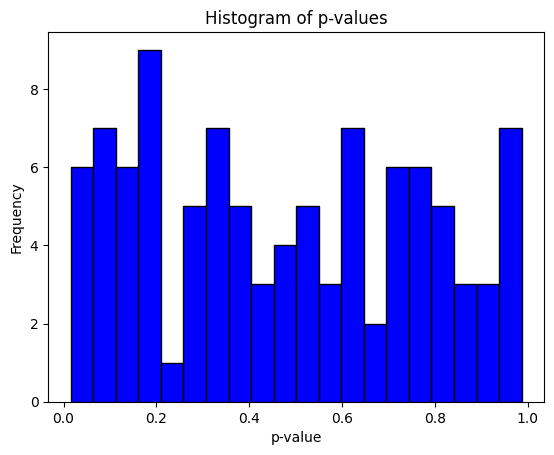
FDRの制御
FDRの制御にはstatsmodelsライブラリのmultipletestsを利用しています。FDRの制御手法にはいくつか異なる手法がありますが、今回は最も広く使われているBenjamini-Hochberg (BH) 手法を適用してみます。
from statsmodels.stats.multitest import multipletests
rejected, pvals_corrected, _, _ = multipletests(p_values, alpha=0.05, method='fdr_bh')multipletestsに設定しているパラメーターは下記の通りです。
p_values: 検定から得られた p 値のリストまたは配列。
alpha: 使用する有意水準(ここでは 0.05)。これは、許容される偽発見率の最大値です。
method: 使用する補正方法(ここでは 'fdr_bh'、つまりBenjamini-Hochberg 方法)。
multipletestsの返却値は下記の通りです。
rejected: これはブール値(True/False)の配列で、各仮説が棄却されるべきかどうかを示します。Trueはその仮説が棄却されるべきであることを意味し、Falseは棄却されないことを意味します。
pvals_corrected: これは補正後の p 値で、元の p 値に多重比較の補正が施されたものです。
今回のサンプルデータでは、rejectedの配列は全てFalseでした。どの p 値も Benjamini-Hochberg 方法による補正後の有意水準(今回は 0.05)以下にならなかったため、全ての帰無仮説が棄却されませんでした。
