
ヤバタタミンで学ぶヤジタタミ解法――ペナルティ理論
こんにちは。うまや天国です。
この記事では、「第1回シンデレラパズル総選挙」で出題したウサミンヤジタタミの解説を行います。
0. ヤジタタミのルール
①点線の上にタテヨコに線を引き、盤面をいくつかのタタミ(幅1マス×長さ2マス以上の長方形)に分割しましょう。
②矢印の数字はその方向に何枚タタミがあるかを示します。また矢印に指されている辺には必ず線が引かれます。
③数字が入るタタミのマス数は、その数字と等しくなります。
④タタミの境界線を十字に交差させてはいけません。
一応上がヤジタタミのルールです。
この記事の解説がとりあえず作者の想定している解法です。
その中で、ヤジタタミを解く上で基本となる考え(タイトルのペナルティ理論など)をいくつか説明しており、他の問題の参考にもなるようにしたつもりです。
1. ★序盤の足場組み【0~30%】
まずはルールからすぐに決まる所を進めて行きます。

まあ直ちに決まるのはこのぐらいだと思います。
例えば、緑マスの先にあるマス数はその表出数字と等しいので、その列は全部バラバラになります。
あとは、タタミは必ず縦長か横長になることに注意しましょう。
ここで、上図の黄色マスと灰色マスに注目します。
黄色の7が指す列は、最大で7枚までタタミを入れられるので、そのように決まります。
一方、灰色の7が指す列は、最少でも7枚タタミが入ってしまいます。従って、次のように決まります。

個人的な感覚では、ここまでの話がかんたん〜おてごろぐらいの難易度かなあと思います。
2. ★★ペナルティ理論【30~50%】
前の盤面から少し進みます。

ここで、上図真ん中の青マスに注目します。
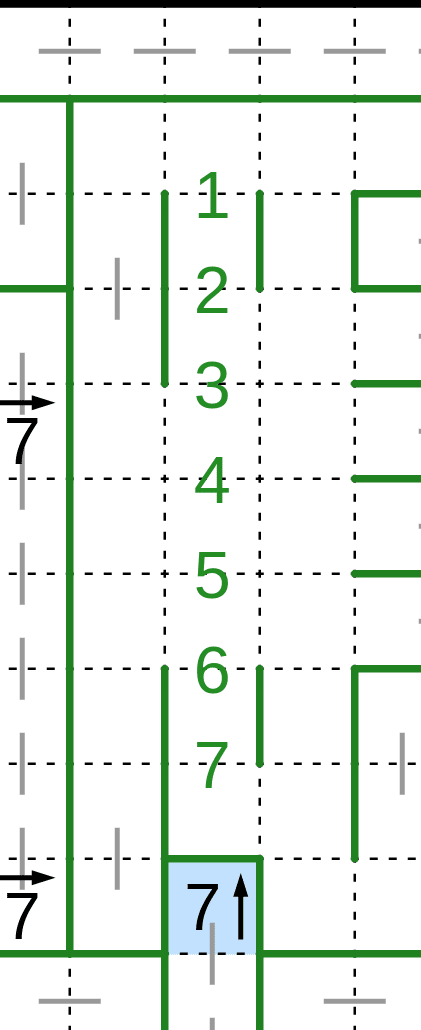
7の表出数字から、上の1〜7番の7本の辺のうち、5辺に線が引かれます。言い換えると、ちょうど2辺には線が引かれません。
ここで、もし1番と2番両方に線が引かれると、1×1の領域ができてルールに反します。従って、1番か2番のうち少なくとも一方には線が引かれません。同様に、6番か7番どちらかは線が引かれません。
以上から、線が引かれない2辺は、1・2・6・7の中のどれかになるので、それ以外の3・4・5には必ず線が引かれます。
同じ事が他の青マス2ヶ所にもいえます。

上の考え方は言ってしまえば単なるカウンティング(数え上げ)ですが、これはヤジタタミを解く上でとても有用なので、話の見通しを良くするために名前をつけたいと思います。それがタイトルにもある「ペナルティ理論」というものです。
〜〜〜【ペナルティ理論】〜〜〜
表出数字に指されている辺のうち、線が引かれないものをペナルティとよぶことにします。
このとき、タタミの枚数について次が成り立ちます。
(矢印の先のタタミ枚数)=(矢印の先のマス数)ー(ペナルティ数)
等式の例

さっきの青マス[7↑]の話は、いずれも9マス指していたので2ペナルティを持つことになります。
ペナルティの発生例

(i) 例えば、上図のように両側を辺で挟まれた部分についてA・Bのいずれかは線が引かれないので、この行の中で最低1ペナルティを生むことがわかります。

(ii) また、横向き確定の3マスタタミは、必ず2ペナルティを生みます。
この様な考え方を使うと、特にペナルティが比較的少ない表出(矢印先のマス数とタタミ数が近い、”密”な行)の制約を簡潔に表すことができるんじゃないかと思います。
〜〜〜ペナルティ理論の導入終わり〜〜〜
3. ★★ペナルティ理論適用例【50~70%】
さっきの盤面から少し進みます。

ここで、緑の7に注目します。この「7↓」の先には14マスあるので、さっきのペナルティ理論から、この「7↓」は7ペナルティを持ちます。
一方、その先にある灰色の「7←」は縦長の長さ7のタタミになるので、この縦列において6ペナを生み出します。
更に、その下の黒丸●も1ペナになります。黒丸は灰色7のタタミの内部に入れられないので、合計6+1=7ペナになります。
従って、この列のペナルティは灰色7と黒丸からしか出てきません。
また、白丸◯の付いた辺に注目すると、それぞれの白丸ペアは最低1ペナルティを生むので、さっきの議論から白丸が生み出すペナルティは灰色7が請け負わなければいけません。
以上から、

となります。
(余談:実を言うとここの話はペナルティ理論を使わなくても、上図灰色7の上辺に線を引くと破綻することが分かるので、灰色7タタミが1マス上に伸びて黄色7が発動して進みます。まあこれに気付けるのかっていうのもありますし、同じ考え方で進めればそれに越したことは無いので、こっちの解法を紹介しました。)
これにより黄色7がぴったりになるので、少し進めると

となります。
書いてから気づいたのですが実はここからのワンステップは無くても解けます。最短で解きたい方は次の3節まで飛ばして下さい。
まあこういう考え方もあるってことで参考に置いておきます。
ここで、青色7に注目すると、その列には既に横向きタタミが4枚あるので、残りのスペース的に
(緑エリアのタタミ枚数)+(黄色エリアのタタミ枚数) = 3
になります。特に、緑エリアにタタミが1か2枚しか入らないことが分かるので、ヤジタタミの「2」の手筋

から、

となります。
4. ★★★最大の難所【70~100%】

さっきの盤面から少し進めた上の図を考えます。
ここからがこの問題の最大の難所になります。
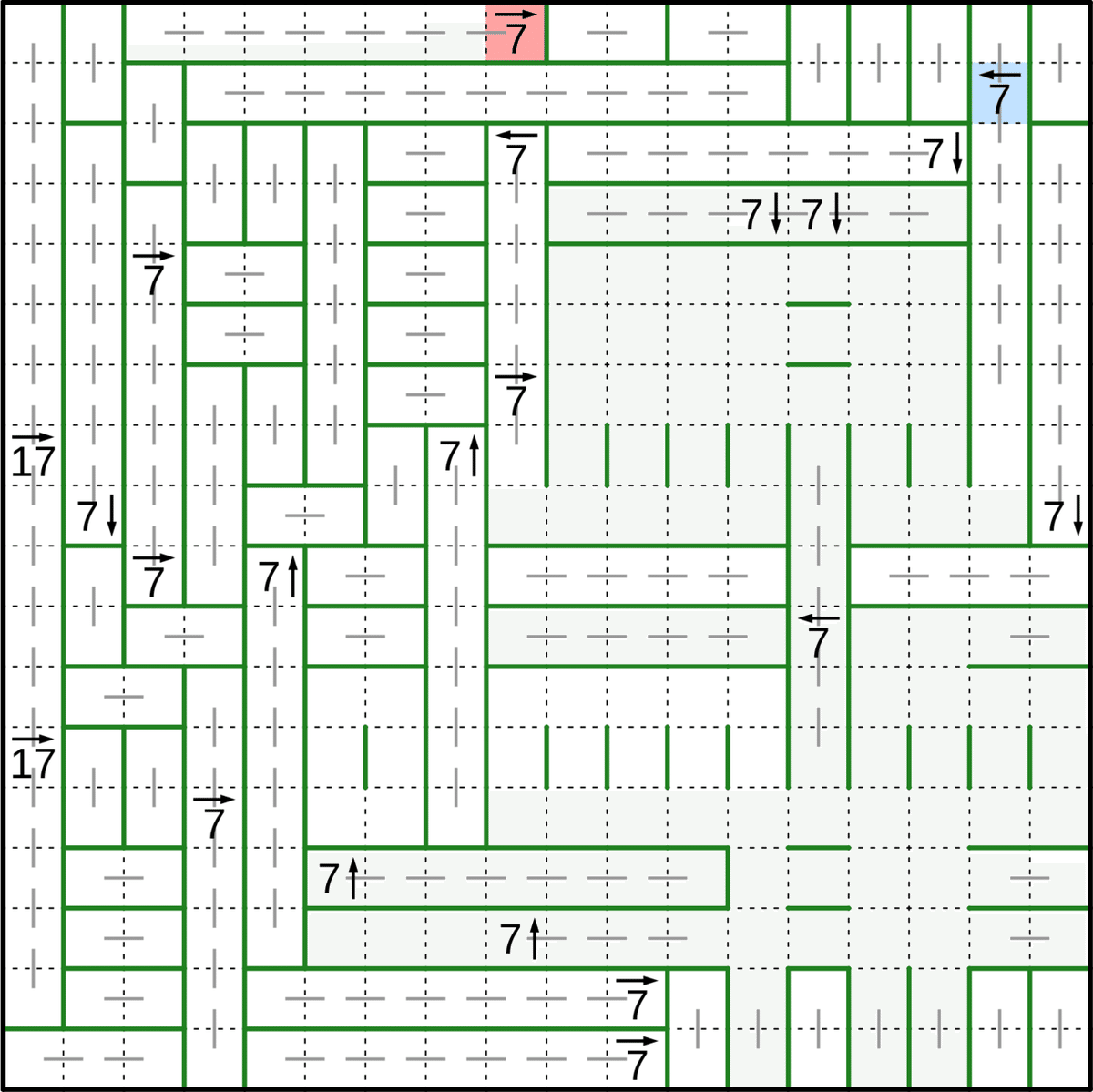
今、赤と青の2列に注目します。

☆赤7の指す列(の内まだ決まっていない部分)を見ると、8マスに6タタミ入ります。割とキツキツです。ということは、この列は縦向きのタタミをたくさん入れようとするパワーが強いと考えられます。
☆一方、一段下の青7の指す列(の決まってないとこ)を見ると、13マスに4タタミ入ります。スカスカです。ということは、この列は横向きの長いタタミを入れようとするパワーが強いと考えられます。
従って、赤7の列が持つ縦向きパワーと、
青7の列が持つ横向きパワーがぶつかり合い、
その戦いの結末こそがただ一つの答えになります!!!!!
以上のわけのわからない話を定式化します。
赤7は2ペナなので、その分け方として
(3, 1, 1, 1, 1, 1, 1) または (2, 2, 1, 1, 1, 1, 1)
の2通りあります。
また、最上段の幅1列タタミは、1×1タタミ禁により2段めにも割り込んできます。

分け方の一例(これはハタン)
最上段の縦タタミが下段に刺さりすぎて青7がハタンしている
青7の条件を考えると、最上段から刺さってきていい縦タタミは3枚までです。このことから、青7をハタンさせないような赤7の分け方は

これしかありません。
縦タタミが青7の真ん前に集まり、タタミ枚数を最小化させていることが分かります。
以上より、
となります。
あとはもうウイニングランです。これまでに出てきた「2」の手筋などを使って素直に進めていくと解けるはずです。

お疲れ様でした。
こんなサイズのヤジタタミを解く機会はそうそう無いと思います。
5. あとがき
解説は以上になります。
見ての通り難しい問題なので解けた方は本当に凄いと思います。解けなかった方もこれを機にヤジタタミに興味を持っていただけたら幸いです。
【ペナルティ理論の話】
この記事で導入したペナルティ理論は、内容的にはただの数え上げなので何か新しい手筋を創り出したりはしないでしょうが、矢印付き数字表出のパズルへ横断的に適用でき、それにより色々な手筋を議論しやすくなると思います。

例えば上のCastle Wallの場合、[1↓]が下から2行目に1ペナルティを生むので、同じく1ペナの[4→]がある程度決まります。
(ここで、Castle Wallの場合は、辺に対し垂直に線が通過しない場所をペナルティと呼ぶことにします。これはヤジタタミの"双対"チックになっていて個人的に好きです。)
【ヤジタタミガチャの話】
みゃーみゃ様のヤジタタミガチャでは、作り手の少ないヤジタタミの問題を無限に解くことができます。体感7割ぐらい理詰めで解ける問題が出るので、そういうのが好きな方には非常におすすめです。
また、(恐らく僕のせいで)「ヤジタタミ10連ガチャ」なるものも実装されており(大変助かっております)、タイムアタックもできます。この10連で時間を縮めるのにも、ペナルティ理論が便利なんじゃないかと思います。
現在のヤジタタミ10連自己ベストは13分ちょいですが、恐らく人類の限界は10分近辺なんじゃないかと個人的に考えています。競技人口がほぼいないRTAなので、世界のフロンティアを知りたい!という方は是非挑戦してみて下さい。
ヤジタタミについて解説したいことはまだまだありますが、いっぺんに大量にするのもあれなのでこの辺で終わります。気が向いたらそのうち書きます。
この記事が気に入ったらサポートをしてみませんか?
