
なぞれ!ポリオミノ
こんにちは。うまや天国です。好きなペントミノはFです。
この記事は ペンシルパズルI Advent Calendar 2021 12/19枠です。

0. 導入――いまポリオミノの形がアツい
今月発売されたニコリ177号から、ダブルチョコが定食(今後定期的に掲載されるパズル種)になり、チェンブロが二軍(定食候補)へ昇格となりました。
そんな今注目の2つは、どちらもポリオミノの形を参照するルールを持つ点で共通しており、ポリオミノの形に対する注目が高まっているという見方もできます。
ダブルチョコ:ブロック内の白マスと灰マスの形が一緒
チェンブロ:チェーン内に同じ形のブロックが入らない
ダブルチョコとチェンブロは形が持つ性質のうち「合同」をテーマにしたパズルといえますが、形の性質には他にも「相似」、「回転・反転」、「線対称・点対称」、「正方形・長方形」など様々なものがあります。
【例】
合同:ダブルチョコやチェンブロなど多数
相似:特に思いつかなかった
回転:コローン
反転:ちょうつがい、ミラーブロック
線対称:線対称・点対称、シンメトリー迷路
点対称:天体ショー
正方形:たすくえあ、るっくえあ
長方形:モチコロ、チョコバナナ
また、形といえばL字型、T字型といったおおまかな形状も考えられます。

上はL字型のペントミノ3種です。
Pペントミノだけ幅1マスじゃないのでさしがねだとアウトになってしまいますが、まあ広い意味でL字と見てしまって問題ないでしょう。
L字型ペントミノを観察すると、どれも「外周のすべての頂点が直角な6角形で、1点だけ凹んだもの」であることが分かり、そのことがL字型の定義そのものともいえます。

この例から、ポリオミノの”おおまかな形状”は外周によって判別でき、特徴づけられることが分かります。
という訳で、今回は外周の形による”トポロジカルな”分類をしてみて、どんな感じなのか見てみましょう。
★注意★
話を簡単にするため、今回は穴の開いていないポリオミノのみを考えることにします。
この条件により、ポリオミノの外周は交差のない1つのループになります。
1. ポリオミノの外周
まず、ポリオミノの外周がどのような性質を満たすのか調べてみましょう。
基本的な性質として、「全ての頂点は直角」にならければいけません。
このような性質を満たす多角形は一般に直角多角形(rectilinear polygon)と呼ばれています。
いま、内角が90°の点を凸点、270°の点を凹点と呼ぶことにすると、直角多角形について次が従います。
直角多角形の凸点の個数は凹点よりちょうど4つ多い
このことは、外周に沿って反時計回りに一周するとトータルで左向きに360°曲がることと、凸点を通る時に左に90°、凹点で右に90°曲がることから分かります。
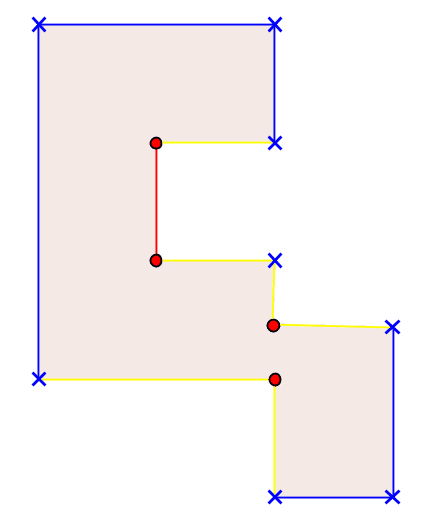
上図でいう青×が凸点、赤●が凹点です。
(余談ですが、凸点で挟まれた青辺をknob、凹点で挟まれた赤辺をantiknobと呼び、(knobの個数)=(antiknobの個数)+4 になるらしいですが別に今回は使いません)
従って、n個の凹点を持つ直角多角形はn+4個の凸点を持つため、合わせて2n+4角形になることが分かります。
特に、6角形の直角多角形(n=1)はL字型しかありません。
2. 外周の数列表示
前節で見た性質を使って、ポリオミノの外周を”おおまかな形状”によって分類する方法を考えます。
その方法として、今回はカーブデータのように辺の長さを無視し、凸点と凹点の順序で分類していきます。
いま、直角多角形は凹点の方が凸点より個数が少ないため、
外周に沿って1周する時、凹点と凹点の間に凸点がいくつあるか
を考えます。
これにより、直角多角形に対応する数列が得られるため、この数列をとりあえず凹凸列と呼ぶことにします。
【例1】適当な図形
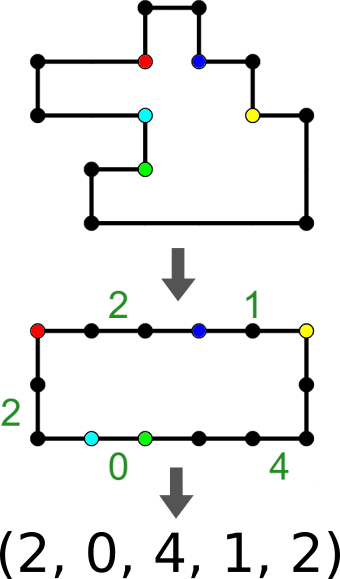
例えば、上図の直角多角形の外周を赤い凹点から反時計回りに進むと、次の凹点に着くまで2, 0, 4, 1, 2個の凸点を通って一周します。
従って、凹凸列は(2, 0, 4, 1, 2)になります。
【例2】4・6・8角形
○直角4角形、つまり長方形の時は凹点を持たないため凹凸列は()とします。
○直角6角形(L字)の時、凹点は1つで凸点は5つなので、凹凸列は(5)です。
○直角8角形の時、凹点は2つで凸点は6つなので、凹凸列は
(6, 0)(5, 1)(4, 2)(3, 3)の4つあります。
それぞれU字型、3段の階段型、T字型、S字型になります。

【例3】一般の場合
直角2n角形の時、凹点はn-2個、凸点はn+2個あるため、後述する対称性を無視すれば、対応する凹凸列はn+2をn-2個の0以上の整数に分割する分だけあります。
☆凹凸列の曖昧性
直角多角形から対応する凹凸列を求める時、どの凹点から数え始めるかによって数字の順序が変わります。
例えば、(1, 2, 4)と(2, 4, 1)と(4, 1, 2)は全て同じ直角多角形を表します。
また、反転して重なる多角形を同じとみなせば、順序が真逆の凹凸列は同じものを表します。
例えば、(1, 2 ,4)と(4, 2, 1)は同じものとみなせます。
以上より、3つの数字からなる凹凸列(10角形)の場合は、数字の順序を気にする必要はありません。数字が4つ以上になると順序を気にする必要が出てきます。いわゆる数珠順列の場合の数を数えるような感じです。
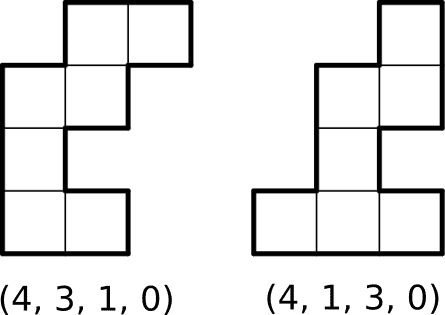
例えば、(4, 3, 1, 0)と(4, 1, 3, 0)は別の形になります。
(余談:Rectilinear polygonの論文を見てると、凹凸列と実質的に同じものであるangle sequenceというものがよく出てきますが、そちらは右左折を順に並べたもので、例1の場合(RLLRRLLLLRLRLL)となります。
ただ、長くて比較しづらいのと今回はそこまで一般的な話をするつもりもないのでとりあえず凹凸列で話を進めます)
3. ポリオミノの外周による分類
上で定義した凹凸列を用いて、色々ポリオミノを分類してみましょう。
A. ペントミノ

L字型が3つあり最多です。
Xペントミノが12角形と最大になります。
B. 10角形 or ヘキソミノ以下

ヘキソミノになると、T型(4, 2)やS型(3, 3)が多くなりました。
Fペントミノ(3, 2, 2)も急増しています。
個人的には、(4, 3, 0)のGヘキソミノとHヘキソミノが同じ外周になることが直感に反し、腑に落ちませんでした。
C. 12角形

12角形の凹凸列に対しマス数が最小なものを集めました。複数ある場合は適当に1つ選んでいます。
正直合ってるか不安なので、もしミスを見つけたら教えてください。直します。
こうしてみると、1が連続しているとマス数がかさばりがち(LRLRを繰り返すため)なことや、列に含まれる数字の最大値が小さい(うまく凹点の分布が散らばっている)とマス数が抑えられがちな雰囲気が見て取れます。
また、(3, 3, 2, 0) のポリオミノを調べている過程で面白い変形を見つけました。土下座で謝っているように見えるので”謝罪同型”と呼んでいます。

4. パズルへ応用
○ AUST
ルール
①点線上にタテヨコに線を引き、盤面をいくつかのブロックに分けます。
②各ブロックはちょうど7マスになり、アルファベットを1つずつ含みます。
③各ブロックは、その中にあるアルファベットが示す直角8角形になります(下図参照)。回転・反転・辺の長さは気にしなくてよいです。

問題

作った感想:別解が怖すぎる
○ チェンブロ[topological]
ルール
①チェンブロのルールに従います。
②同じチェーンの中に含まれるブロックは、全て対応する凹凸列が一致します。
③黒丸・白丸のあるマスはそれぞれ黒マス、白マスになります。

問題

上の問題は大丈夫なように作っていますが、一旦はブロックが穴の空いたポリオミノになるのは禁止とします。
作った感想:がんばれば何かできそう
やっぱり全体的にカーブデータと近い解き心地になりました。
5. あとがき
ポリオミノを外周の凹凸で分類することで、単なるマス数による分類とはまた違った世界が垣間見えました。
今回は触れられませんでしたが、どうしても2×2のカタマリができてしまう凹凸列((5,1)-8角形などがそうです)の条件や、穴が開いてる場合への拡張法など、まだまだ調べる余地があると思います。
個人的には、ポリオミノと同様に、直角多角形についてももっと直感的な名前が付けられたらいいなと思います。
また、rectilinear polygonで検索すると関連する研究が色々出てくるので、興味のある方はそちらもご覧になってみてはいかがでしょうか。
