
ウマヤ・ハイウェイを駆け抜けて
こんにちは。パズル大好きうまや天国です。
表題にもある通り、この記事ではウマヤ・ハイウェイという現象について調べます。
変なタイトルですが、れっきとしたペンシルパズルの話、しかもまあまあマニアックなやつをします。
1. 動機
とりあえず、まずはこの簡単なぬりみさきを解いてみて下さい。
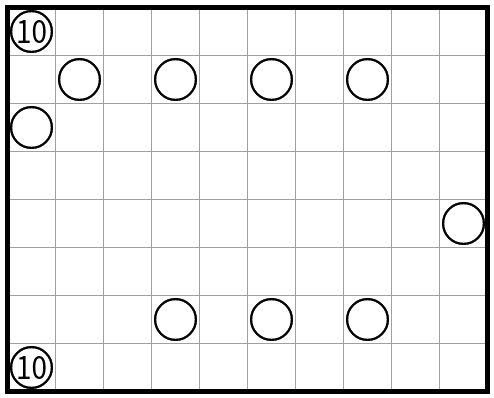
素直に解くと、最後に中央2行でうねうねしながら決まると思います。

これが

こうなる
3年前、ぬりみさきが世に出て間もない頃にこの変な決まり方を発見して面白いなと思っていたのですが、これを盤面に入れるためにはめちゃくちゃスペースを取り実用性に乏しいので、「ネタ手筋」として頭の片隅に放置していました。
そして、これと似た手筋も特に見つからなかったので、自分の中で勝手にウマヤ・ハイウェイと呼んでいました。
なぜハイウェイなのかというと、形が長い道っぽいのと、当時ペンギン・ハイウェイという映画があってそれが非常に良かったので、悪ノリで名付けました。正直関係ないです。
それから2年経ち・・・
Aqreというパズルが去年彗星のごとく現れ、ネット上で瞬く間に広がりました。
Aqreの決まり方を色々調べていると・・・?

ウマヤ・ハイウェイがあるやん!!!!
ぬりみさきとAqreでは黒白マスの制約が違うのに、同じ形が出てきました。
ぬりみさき:黒白2×2禁、岬(行き止まり)禁
Aqre :黒白4連禁、黒分断禁
特に、どちらも表出記号の無い領域が自然と一意に決まってしまうという点で一致しており、そこが興味深い点でもあります。
という訳で、この現象について調べてみましょう!
2. 定義
【ハイウェイの定義】
とりあえずどういうものを調べたいのかを考えます。
上のぬりみさき・Aqreの例では、幅2マス×長さ任意、表出記号無しの部分が勝手に決まるのが楽しかったのでした。他のパズルでも、表出が無い空白の部分がルールから勝手に決まるのって面白いですよね。
その事をふまえ、幅一定・表出記号無しの帯状領域が、ある条件下で任意の長さに対し唯一解になる様子を〇〇ハイウェイと呼ぶことにします。
帯状領域でなくても無表出領域が決まるパターン、面積に比べ異常に表出が少ないパターンなど他にも色々面白い場合はあるとは思いますが、ここではとりあえずハイウェイの場合を調べることにします。
自分で名付けといてあれですがウマヤ・ハイウェイと連呼するのは正直恥ずかしいので以後使いません。
【ハイウェイの例】

上のぬりみさきの場合、
・幅2マスの岬無し帯状領域が
・両端が黒マスと確定している条件の下
(正確には唯一解にするために追加で細かい条件がいる)
・白マスがうねうねする
様子がミサキ・ハイウェイになります。
【ハイウェイの景観】
この例では、両端黒マス確定の条件がある意味で表出の役割を果たしている気もしますが、解く前の時点では何も書いてないので、その分きれいだと個人的には思います。その傾向がある(外の情報量が少ない)ほど興味のある対象ということです。
そのことをふまえ、帯状領域の外側に必要な条件の情報量が少ないほど"自然な景観"のハイウェイと考え、なるべくそういうものを探すことにします。

定義上はハイウェイだが、矢印表出で無理やり決めてる感が強く"人工的な景観"のハイウェイ
まあこれは気持ちの問題なので、景観がごちゃごちゃしてても面白ければ何でもいいです。
3. パズル・ハイウェイを駆け抜ける
それでは、何のパズルならハイウェイを敷設できるのかを見ていきます。
通常は「パズル→手筋」という流れですが、今回は「手筋→パズル(のルール)」という逆向きの流れを見ていくことになるのではないでしょうか。
3.1【ぬりみさき・ハイウェイ】
ぬりみさきの場合、最初見たように黒マスで挟まれた幅2マス領域の間を白マスがうねうねしながら進みます。

なぜ進むのか注意深く見ると、ぬりみさきのルールの内
・白黒2×2禁
・岬禁(ルール上は全表出)
の2つがはたらいていることが分かります。白分断禁はハイウェイを進めるだけなら要りません。
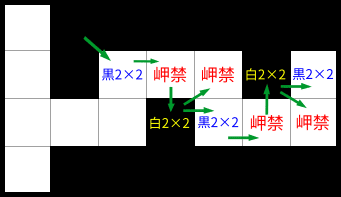
さらにこのハイウェイの仕組みを詳しく調べる方法の1つとして、次の”半ハイウェイ”が考えられます。

↓↓↓↓

2マス挟んで黒行が向かい合った段階で(+端の白2マス)、2×2禁と岬禁からこの"半ハイウェイ"が決まります。そして、半周期分のうねうね任意性が外からの条件で決まり、ハイウェイとして現れていると解釈できます。
ところで、この半ハイウェイの形、どこかで見覚えが・・・?
そうです! これは次のはしご手筋の黒白反転バージョンとも考えられます。

↓↓↓↓

白と黒は2×2禁ルールについて等価なので、岬禁がどちらの色にひっつくかで振る舞いが変わるのは面白いですね。
黒マスと違って白マスの長い列を決めるのはぬりみさきの得意分野なので、こっちの形は見たことがあるという人も多いのではないでしょうか。
ちなみにはしご手筋というのは今勝手に付けた名前なので聞いたことないと思います。
(あと、はしご手筋って何ー!?(見取り図))
3.1'【ぬりみさ木・ハイウェイ】
いわゆるぬりみさ木とは、ぬりみさきのルールに「白マスはループにならない」を足した変種ルールです。パズスクを確認した感じたぶんまどれ〜ぬさんの考案なんじゃないかと思います。
このとき、元のぬりみさきの場合と同じく幅2マスのハイウェイが出来るのは明らかですが、更に適当な条件下で幅3マスのハイウェイもできます。

ここで、右側には白マスの道が1本しかないものとします。(白マスの道が2本以上あると枝分かれする解が生まれる)
Snakeっぽいですね。
更に更に幅4マスまでいけます。

幅4マスハイウェイということは片側2車線ですね。非常に"景観が良い"と思います。差し詰めパズル界のしまなみ海道といったところでしょうか。
これを利用してやばい問題が作れます。
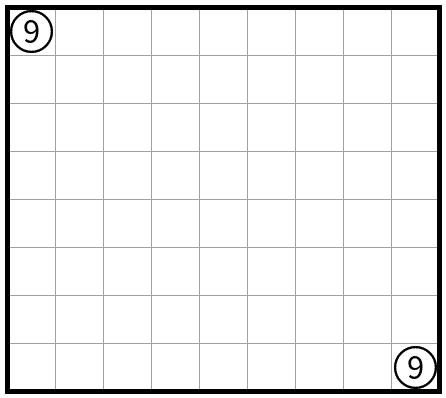
上のこれは唯一解です。こわい
さらにこれ(8×11)も唯一解です。小腸がずれます。
一般にNを9以上の奇数とした時、N×8盤面の向かい合う2隅にN岬を置くと唯一解になります。うねうね周期が4なのでこの条件だと偶数は無理です。

更に幅員を広げて5マスまでいくと道が"引き返せる"ようになるので、さすがに唯一解ではなくなります。
Uターンに3マスかかるのがこの辺に効いてる感がありますね。
広い領域にハイウェイを通す上で重要になるのは道が枝分かれしないことなので、白マスループ禁でなくても丁字路や十字路禁(or 全表出)を付ければ同じことができます。
3.2【Aqre・ハイウェイ】
Aqreの場合でも、幅2マスの領域を黒マスがうねうねしながら進む現象が見られます。この決まり方は割とよく見かけるんじゃないかと思います。

条件として、いま左右2つの黒マスをつなげたい状況で、?マスは黒白どっちでもいいのですが空行内での黒連結に関わらない状態(例えば?行内で3つ以上黒が連続していない)とします。
?行の内片方を外枠で代用すれば、実用上でも問題に組み込みやすいのではないかと思います。
このハイウェイは、
・黒4連禁
・黒分断禁
の2つが由来となります。
実際、この2要素をもつTapa [Line] (Tapaのルール+黒4連禁) でも同じことが起きます。
以前、Aqre・ハイウェイを取り入れた問題をPuzzle Squareに上げてました。実際の問題に入れるとなると、白4連禁のせいで長いハイウェイは見えづらくなりがちです。
3.3【モチコロ・ハイウェイ】
モチコロの場合、これまでとは異なる雰囲気の幅2マスハイウェイが見られます。

↓↓↓↓

炭治郎ビーム
ここで、ぬりみさき・ハイウェイと同様に上下の行は黒マス確定とします。
このハイウェイ建設に関わるルールは、
・黒2×2禁
・白マスは長方形
の2つです。白マス頂点連結性はいらないです。
この2要素をもつパズル、例えば外2×2禁付きスクリンでも同じハイウェイを建設できるはずです。
こちらも以前Puzzle Squareにモチコロ・ハイウェイを取り入れた問題を上げてました。このハイウェイはセットアップも簡単で意外と実用性が高いです。
それに似た問題を手癖で作ってTwitterの方へ上げてたので、ついでに載せときます。
3.4 その他のハイウェイ
【シャカシャカ】
シャカシャカの場合、「白マスは正方形にならない」追加ルールを付けると、幅3マスのハイウェイが現れます。

↓↓↓↓

4マスは複数解、5マスは解なしになります。
6マスになると、初期値にもよりますが上の3マスハイウェイを2倍にしたようなパターンが現れます。

「黒も正方形にならない」という訳わからんルールも足すと、6マス特有のパターンが現れます。

7マス以上は調べてません。疲れました。
逆に「白は必ず正方形になる」ルールだと多分表出を足さない限りハイウェイは作れなさそうです。
【ヴィウ】
幅2マスのヴィウの繰り返しパターンは、次の2通りある基本形を複合させたものになります。


これをうまいこと調整すると、幅2マスのヴィウ・ハイウェイを得ます。

但し、最も上の行だけ×確定という条件を付けています。
下図のように上下同じだけ×を広げることもできる・・・と思ったのですが、今度はうねうねしたパターンが出てきて唯一解になりませんでした。


盤面が縦2マスの時だとこのうねうねパターンはハタンするので存在に気づかなかった

【たわむれんが】
たわむれんがでは、黒マス分断禁ルールを足すことで、幅2マスのハイウェイを得ます。
但し、図の最下辺は盤面の最下辺とします。上はなんでもいいです。

↓↓↓↓

いつ使うねん
実用性は皆無でしょうが、この例はハニカム盤面でのハイウェイの存在を示唆しているとも考えられます。
4. あとがき
とりあえずハイウェイ構造をこんぐらい見つけましたが、探せばまだまだあると思います。やっぱりだだっぴろい空間が強い制約で一意に決まるのは良いですね。
あと、今回はハイウェイに幅一定という制約を課しましたが、もちろんその辺を緩めても面白いパターンが見つかると思います。
どんどんハイウェイを駆け抜けまくりましょう!
この記事が気に入ったらサポートをしてみませんか?
