
双対ポリスティック
こんにちは。うまや天国です。
今回はpolystickの双対を考えてみようという感じの記事です。
過去記事『振り子と円弧の気まぐれループ』と微妙に関連する部分もあるので、そちらもぜひどうぞ。
ポリスティック
定義
ポリスティック(Wikipedia)とは、長さ1の線分を端点で縦か横に貼り付けたものです。
要するにポリオミノの棒版です。
ここではちゃんとひとつながりになったものをポリスティックと呼ぶことにします。

ポリスティックが出てくるパズル
・Litherslink
・ごきげんななめ
・双子座
・イチマガ系統(そこまでポリスティック性が強くない気もする)
・7セグメント(いわゆるデジタル数字 パズルではない)
上記のものがポリスティックとしての色が強い気がします。
実際、ループ系含めタテヨコに線を引くパズル全般は、ポリスティックを配置していると考えられます。ただループ系は制限が強いのでポリスティックレベルの一般論は大して役に立たなそうです。
双対
定義
あるポリスティックに対し、各棒を中心で90°回転させたものを元のポリスティックの双対(ポリスティック)と呼ぶことにします。

・ポリスティックとその双対とで辺の数は一致
さらに、重心、線対称性、点対称性も双対で保たれる
・任意のポリスティックに対し、双対を2回とると元に戻る

・あるポリスティックに対し、必ずしもその双対がポリスティックになるとは限りません。
例えば、直進部分があるとそこで途切れてしまい、ポリスティックになりません(このような長さ1の間隙を許すものはquasi polystickと呼ばれているようです)
一般にポリスティックの双対はquasi polystickになります。
相関図
5辺以下のポリスティックについて双対関係をまとめました。
・2辺(distick)

双対によってI型は2つに分離し、L型は自身に戻ります。
・3辺(tristick)

トリスティック(棒3つのやつ)はテトロミノLITSOと対応しています。
TとOは双対、Sは自身と双対になります。
・4辺(tetrastick)

テトラスティック16種のうち、双対も連結になるものは7種あります。自身と双対なものは右側の3種あります。
・5辺(pentastick)

ペンタスティック55種のうち双対も連結なものは20種、うち自身と双対が4種です。
意外なものがペアになって面白いですね。
自己双対
定義

相関図を見てみると、他の誰ともペアにならないものがいくつかあります。
このように、自分自身が双対になるものを自己双対ポリスティックと呼ぶことにします。

自己双対ポリスティックを観察すると、「各マスにひっつく辺の数」と「各頂点にひっつく辺の数」が同じ配置をしていることがわかります。綺麗ですね。
自己双対ポリスティックの条件
では、どういうポリスティックが自己双対になるのでしょうか?
その条件を探るため、次のポリスティック→(擬)ポリオミノ変換を考えます。

ポリスティックSを斜めに倒し、各辺を対角線にもつポリオミノを対応づけます。
このポリオミノをD(S)と表し、この変換をD変換と呼ぶことにします(DはDiagonalの頭文字です)。
ポリスティックSに対し、D変換後のポリオミノD(S)は一意に定まるため、Dはポリスティック全体から擬ポリオミノへの写像となります。
※擬ポリオミノは斜め連結も許すポリオミノのことです(Wikipedia)
D変換により、ポリスティックとその双対は同じポリオミノへ移ります。 ( D(S)=D(S') )

逆に言えば、あるポリオミノの対角線を繋げてできる2つのポリスティックが、双対なもの同士のペアに他なりません。
(本当はこの方法で双対ポリスティックを定義する方が素直な気もします)
上図の通り、SまたはS'が直進するような頂点を持つ時、D(S)は擬ポリオミノにはなっても、普通のポリオミノにならない場合があります。
さらにその時、SかS'が連結になり得ないことも示唆しています。

いわれてみれば、↑のh型テトラスティックの図を斜め45°に傾けるとTミノが浮かび上がってきます。
以上より、自己双対ポリスティックの捜索は、この2種類の対角線が一致する擬ポリオミノの捜索と同値になります。
そしてそのような擬ポリオミノは、何らかの対称性を持つ必要があります。
擬ポリオミノが持ち得る対称性は以下の5つです。(群論の言葉を借りれば二面体群D4の部分群に対応)
・点対称
・線対称(タテヨコ、斜め方向)
・2方向線対称(タテヨコ、斜め方向)
・1/4回転対称
・4方向線対称(タテヨコナナメ)
それぞれ調べると、
・点対称
①回転対称が辺の中点にある時、対角線は自己双対
②回転対称がマスの中央にある時、
「対角線が自己双対⇔ポリオミノが1/4回転対称または下記④の線対称性をもつ」
③回転対称が格子点上にある時、自己双対にはならない

・線対称
④「対角線が自己双対」⇔「マスの中央を通るタテヨコ方向の対称軸を持つ」

以上から、自己双対ポリスティックの条件は次のようになります。
Sがポリスティックのとき、Sが自己双対
⇔D(S)が次のいずれかを満たす:
・点対称で対称中心が辺の中点にある
・1/4回転対称で対称中心がマスの中央にある
・線対称で対象軸がタテヨコ方向、マスの中央を通る
※「辺の中点」「マスの中央」はSの各辺をマスの対角線にもつ格子を考える
連結性
一般に、ポリスティックSに対し双対S'はひとつながりになるとは限りません。
それはSが直線部分をもつ時、D(S)でマスが斜めに接する部分ができてしまうことが原因でした。
ただ、Sが直線部分をもつからといって必ずしもS'がひとつながりにならないわけではありません。

さらに、擬ポリオミノが①~④の対称性を持てば、対応するポリスティックは自己双対になります。
実際、D(S)が擬ポリオミノになるような自己双対ポリスティックSが存在します。
このような連結性の事情もあり、自己双対ポリスティック全体の数え上げは一筋縄ではいかなさそうです。

アークループとの関係
過去記事『振り子と円弧の気まぐれループ』より、円弧からなる輪っかであるアークループは充填ポリスティックと対応していました。
そのため、ポリスティックの双対を用いてアークループにも双対を導入できます。

これを見ると、ループの線が通る円について、通らない部分のつなぎ合わせでできるループが元の双対になっていることが分かります。
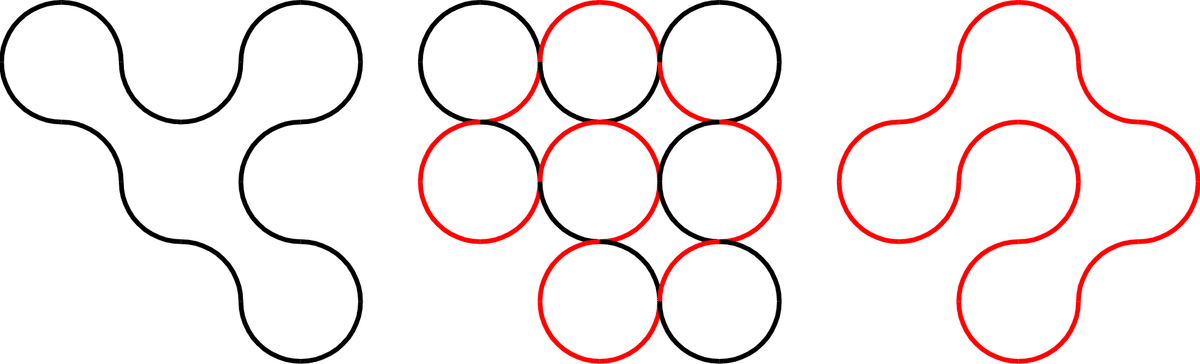
特に、逆振り子ループに対応する2種のアークループである「ゆるループ」と「うねりループ」は、この意味での双対になっています。

あとがき
今回は自己双対ポリスティックの条件を調べました。
正直quasi-polystickという用語がある時点でこの辺の先行研究はあると思っているのですが、探しても出てこないので何か見つけた方はぜひ教えてください。
この記事が気に入ったらサポートをしてみませんか?
