
パズルとデザイン
この記事はペンシルパズル Advent Calendar 2024 12/19分の記事です。
こんにちは。うまや天国です。
ペンシルのパズルは、美しい。

という訳で今回はパズルのデザイン、見た目の話をします。
書込のデザインについては過去に出ていたので、今回は表出寄りで話を進めます。
色、領域との関係
通常のペンシルパズルはモノクロのものが多いですが、色を付けることで華やかになります。特に色分けは領域系の表出と相性が良いです。

例えばダブルチョコの盤面は通常白と灰による領域塗り分けですが、めちゃくちゃカラフルにしてもいいですし、領域の境界線だけ表示してもパズルとしては同値になります。

とはいえ、解答を書き込むとさすがに一番右のは見辛いです。
境界上に線を引くパズルは色分けによる領域表示が見た目的には無難ですね。二色塗り分けできない盤面を作りたい場合は使えそうです。

ひとりにしてくれの表出数字を色に替えた例。
ひとくれはデザイン化できる高いポテンシャルを持ってそうです。
※以降の問題含め、リンクのあるものは盤面の画像をクリックすると引用元のパズスクに飛びます

シャカシャカのイラスト変種。
元ルールに領域表出はありませんが、デザイン性の高い変種に仕上がっています。

もはや塗り絵。
デジタル画面は紙面と違ってカラー印刷によるコストとか無いので、ネット上ならではのカラフルなパズルをもっと見てみたいですね。
一方で、色覚異常等で色分けの認識がかえって困難になる場合もあるでしょうし、その辺は斜線で塗り分けるとかユニバーサルデザインも必要なのかなと思います。
カラフルな表出もそうですが、R・BループやRGB美術館など、書込側も複数色を使うパズルがいくつか出てきています。こちらも今後の動向に要注目です。
図形と数学的な美
一般受けするような華やかさは無くても、整然と並んだ図形には惹きつけられるものがあります。

例えば、ポリオミノが並んでいたり、斜め線が思い思いの角度で駆け巡っていたりする風景はどこか美しさを感じます。
洗練されたシンプルなデザインがペンパの大きな特長といえるでしょう。

このシンプルさでパズルとして成立するのが凄い。
ところで、Wikipediaに数学的な美という記事があります。これは物事が持つ数学的側面の美しさを(この記事では)指していて、ポリオミノの数え上げとかへやわけの唯一解になる大部屋とからへんが当てはまるんじゃないかな〜という感じです。

幾何パズル
幾何的対象をテーマにしたパズルはいくつかあります。
(例)
○正方形:square jam、たすくえあ等
○長方形:チョコバナナ、四角に切れ等
○ポリオミノ:多数
○直交:交差は直角に限る
○平行:シンクロスケート
○鋭角・直角・鈍角:鋭直鈍ループ
○合同・相似:ダブルチョコ
○共円:共円禁のへやわけがあった気がする
まだ無いのは接線、垂線の足、五心、円弧とか?
(この辺になると格子盤面が窮屈になりそう)
まだまだ開拓しがいがありそうです。

URLは無いです(右下の半径2円弧が原因)
変種ルール:線は斜め線や円弧が通るマスを通過しますが、斜め線や円弧を跨ぎません。
ななめぐりに円弧を足してみましたが、解いてていまいち円弧である必要性が出ませんでした。
境界線またぐ回数を使うパズルならもうちょっと深みが出るかもしれません。
pzdc氏による幅広い分野の形を集めたサイト
眺めているだけで楽しい。
自由表出と連結表出
大抵のパズルは数字や黒マスしか置けないなど、表出にある程度制限があります。
一方、ナンバーリンクなど表出記号が仲間分けの意味しか持たず、(元パズルのルールで意味を持つ条件のもとで)実質何を表出しても許される「自由表出な」パズル種も中にはあります。
自由表出パズルの例
○仲間分けとしての自由表出:数独、ナンバーリンク、ひとりにしてくれなど
○対称性としての自由表出:シンメトリー迷路、シンメトリーループ
○絵:ネットワーズ、絵ヒントクロス
○文章の表出:気になるお隣さん
(クロスワードのように情報が書込の盤面と独立しているものはここでは除きます)
自由表出パズルの「何を表出してもいい」特徴は、想像以上に色々なことができると思います(表出に別のパズルを埋め込むとか)。
複数マスにわたる表出
自由表出パズルのデザインを工夫することで、表出がまとまって見えるのに実際には独立している、目の錯覚のような作問もできます。

パッと見でひとくれに見えない

過去記事からの引用
こういう連結した表出があると盤面に流れが生まれて好きなのでもっと増えてほしい。
デザインの不必要性、娯楽としてのパズル
パズルを理論的な立場から見れば、構成要素はルールと盤面から得られる条件だけであり、ただのデザインはそこに一切関与しないとも考えられます。
ではなぜ良い見た目のパズルを解いていると楽しく感じるのでしょうか。
それはパズルが娯楽の一種だからと考えています。
ただ解答を得ることだけが目的ではなく、解く過程の展開や解く前後の見た目など、様々な楽しみ方が解き手にゆだねられていることで、ルールと無関係なところにも意味が備わります。

例えば、ぬりみさきは島の先端に岬を置くパズルですが、ルール文を変えれば星雲の端に星を置いたり、道路の行き止まりに標識を置いたりと、いくらでも好きなストーリーを付けられます。
言ってしまえばこうした背景とかデザインはパズルの展開に影響せずまったく不要なわけですが、こういうのがあると解いてる時に「あ、いま島を創ってるな〜」みたいな実感が湧いてきていいですよね。
それこそがパズルの純粋な楽しみに作用し、娯楽としての"遊び"の部分を作り出しているのだと思います。
要するに面白ければなんでもいいと思います。
先週例会で配ったパズル。 pic.twitter.com/XN2AFu7Nyd
— しゑひ (@shiwehi) October 17, 2017
ルールとパズルは究極的には一致する(作:しゑひ氏)
ルール説明を提示する枠自体が問題の盤面になっており、ルールと問題が完全に融合した、パズルの1つの到達点だと思います。

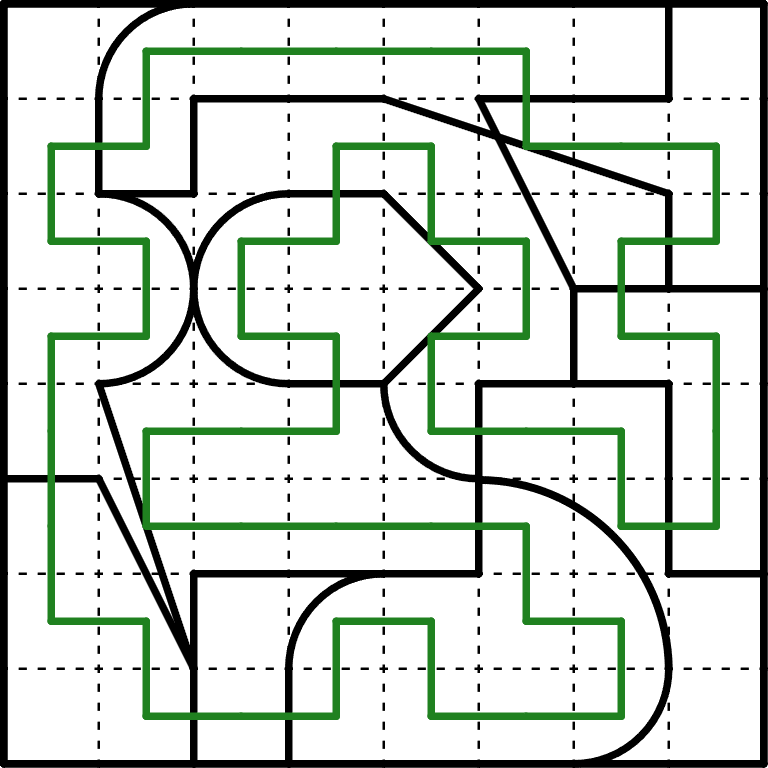
最後に、この記事用にひとりにしてくれを作りました。
手筋をそのまま表出に練りこんでみました。
パズルは娯楽である以上、既存の枠に囚われる必要は無く自由なアイデアがまだまだ生まれると思います。
デザインによるパズルの新たな付加価値、探していきたいですね。
