【読解】ファイナンス機械学習 ~第2章について~
はじめに
UKIです。
ファイナンス機械学習[1]を読んで。本書籍はフィナンシャルデータの機械学習について、データ収集からバックテストまでの一連の過程における落とし穴と対策指針を示しており、その内容は非常に共感できるものでした。ただ一部の内容について自身の知見との相違があったことも事実であり、これを取りまとめて今後に活用しようと考えました。
ファイナンスをはじめ経済学の理論というものは様々な仮定の上で議論されており、正解というものはありません。本noteの目的は書籍の内容に関して批判することではなく、読者各位が多角的な視点から内容について理解を深めることができればよいと考えています。その上で専門家からフィードバックを頂けるとこの上ありません。
本noteが好評であれば他の章の執筆・公開についても検討します。
(以下、UKIは筆者、Prado氏は著者と書きます)
読解:第2章 金融データの構造
(1)バー
書籍第2章の主旨は「金融の非構造化データの扱い方」です。ここでいう金融の非構造化データとは、すなわちティックデータ(全ての約定データ)のことを指しています。
ティックデータは生のまま利用されることは殆どなく、時系列で取りまとめたOHLCVバー(標準バー)を使うことが一般的です(株式市場の取引執行AIではティックデータを元に直後の騰落を予測していますが、特徴量としてティックデータを直接放り込むのではなく、何らかの加工をしていると考えられます[2])。トレーダーは標準バーに慣れ親しんでおり、直感的で扱いやすい反面、統計的性質が悪いという欠点を指摘されています。
書籍ではこの問題に対して、標準バーの代替としてティックバー、ボリュームバー(出来高バー)、ドルバー(売買高バー)の採用を推奨しています。これらのバーは標準バーに対して統計的性質が改善されるとのことです(IID正規分布に近くなる)。これは著者自身の主張ではなく、これまでに数々の論文が公表されています。この中で特にドルバーが推奨されています。売買高ベースとした場合、株式分割等のコーポレートアクションの影響を受けにくく経年を通じてロバストになるためです。
コラム:IIDについて
IID系列とは、各時点のデータが独立で同一の分布に従う系列であり、定常過程(強定常)の代表的な系列である。時系列分析における定常過程とは分布が時間依存しない過程であり、予測問題を扱う上で定常過程であることは必須である(時間変化するのであれば予測問題として意味をなさない)。一般的な株価の動きは当然ながら非定常(単位根過程、ランダムウォーク)であるが、その階差系列は概ね定常(弱定常)とみなして分析を行う。ファイナンスデータの時系列分析については[3]が非常に有用な書籍である。
ここではBitMEXのXBTUSDの約定データを使って標準バーとドルバーの比較を行いました。対象に仮想通貨を選定した理由は以下の通りです。
・株式だと銘柄毎の特性が大きく異なるため結果を集約しづらい
・FXは約定毎のデータが取れず出来高も分からない。
・仮想通貨は株とFXの中間のような特徴を持っている。複数取引所で構成され裁定による価格調整圧力が働く。FXのような相対取引でなく株のような板取引である。BitMEXは世界一の出来高を誇り、BTC価格のリーディング取引所となっている。メイカーテイカー手数料制を導入しておりティック幅が適切で板が厚くキューの概念がある。
結論として標準バーに対してドルバーのほうが統計的性質が大きく改善します。これは以下のヒストグラムを見ても明らかです。数値的な評価指標として、正規分布を仮定した場合の最尤推定結果(平均、標準偏差)の時間推移を観察しました(時系列で一定に近いほうが良い)。ドルバーのほうが特に標準偏差の推移が安定していることが分かります。

リターンヒストグラム
(左:標準バー、右:ドルバー)

平均および標準偏差の時系列推移
(赤:標準バー、青:ドルバー)
この統計的性質の改善がどれくらいモデル精度に影響を与えるか、現時点では不明瞭です。一般的に標準バーでの分析は異常値は除去して考えるため、分布のテールは気にならないことが多いです。またドルバーの場合、バーの形成期間が非常にバラつくことも分析上の課題だと考えています。今回の検証ではドルバー1224本中、MIN期間は2sec、MAX期間は818secでした。
一方、このようなサンプリング間隔によるリターン分布の整形手法は、極端な話、後述するCUSUMフィルタのようにリターンの幅を固定としてサンプリングを行う手法を用いると任意の形に整形できてしまいます。サンプリングを用いて恣意的なリターン分布整形が行われた場合、統計的エラー(バイアス)への影響も検証する必要がありそうです。
(2)Information-Drivenバー
書籍ではドルバーからさらに踏み込んだInformation-Drivenバーが提案されています。これはボリュームインバランスバー、ボリュームランバーなど、売買サイドの偏りを考慮したバーの作り方です。仮想通貨で高頻度botを製作している方々には周知の事実ですが、ボリュームインバランスは短期的な価格の値動きを説明するための代表的な指標であり、日本でも文献が多数見られます[4]。これらのバーは書籍で著者自身が提唱しているものであり、書籍出版以前には関連研究がなく、かつ具体的な改善効果の記載はありません。著者は2010年に発生したフラッシュクラッシュに関してVPINをはじめ、いくつもの論文を執筆しており、この辺りの知見からInformation-Drivenバーの有用性を考案したものと考えられます。
高頻度bot製作の際には是非とも研究したい材料です。実運用の際にはデータ取得から演算、執行までの高速性が要求されることは言うまでもありません。
(3)特徴量サンプリング
書籍では機械学習のターゲットをリターンを元に3つのラベルに分割する方法(3値分類問題)をベースとしています。しかし分類問題において、ある閾値を元にターゲットを分割してラベリングする場合、各ラベルのサンプル数が偏ると恣意的な結果を招いてしまいます(不均衡データの問題)。
コラム:不均衡データの問題
例えば極端な話、ラベル1(騰落率が+20%以上)、ラベル0(騰落率が-20%~+20%)、ラベル-1(騰落率が-20%以下)とした場合、ラベル0に99%のサンプルが偏ることになる。この場合は何も考えずにラベル0を予測結果とすると、予測精度は99%となってしまいうまく学習ができなくなる。詳細は[5]参照のこと。
このような不均衡なラベリングを行う場合、それぞれのサンプル数が極力等しくなるよう、多数派のラベルについてダウンサンプリングを行います。
書籍でもリターンの値幅を固定してダウンサンプリングに関する手法(CUSUMフィルタ)が紹介されています。ここでダウンサンプリングの理由として「SVMなどの機械学習アルゴリズムは大きなサンプルサイズにたいして機能しない」、「機械学習アルゴリズムは適切なサンプルで学習を行うと最高の精度に達する」との記述があり、この辺りの事情がよく理解できませんでした(単純にリターン分布を2値に固定するためだけの処置だと筆者は考えています)。
一般に統計分析においてサンプル数は重要なパラメータです。サンプル数が少ない場合、統計的エラーの発生頻度が大きく上昇してしまいます(下図)。このことは文献[6]にも記載があります。また、ダウンサンプリングについては予測確率にバイアスが生じるとの報告例もあり、予測確率にカリブレーションが必要となる可能性が高くなります[7]。どちらにせよダウンサンプリングを行う際には適切なサンプル数が残るよう閾値の調整が必要となるでしょう。
また、値幅の変動が起きた場合のみ考えるCUSUMフィルタに対して、値幅の変動が発生しなかった場合も考慮に入れる通常の分類手法にも優位性は存在すると考えています。
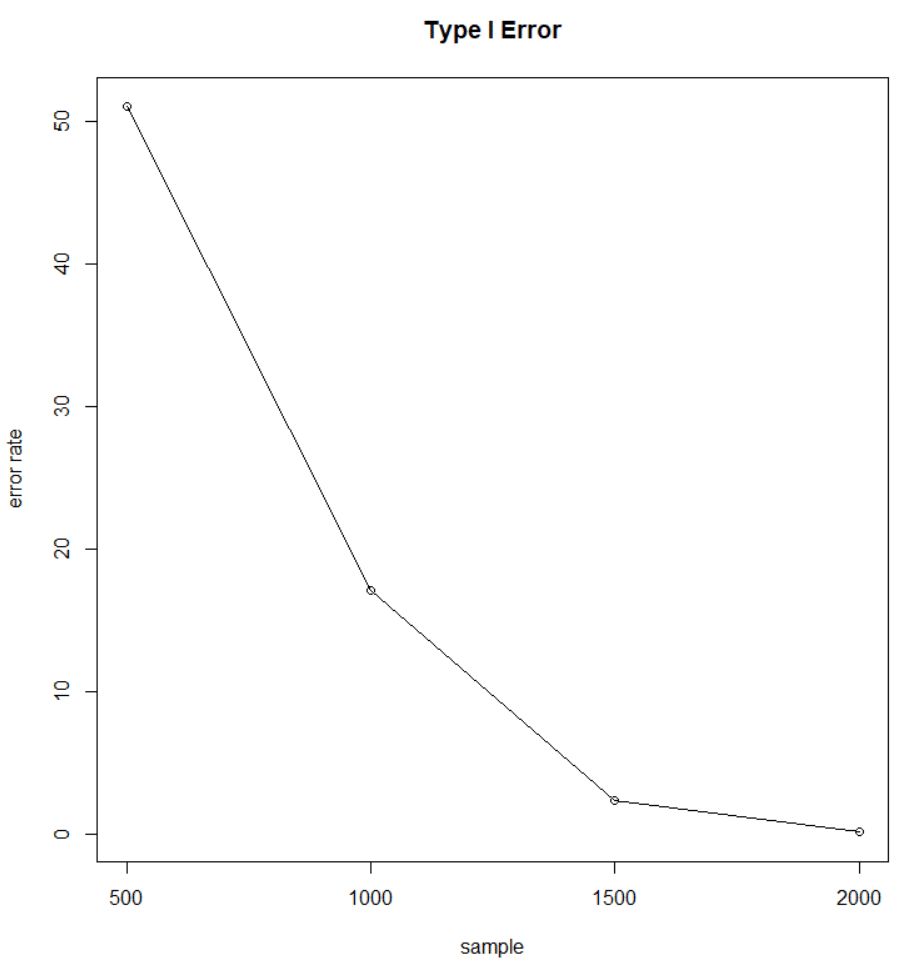
サンプル数と統計的エラーの発生頻度
おわりに
ファイナンス機械学習の第2章では、金融非構造化データのサンプリングに関するテクニックが説明されていました。この章では、リターン分布形状を改善(というより整形)する方法(正規分布に近づけたりラベリングのために強制的に2値化する手法)に触れられました。これは機械学習に適したターゲットを生成する一方で、サンプリングに恣意性が介在するとバイアスへの影響が懸念される、バーの形成期間に大きく不均衡が発生するためその他の特徴量への影響が不透明となる、実際の運用ではデータ取得、演算、執行まで高速性が要求されるためアルファの回収が難しくなる、ダウンサンプリングでは予測確率にバイアスが生じる可能性がある、などのデメリットも考えられます。
以上の考え方より、機械学習に適したターゲットの生成は様々な問題とのトレードオフであると考えています。とある人が「一般的な時系列データ予測の問題は非定常過程との戦いなので、本質的に定常過程を想定する機械学習手法での予測は計量時系列分析など非定常過程も考慮した古典的なモデルによる予測には及ばない」と述べたのを思い出しました。
ファイナンス機械学習はまだまだこれからの分野であり、様々な側面から検証を進める大切さを改めて実感した次第です。
参考文献
[1]ファイナンス機械学習 Marcos Lopez de Prado
[2]トレーディングフロアーでのAI業務 みずほ証券
[3]経済・ファイナンスデータの計量時系列分析 沖本竜義
[4]執行戦略と取引コストに関する研究の進展 杉原慶彦
[5]機械学習における不均衡データの扱い方
[6]テクニカル分析の迷信 David Aronson
[7]ダウンサンプリングによる予測確率のバイアス
