シストレのススメ第3回 ストラテジーの設計方針
さて、リターンの期待値e、標準偏差σ、トレード数Nですが、それぞれがどういう関係を持つか、把握しておく必要があります。
1.トレード数と期待値の関係
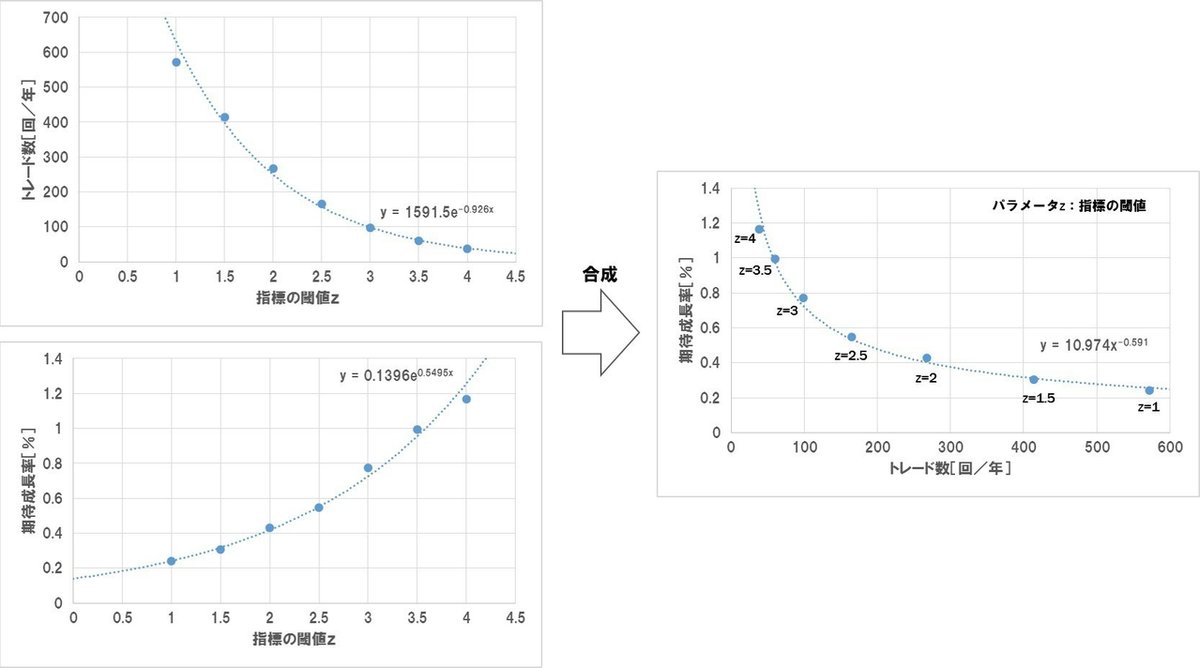
まずトレード数Nと期待値eの関係に着目します。左下図はあるストラテジーについて、売買条件の閾値zを変化させてトレード数と期待値の関係をプロットしたものです。
このグラフを見ると、トレード条件を厳しくしてトレード数を絞った場合、線形的ではなく累乗関数的(つまりy=c×x^α、cとαは定数)に期待値が向上することが分かります。どのようなストラテジーの指標を使っても同様の特性を示すはずです。もしグラフの形が歪む場合(累乗関数で近似しようとすると掛け離れる場合)は、そのストラテジーは過剰最適化(カーブフィッティング)されている可能性があります。もしくはストップロスなどの設定で分布の一部を強制的に刈り取っている場合です。
この特性が累乗関数的となるのには数学的な理由があります(章末に説明を記載しています。やや専門的な内容となるので読み飛ばしていただいて構いません)。
さて、プロットしただけでは何処のポイントがパフォーマンスに優れるか判断できません。従って、このグラフ上に「総利益の期待値」の等高線を示しました(右下図)。総利益の期待値=N×eであることから、等高線の式は、e=A/N(=A×N^-1、Aは定数)となります。この等高線に対して右上に行けば行くほど、パフォーマンス(ここでは総利益の期待値)が向上します。同じライン上では、パフォーマンスが同等になります。
等高線の曲線はe=A×N^-1であるのに対し、ストラテジーの曲線はe=c×N^α(0>α>-1)となっているため、トレード数Nが増えれば増えるほど、等高線に対して相対的に「総利益の期待値」曲線が上昇します。つまり、このストラテジーで売買条件の閾値を調整して総利益の期待値を増やそうとした場合、期待値を犠牲にしてトレード数を増やしたほうが理論上有利となります。ただし期待値が低くなると、期待値を阻害する要因から受ける影響が大きくなります。これについては、次回以降で詳細に説明します。

2.期待値と標準偏差の関係
では次に期待値eと標準偏差σの関係を見てみましょう(左下図)。
前回のトレード数と期待値の関係と同じく、こちらの関係も累乗関数的となり、σ=c×e^βと表すことができます。ただし、前回と異なるのは、累乗係数が前回は(0>α>-1)であったのに対して、今回は(0<β<0.5)の範囲となっています。
さて、何処のポイントがパフォーマンスに優れるか判断するため、今度はこのグラフ上に「最大DD」の等高線を示しました(右下図)。最大DD=9/4×σ^2/eであることから、等高線の式は、σ=B×SQRT(e)(=B×e^0.5、Bは定数)となります。この等高線に対して右下に行けば行くほど、パフォーマンスが向上(最大DDが減少)します。同じライン上では、パフォーマンスが同等になります。
等高線の曲線はσ=B×e^0.5であるのに対し、ストラテジーの曲線はσ=c×e^β(0<β<0.5)となっているため、期待値eが増えれば増えるほど(つまりトレード数Nが少なくなればなるほど)、等高線に対して相対的に「最大DD」曲線が小さくなります。つまり、このストラテジーで売買条件の閾値を調整して最大DDを減らそうとした場合、トレード数を絞って期待値を高めたほうが理論上有利となります。期待値が高いストラテジーを採用したシステムが、ドローダウンの小さい堅牢なシステムであると言えます。
総利益の期待値の観点からはトレード数を増やしたほうがよく、最大DDの観点からはトレード数を減らしたほうが良いことになります。では結局どちらが有利なのかを、運用レシオを対象に見ていきたいと思います。

3.トレード数とシャープレシオの関係
最後にトレード数NとシャープレシオSRの関係に注目します(左下図)。
シャープレシオは期待値e/標準偏差σです。トレード数Nに対して期待値eと標準偏差σはそれぞれ累乗関数的な特性を示すため、e/σの値も累乗関数的となります。式で表すと、e=A×N^α、σ=C×N^γのため、SR=A/C×N^(α−γ)=c×N^δとなります。
ストラテジーの総合パフォーマンスを見るため、このグラフに「運用レシオ」の等高線を示します(右下図)。運用レシオ=4/9×N×SR^2であることから、等高線の式は、SR=D/SQRT(N)(=D×N^-0.5、Dは定数)となります。この等高線に対して右上に行けば行くほど、パフォーマンス(運用レシオ)が向上します。同じライン上では、パフォーマンスが同等になります。
等高線の曲線はSR=D×N^-0.5であるのに対し、ストラテジーの曲線はSR=c×N^δ(0>δ>-0.5)となっているため、トレード数Nが増えれば増えるほど、等高線に対して相対的に「運用レシオ」が向上します。つまり、このストラテジーで売買条件の閾値を調整して運用レシオを増やそうとした場合、トレード数を増やしたほうが理論上有利となります。

4.では一体どう設計すべきか
(1)ストラテジーのパラメータδ
さて、ここからが問題です。トレード数に対するシャープレシオの感度を表すδについて考えます。δの値はδ=α−γであり、αはトレード数に対する期待値の感度、γはトレード数に対する標準偏差の感度となります。さらに言えば、αはストラテジーに採用する指標の期待値の分布、γはストラテジーに採用する指標の標準偏差の分布から決まります。つまり、結局パラメータδは「ストラテジーに採用する指標」によって決まります。このδの値がどのようなものが望ましいか考える必要があります。
(a) δ≧0の場合
これは物理的にありえません。この場合はトレード数を大きくすればするほどシャープレシオも向上することになってしまいます。そのような夢のような指標は見たことがありません。
(b) 0>δ>-0.5の場合
これは今回の代表例と同じです。この場合、期待値を犠牲としてトレード数を大きくすればするほど、パフォーマンスが向上します。カウンタートレンド(逆張り)系の指標がこれに当てはまります。
(c) δ<-0.5の場合
この場合、トレード数を絞って期待値を高くすることでパフォーマンスが向上します。トレンドフォロー(順張り)系の指標がこれに当てはまります。
(b)の指標を採用する場合、トレード数を大きく設計すべきです。(c)の指標を採用する場合、トレード数を小さく設計すべきです。では一体、どちらが有利となるのでしょうか。
(2)トレード数の効用をもう一度考える
運用レシオが同等の場合、トレード数の多寡について優劣を見てみます。運用レシオが同等のストラテジーAとストラテジーBを考えます。それぞれのストラテジーについて、単位期間当たりのトレード数をNa、Nb、期待値をea、ebとします。単位期間運用した場合の総利益の期待値は両者で等しくなるため、
Na×ea=Nb×eb
であり、この式を変形すると、
eb=(Na/Nb)×ea
となります。これらのストラテジーで一定期間複利運用したときの総利益の期待値は、
ストラテジーA:(1+ea)^Na-1
ストラテジーB:(1+eb)^Nb-1=(1+(Na/Nb)×ea)^Nb-1
ここでトレード数の比Na/Nbをαとおくと、
ストラテジーA:(1+ea)^(α×Nb)-1
ストラテジーB:(1+α×ea)^Nb-1
となり、ストラテジーAが優秀であるためには、
(1+ea)^α>1+α×ea ・・・①
を満足する必要があります。ここで、①式の左辺をマクローリン展開すると、右辺がその第1項および第2項となります。従って、
(1+ea)^α=1+α×ea+・・・
となり、α>1の場合(つまりNa>Nbの場合)には、必ず①式が成立します。
よって運用レシオが同等でトレード数の異なるストラテジーを比較すると、複利運用の観点からトレード数の多いストラテジーのほうが優れます。従って、トレンドフォロー(δ<-0.5)のストラテジーでトレード数を絞り期待値を高めて目標の運用レシオを達成するよりも、カウンタートレンド(0>δ>-0.5)のストラテジーで期待値を犠牲としトレード数を稼いで目標の運用レシオを達成したほうが、より効果的であると言えます。
今回は複利運用の場合を考えましたがこのように考えなくとも、δ≧0のストラテジーが物理上ありえないほど良好なパフォーマンスを示すため、δの値が0に近いカウンタートレンドのストラテジーのほうが本質的に良い(システムトレードを運用して短期間で効率的にお金を稼ぐ上で、という意味です)ことは疑いようがないのです。
5.まとめ
つまりここまでを要約すると、システムトレードのストラテジーの設計方針(どのような指標を採用してどのようにe、σ、Nを設計するか)として、
1.「カウンタートレンド系の指標(0>δ>-0.5、0に近いほうがベター)を採用し、トレード数Nを極限まで大きくする」という戦略に優位性があります。
2.このとき、上記の戦略に伴って低下する期待値eに対して、「どれだけ期待値の阻害要因を排除することができるか」ということも取り組むべき問題の1つです
「期待値を犠牲にしてでもトレード数を増やす」といったことは反論が多いと思いますが、実トレードにおける事情はさておいて、理論的には正しいと考えています。次回からはトレード数を稼ぐ上での注意点と、成長率の阻害要因をどうケアすべきか説明していきたいと思います。
--------------------------------------------------------------------------------
<参考:Nとeの関係が累乗関数となる数学的根拠>
ここではトレード数と期待値の関係が累乗関数的(つまりy=c×x^α、cとαは定数)となる理由について説明します。やや専門的となるため、本記事は読み飛ばしていただいて構いません。あるストラテジーについて、売買条件に含まれる指標の閾値zを変化させた場合のトレード数やリターンはその指標に対して市場そのものが持つ分布の一部を切り出したものとなります。例として、上記のグラフを得るために変化させた指標に対するトレード数の分布を見てみます。

この分布は正規分布です。どのような指標であれ、市場そのものが持つ分布は自然界で形成される分布(正規分布や対数正規分布)に近い形となります。正規分布の公式は、
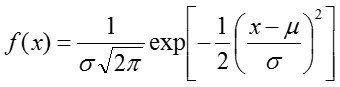
であり、この分布に対してある一定の閾値zより上(もしくは下)のトレードを抽出することになります。このときのトレード数は正規分布の上側確率の式となり、下記の積分で表されます。
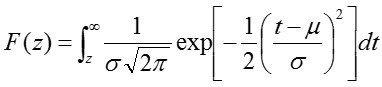
この式は、通常の積分公式では解くことはできないため、数値解析的に求めるのが一般的です。ただし、積分される元の式にはexp関数が含まれており、当然積分した後にもexp関数が残ります。従って、この積分結果は指数関数式で最もよく近似することができます。今回の代表例を見ても、指数関数での近似が上手く働いていることが分かります(下の図を参照してください)。このとき、近似的に指標の閾値zに対するトレード数Nの関係は、
N≒Aexp(az)・・・①
で表されます。同様のことは、期待値にも当てはまります。同じく、指標の閾値zに対する期待値eの関係は指数関数で最もよく近似され、
e≒Bexp(bz)・・・②
式①と式②を使い、eとNの関係を表すと、
e≒B×A^(-b/a)×N^(b/a)
となり、期待値eはトレード数Nの累乗関数で近似的に表すことができることが分かります。