
AIを使った儲かる自動売買の見分け方 ~トレーディングのバイアス対策技術の歴史と展望~
0.はじめに
UKIです。
主題と副題の序列を迷いましたが、いったんPVを稼げそうなほうを主題に置きました(そのうち修正します)。
(1)対象読者
・EAやbotなどの自動売買に興味がある方
先に結論を書いてしまいますが、たとえAIを使ったとしても儲かる自動売買の戦略を完全に見分けることは不可能です。
商材自体は悪いものではありません。当然、製作者が誠意をもって製作したものもあるでしょう。しかし現実には、悪意のあるもの(儲からないと分かっているが儲かるように振る舞っているもの)や、悪意はなくともバイアスに気付いておらず、結果として購入者が不利益を被るものが大多数紛れ込んでいます。
そもそも市場にアルファ(収益の根源)は殆ど存在しておらず、自動売買の戦略構築過程で発生するバイアスの影響を掻い潜って将来的に利益が出る戦略を作る(見分ける)のは極端に難しいことを知るべきです。不特定多数に販売されている戦略で簡単に利益が出ると考えるのは、明らかに間違っています。
本記事は、少しでも自動売買に関するリテラシー向上に寄与することを願い、無償にて公開するものです。初学者には難しい内容であり、1章と4章のみ読めばよいと思います。特に1章を繰り返し読み、自動売買の戦略構築の本質がどのようなものか理解して頂けたら良いと思います。
・EAやbotなどのトレーディング戦略を構築している方
トレーディング戦略の構築における過剰最適化に関する注意喚起は多く見掛けますが、バイアスに関して触れているものは少数です。ご自身の検討において参考になれば幸いです。
・さらに上級の方(実際にクオンツ運用に従事されている方など)
クオンツ運用にはビッグデータ分析の波が押し寄せています。AIによるオルタナティブデータの活用事例は様々な箇所で見掛けるようになりました。しかし一方で、AIを使ったバイアス対策事例は殆ど見掛けません(内々に研究しているのかもしれませんが)。本記事が一石を投じることになればよいと考えています。
(2)お断り
このnoteに記載する内容は筆者独自の研究によるものです。本職の方で何か気付いた方がいればフィードバックを頂けると幸いです。
1.バイアスの罠
(1)本記事におけるバイアスの定義
本記事におけるバイアスとは、データ・スヌーピング・バイアスを指します。データ・スヌーピング・バイアスとは、「本来であれば全く有意性がないものを誤って有意性があると判断してしまう過ち」のことです。統計用語では、タイプIエラー、偽発見(False Discovery)、偽陽性などとも呼ばれます。過剰最適化(過学習、オーバーフィッティング)はここでいうバイアスには含めません。
(2)バイアスの簡単な事例
今、あなたは来たるべきチンチロの勝負のために、6の目が出やすいグラ賽を探しています。あなたはサイコロ業者から10000個のサイコロを取り寄せて、この中で6の目が出やすいものを選り分けようと考えました。そこで、各サイコロについて5回振って出た目を記録することにしました。

そうすると、10000個のサイコロの中で5回全て6の目が出たものが、ちょうど3個見つかりました。あなたはこの3個のサイコロを持って意気揚々とチンチロの勝負に出掛けました。さて、あなたは無事チンチロで勝利を収めることができるのでしょうか。
A:当然圧勝する
B:通常の運天賦の勝負にしかならない
この問題の答えは当然Bです。読者の方でAを選んだ方はいないでしょう。しかし、なぜかトレーディング戦略の構築過程ではAを選ぶ方が多いのです。
とにかく手当たり次第やってみると偶然良い結果が得られることがあります。これが本記事でいうバイアスです。逆に言うと、多数回試行することで比較的簡単に見せ掛けのパフォーマンスが良い戦略を得ることができます。このような粗悪な代物が商材として出回っている可能性(意図したものか意図していないものかは置いておいて)は否定できないのです。
(3)バイアス対策技術の必要性
トレーディング戦略の構築過程では、未知のアルファを探すために多数の戦略について検証を行う必要があります。これが前節の状況にそっくりそのまま当てはまることになります。
例えばEA構築では、有効な投資指標の選定やパラメータの最適化を行うことで膨大な数の試行が発生します。また昨今のクオンツ運用を例に取ると、AIを使って非構造化データ(テキストや画像、音声などコンピュータが直接扱うことが難しいもの。従来のデータに対してオルタナティブデータと呼ばれています)から投資指標を抽出し、しらみ潰しにアルファの発掘を行っています。
しかし、我々が行っていることは「あるかどうかも分からないグラ賽を探す行為」であることを再認識すべきです。検証で少しばかり良い結果が得られたとして、どうしてその結果が信用に値すると考えることができるのでしょうか。
このような検証作業に労力を掛けたとしても、肝心のバイアス対策技術を有していない限り、悲惨な結果が待ち受けています。大変な労力を使ってやっとのことで得た良好なパフォーマンスは人間の心理的に否定しがたく(一種のサンクコスト効果)、このため客観的でスクリーニング能力の高いバイアス対策技術がトレーディング戦略構築における要素技術として必要不可欠なのです。
2.バイアス対策の歴史
トレーディング戦略の評価にはシャープレシオやプロフィットファクターが使われることが多いのですが、統計的観点からは全く異なります。統計的観点によると、まず「バックテスト等で得られたリターンは、全く期待値のない母集団から抽出されたものである」という仮説を置き、この仮説が棄却できるかどうかを検証します。
本章では、バイアスに対するアプローチの歴史を紐解きます。
(1)統計的仮説検定
1933年、ネイマンとピアソンはある母集団から得られた標本を用いて仮説を検証する手順を考案しました。調査研究者は予め仮説を設定し、その仮説が正しいと仮定した上で観察された標本が得られる確率を求め、その確率が設定値よりも十分小さければその仮説を棄却する(対立した仮説を採用する)手法です。この検定の目的は、対立仮説をある程度の確度を持って正しいと結論付けることでしたが、誤った結論を導く確率を予め受け入れる(つまりバイアスの存在を認知し許容する)ことが大前提でした。
1936年、ボンフェローニは仮説検定を複数回適用すると誤った発見(以下偽発見)が起こる可能性が高くなることを指摘しました。ボンフェローニは検定をn回繰り返す場合は、設定する有意水準を1/n倍に厳しく設定する必要があることを提案します(ボンフェローニ補正)。しかし、ボンフェローニの提案は暫くの間無視されることになります。当時は手計算の時代であり、確率計算を多数回試行することは稀であったためです。
(2)多数回試行を考慮した指標の導出
1987年、HochbergとTamhaneは「Familywise Error Rate(以下FWER)」を考案しました[1]。これは多数回試行のうち、少なくとも1つの偽発見が発生する確率を示すもので、これを有意水準の代替として用いることを考えました。しかしこれは「たった1つ」の偽発見を減らそうという試みであり、試行回数の増加に応じて非常に厳しい閾値が必要となるため、現実的な解法にはなりえませんでした。
1995年、BenjaminiとHochbergは「False Discover Rate(以下FDR)」を考案しました[2]。これは試行回数に応じて間違いを許容するという考え方であり、FWERと同じく試行回数の増加に応じて閾値は厳しくなるものの、FWERよりも現実的な手法として受け入れられました(このあたりは参考文献[3]に分かりやすく解説が載っています)。
(3)ランダム化を使った検定
2000年、Whiteはブートストラップ法を有意性の評価に用いる手法を考案しました[4]。これがWhiteのリアリティチェック(以下WRC)と呼ばれる手法です。ブートストラップ法とは1979年にEfronが考案した手法であり、手元にある標本からランダムに復元抽出を繰り返すことで元々の母集団の分布を計算的に予測するものです。
2007年にはAronsonがWRCをトレーディングの検証結果の評価に適用する事例について書籍にて触れています[5]。
2006年、Mastersはトレーディングの検証結果の評価のためにMonte-carlo Permutation法(以下MCP)を考案しました[6]。トレーディング結果に対して復元抽出を繰り返すブートストラップ法に対して、MCPは元々のアセットのリターンを対象としたランダム化手法であり、対象のトレンドを除去した後、その順序と符号についてランダム化を行うことで予測力を持たないトレード戦略のバラツキの分布を得るものです(復元抽出はしない)。
(4)その他の手法
上記のほかにも2000年代に入ってから様々な手法が考案されています。
・Superior Predictive Ability Testing(SPA) Hansen(2005)
・Stepwise multiple testing(STEP-M) Romano, Wolf(2005)
・Extension of White's Reallity Check (EWRC) Corradi, Swanson(2011)
2018年にはPerumalとFlingがこれらの評価手法のどれが優れているのか、トレーディング戦略のルール選定に適用した場合の効果について論文を著しています[7]。
(5)トレーディングの最適化に特化した手法
2014年、WaltonはSystem Parameter Permutation法(以下SPP)を考案しました[8]。これはトレーディングの最適化過程において各々のパラメータにウィンドウを与え、得られるパフォーマンスの分布を参照することで真のパフォーマンスを推定するものです。単純に手持ちのデータを使って判断する(3)のランダム化手法に対して、このようにデータを追加したり自身で生成したりして多角的に判断する手法は非常に有効だと考えています。
3.AIを使った新しいバイアス対策
本章からはAI(すなわち機械学習)を使ったバイアス対策について説明します。
(1)セレベラム・キャピタルのシーブ
セレベラム・キャピタルはAI運用を行うヘッジファンドです(過去にブログで紹介しました)。セレベラムのAI運用の特徴は、とにかく多数の運用戦略を自動的に生成することです。生成された運用戦略はそのパフォーマンスに応じてリーダーボードにランク付けされ、リーダーボード上位の戦略を組み合わせて運用することになります。
しかしこれまでに問題提起してきたように、バイアスの影響によってリーダーボード上位の戦略を単純に選ぶだけでは実際に利益を出すものは全体の52%程度に留まるとのことです。
ここで、シーブ("ふるい"の意)と呼ばれるバイアス対策技術でスクリーニングすることによって、実運用で利益を出すものが75%まで大幅に改善されるようです。このシーブに関する資料がweb上に落ちています[9]。これを取り掛かりとして、機械学習によるバイアス対策技術とその展望について論じます。
(2)シーブのモデル
シーブのモデルは以下のグラフィカルモデルで表されます。

xはインサンプルデータによるリターン(言い換えるとバックテストの結果)、yはアウトオブサンプルデータによるリターン(言い換えるとフォワードテストや実運用の結果)です。Bはバイアス量、Fはアルファ(つまり真の収益能力)です。gは各戦略の自動生成プロセスにおけるパラメータ(フレームワークの与え方)、sは各戦略に使われるパラメータ(投資指標や閾値など)を示します。
xはアルファとバイアスの両方から影響を受けます。yはモデル構築には使われていないので、バイアスの影響は受けずアルファだけに依存するものと仮定します(実際にはアウトオブサンプルのデータに対してもバイアスは存在するが、xへの影響よりも小さいと考える)。
バイアスBはgとsから両方影響を受けます。これに対してアルファFはsのみから影響を受けます。gとsの区分が分かりづらいと思いますので少し説明します。例えばgはトレードの時間軸の選び方{1D, 4H, 1H}、sは移動平均の計算期間{7, 14, 21}等とお考え下さい。gの選び方は直接アルファを生成するものではありませんが、試行数が増えたりトレード対象の分散値が変わることからバイアスへは影響します。sの選び方はバイアスとアルファの両方へ影響することになります。
前章で紹介した従来の統計的手法とシーブの比較を以下に示します。どの手法もランダム化によって推定した母集団の確率分布からトレーディング戦略の妥当性を評価する手法となります。

さてシーブの目的は、トレーディング戦略が持つアルファFの事後分布(g、s、x、yが観測されたときのアルファFの分布)を求めることです。この事後分布は以下の式で表されます。
![]()
この式は条件付き確率の式であるため、以下の同時分布に比例します。
![]()
一方、上図のグラフィカルモデルを確率式で記述すると、
![]()
上式を確率の乗法定理を用いて変換すると、
![]()
この式から観測されないバイアスBを周辺化を用いて除去します。
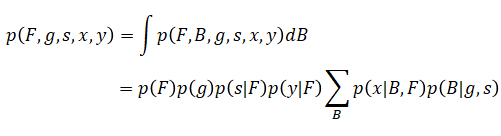
以上をまとめると、目的であるアルファの事後分布は以下のように表すことができます。
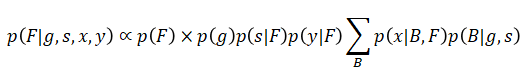
(3)AIによるトレーディング戦略の評価指標とその展望
前節で導出したアルファの事後確率(g、s、x、yが観測されたときのアルファの確率)の右辺は、アルファの事前確率p(F)とアルファの尤度(残り全ての項)の積で表されています。この形であればMCMC(マルコフ連鎖モンテカルロ)を用いてアルファの事後分布に従うサンプルをランダム生成することができます。ただし尤度の式はバイアスに関する周辺化(積分)を含んでおり、解析的に定式化することができません。このため尤度を計算する際には数値積分を使う必要があり、計算過程もかなり煩雑なものになります。
一方、シーブのモデルはグラフィカルモデルであることには変わりはないので、ベイジアンネットワークを使って予めDAG(有効非巡回グラフ)構造を指定しておいて、潜在変数であるアルファとバイアスをNA値とおいて推定させる方法も考えられます。
これらの所作から得られたアルファの確率分布を用いて、様々なトレーディング戦略の評価指標を考えることができます。得られたアルファの確率分布について単純に期待値やスキューネスを指標とすることもできますし、アルファのP値を計算することもできます。またアルファとバイアスが個別に推定されているのですから、アルファだけで判断するのではなくアルファとバイアスの比を使ってSN比のような考え方でスクリーニングする方法も面白いかもしれません。
アルファを無理に推定しなくとも、グラフィカルモデルではアルファとアウトオブサンプルリターンが密接に結びついているため、アウトオブサンプルリターンの確率分布を考えるだけでも評価の確度は高くなる可能性があります(SPPに近い考え方になります)。またこのモデルのようにアルファを固有の潜在変数とするのではなく、アウトオブサンプルの確率分布の平均値パラメータと考えてその確率分布を推定するやり方もあると思います。
また、シーブのモデルにはアセットのリターン特性が考慮されていません。アセットの持つ特性(分散やスキューネス)も戦略のパフォーマンスに大きく影響します。これらをモデルに取り込むことも考えられる手法の1つです。
(4)スクリーニング能力の確認結果
ここでは実際にシーブを構築し、従来のP値による変数選択とシーブを使った変数選択の両者について、統計的エラーの発生頻度をモンテカルロシミュレーションにて比較しました。
<シミュレーション条件>
以下の条件にて乱数を使って目的変数と説明変数を生成してエラーの発生頻度を確認します。
・各戦略のリターンサンプル数=1000
・説明変数の予測能力(情報係数)={0.0、0.1}の2値
(有意でない変数と有意な変数)
・モンテカルロ繰り返し数=1000
・評価指標はアルファの下側確率(0以下となる確率)とした
(本指標が小さいほうが有意であり正のアルファが存在する)
<グラフィカルモデル>
Rにて作成しています。今回はフレームワークは固定であるため、変数gは取り入れていません。

<検証結果>
各変数の確率分布はモンテカルロ1000回試行のうちの1つ(代表値)です。また、統計的エラーの発生頻度について、タイプIエラー評価時はタイプIIエラーの発生率を5%水準に固定、タイプIIエラー評価時はタイプIエラーの発生率を5%水準に固定しています。


上記のように、トレーディング戦略の評価にバイアス対策となるAI(機械学習)を用いることで、エラーの発生頻度を大きく低減できることを確認することができました(ただし上記はあくまでも情報係数や分散などが時系列で一定である理想状態であることに注意して下さい)。
4.結論
さて、実際には多額の運用資金が掛かっていない限り、ここまで厳密にバイアス対策を行う必要はありません。ここで特に初学者の人に知っていただきたいのは、このような研究を持ってしてもバイアスを完全に防ぐことは不可能であり、ましてや完全に儲かる自動売買を与えられた情報だけで見抜くことは不可能だということです。世の中に美味い話はないのです。甘い謳い文句に誘われて自動売買商材の養分になることがないよう注意してください。
本記事では、トレーディング戦略構築におけるバイアス対策技術の必要性を説き、バイアスに対するアプローチの歴史と機械学習を使った新しいバイアス対策技術の可能性について論じました。本記事で紹介した機械学習手法は比較的単純なグラフィカルモデルをベースとしており、これを取り掛かりとして様々な手法へ発展できる可能性があります。
機械学習によるバイアス対策技術(統計的エラーの低減技術)は、今後AI投資が活発になる中で要素技術となる可能性が高く、非常に研究余地の大きい分野だと考えています。私も微量ながらAI投資分野の発展に力添えしていけたら幸いです。
5.参考文献
[1]"Multiple Comparison Procedures" Hochberg, Tamhane, 1987
[2]"Controlling the False Discovery Rate : A practical and Powerful Approach to Multiple Testing" Benjamini, Hochberg, 1995
[3]"P値とQ値" 梅田, 2018
[4]"A Reality Check for Data Snooping" White, 2000
[5]"Evidence-Based Technical Analysis" Aronson, 2007
[6]"Monte-Carlo Evaluation of Trading Systems" Masters, 2006
[7]"Systematic Testing of Systematic Trading Strategies" Perumal, Flint, 2018
[8]"Turning Data Mining from Bias to Benefit through System Parameter Permutation" Walton, 2014
[9]"Meta-Machine Learning : Automatic Programming of Trading Strategies" Andre, 2017
