
トレーディングの統計モデリング
0.はじめに
(1)トレーディングスタイルと統計モデリング
トレーディングのスタイルには様々な定義があります。その中でも定性的な判断に基づくジャッジメンタル運用(いわゆる裁量)と、定量的な判断に基づくクオンツ運用(システムトレーディングもこれに含みます)は、とても対照的なスタイルだと思います。
クオンツ運用ではモデルに基づいたトレーディングを行います。これには様々なモデルが存在しますが、本noteの題材である統計モデルとは、現実の事象を既知の確率分布(正規分布やポアソン分布など)に当てはめてパラメータを同定したものです。そしてこの統計モデルを使って現実の事象を分析したり、超過リターンやそのばらつきを予測するのです。
(2)本noteの着地点
本noteでは実際にトレーディングに使う統計モデルを作るのではなく、統計モデリングの考え方と金融商品のデータの特性(というよりも素性)を照合することでその予測の難しさを説き、実運用における勘所について触れることです。そして読者各位のトレーディングスタイルに対して何らかのインスピレーションを与えることができれば幸いだと考えています。
(3)お断り
トレーディングのモデルは、例えばアクティブ運用理論や計量時系列分析などがありますが、実際の金融商品に対してどのように統計モデルを適用すべきか論じたものは見掛けません。このnoteに記載する内容は筆者がこれまで独自に研究を重ねてきたものであり、簡便に説明するために一般書籍と異なったアプローチの仕方で説明します。
統計専門の方で何か気付いた方がいれば、ご指摘いただけると幸いです。
(4)参考書籍
「データ解析のための統計モデリング入門」-久保拓弥、2012年5月18日
1.一般線形理論における”過分散”
(1)トレーディングにおける予測とは
トレーディングにおける予測の目的とは、とどのつまり利益を得るためのものであり、現時点における既知の情報を用いて未来の事象の予測を試みるものです。ですが、そもそも未来の予測なんてできないということを頭に入れておくべきです。従って、我々がすべきことは、未来の値動きを予測する式を立てると言うよりも、事象の因果関係を明確にすることでその結果わずかながらにおこぼれを頂戴する、という言い方がより適切であると考えています。そしてこの因果関係が「より強く」「より知られていない」ほうが貰えるおこぼれの量が増える傾向にあります。
(2)一般線形理論
最も簡単なモデルは下記に示す線形回帰モデル(シングルファクターモデル)です。一般的にトレーディングにおけるシングルファクターモデルとは、タイムシリーズのものとクロスセクションのものに分類されます。
(a)タイムシリーズモデル
下記の式は時刻tにおけるファクターftについて、それと同期間のリターンrtの関係を示す式です。この式自体は未来を予測するものではなく、特定の期間における事象の関係(因果関係ではなく相関関係)を説明するものだと解釈できるでしょう。aは固定値でありトレンド項(ドリフト項)を示します。ここでラグを設けると途端に説明力が落ちてしまいます。なぜなら物事の説明力には必ず減衰期間(半減期)が存在し、インターネットなどの情報が発達した現代ではその半減期は非常に短いものであるからです。εtは各tにおける残差項です。
![]()
(b)クロスセクションモデル
クロスセクションモデルとは、その名のとおり「横断的」にファクターとの関係を表すモデルです。多数の個別銘柄が集まる株式市場を想像すると分かりやすいと思います。説明対象である個別銘柄の集まり全体をユニバースと呼びます。ここでriは銘柄iのリターン、uiはファクターに依らない個別な収益部分でありスペシフィックリターンと呼びます。xiは銘柄iのファクター値であり、ファクターエクスポージャーと呼びます。bはそのファクターによるユニバース全体の説明力を示し、ファクターリターンと呼びます。εiは各銘柄における残差項です。
![]()
以降、比較的理解しやすいタイムシリーズモデルについて、実際の金融商品のデータやシミュレーションの結果を見ながら解説していきます。
(3)観測されない個別の外乱
シングルファクターモデルは現実の事象をたった1つのファクターで説明しようとする試みです。当然、1つのファクターだけでは説明できる範囲に限りがあるでしょう。それならば可能な限りファクターを増やしてみてはどうでしょうか?
![]()
上記は、観測したファクターを可能な限り取り入れたマルチファクターモデルです。マルチファクターモデルは多重共線性や過剰最適化の問題があって実際の適用は難しいのですが、ここでは上手くモデリングができたとします。それでもなお、観測されない個別の外乱が存在します。この個別の外乱の影響が非常に大きく、モデリング上の問題となるのです。
(4)外乱の影響を定量的に把握する
ここでは問題を単純化して考えます。ある単一のファクターが観測した情報を全て含んでいるものと仮定します。このとき、モデルをそのファクターによる真のモデルの部分と外乱の部分に分けて考えます。

ここで外乱項dtは、平均0、分散sdの正規分布に従うものとします。この外乱は全く観測されない個別要因によるものなので、他の変数との共分散は0です。この外乱とは例えば、天気、要人発言、災害等と考えてください。すなわちモデルに取り入れることができなかった全ての事象です。
この外乱項の分散sdの多寡による影響をモンテカルロシミュレーションで観察していきます。
(a)検定による統計的エラー
下図は外乱項の分散sdを変化させたときの、タイプIIエラー(本来は有効である指標を見過ごしてしまうエラー)の発生頻度です。有意水準の設定や真のモデルの説明力によって傾向が変わりますが、外乱項の分散が大きい場合はこのエラーの発生頻度が著しく上昇することが分かります。

(b)バランスカーブのバラツキ
下図は外乱項の分散sdを変化させたときの、バランスカーブのバラツキを示します。さらにその下には取引回数2000回×200試行のシミュレーション結果における、総損益の期待値(平均)、総損益のバラツキ(標準偏差)、総損益のシャープレシオを示します。期待値は外乱に依らず一定ですが、シャープレシオは外乱項の分散とともに悪化することが分かります。


(5)過分散の影響と統計モデリングの目的
結論として、外乱項の分散が大きい場合は統計的エラーの発生頻度が上昇し、それと同時に実運用のパフォーマンスが悪化します。すなわち、トレーディングに有効な指標の選定が難しくなり、仮に有効な指標を選定できたとしても運用成績のバラツキからその継続が難しくなります。
真のモデルの分散に対して相対的に外乱項の分散が大きいことを過分散と勝手に呼んでいます(学術的な過分散の定義は別にあり、それは次章にて説明します)。統計モデルを作る上で致命的な影響を受けることになります。
過分散は統計的エラーの発生頻度を増加させます。「この指標は効くだろう」とせっかく目を付けた指標が、外乱の影響で有意とみなされず見過ごされてしまうのです。これは真のモデル部分すなわちトレーディングスキルの向上を著しく阻害します。
またバランスカーブのバラツキを見ても分かるように、真のモデル部分すなわちトレーディングスキルによる期待収益は外乱に依らず一定です。にも関わらず外乱の大きさで損益がバラつくということは、過分散の場合にはトレードの大部分が運要素で決まることを示しています。より外乱の大きいアセットでは、トレーディングスキルを有していても収益がマイナス転落することも多く、その反面偶然によるスーパースターが生まれやすくもなります。過分散をどうにかしてケアすることで自身のトレーディングスキルを向上させるとともに少しでも運ゲーから脱出することが統計モデリングの目的のだと考えています。
2.”過分散”について-さらに一歩進んだ学術的説明
これ以降は参考書籍に基づき実際の金融商品の特性と照合しながら解説を行います。
(1)現実のデータの扱い方
前章で紹介した一般線形理論では現実のデータ分析に対応できません。前章で考えた真のモデルは単純な正規分布を仮定しています。実際のデータ、特に金融商品のデータは正規分布やポアソン分布などの既知の分布では適合しないようなバラツキを備えているからです。
この問題に対しては様々なアプローチが存在します。例えば、金融商品のファットテールな分布に対応するために正規分布ではなく一般化双曲型分布を適用する、マルコフ転換モデル(レジームスイッチ)を用いて市場のボラティリティに起因する分布の変化に対応する、異常値(アウトライヤー)を表現するために時系列のジャンプ拡散過程を導入する、などが挙げられます。
参考書籍7章に記載のあるGLMM(一般化線形混合モデル)では、前章で説明した外乱を「人間が測定できない・測定しなかった個体差」としてモデルに組み込み、この個体差が過分散をもたらす要因としてモデリングを進めていきます(以下、外乱は個体差と読み替えます)。
ここではまず、統計モデルにおける過分散について学術的な定義を説明します。個体差のケアの方法は次章で説明します。本章は読み飛ばして頂いて構いません。
(2)単純なモデルにおける”過分散”
ここで言う単純なモデルとは、二項分布やポアソン分布など1つのパラメータが決まれば自動的に分散が決まるモデルを指します。このとき、実際のデータが既知の分布で想定されているよりも大きな分散を持っていることを過分散と呼びます。
ここでは日経平均株価およびビットコイン価格の価格レンジ(日次)を例に挙げて、それぞれが過分散かどうか確認してみましょう。
<ポアソン分布を仮定する場合>
ポアソン分布はそもそも離散する事象をカウントする確率分布なのでこれを日々の価格レンジに適用してよいかどうかという議論はあります。が、とりあえずここでは何も考えずに当てはめてみます。ポアソン分布はただ一つのパラメータλを持ち、分布の平均=λ、分布の分散=λという、平均と分散が等しいモデルです。
以下の結果を見ると、日経平均の価格レンジの分散は最尤推定したポアソン分布で想定される分散よりも小さくなっています。しかしビットコインの価格レンジは分散は最尤推定したポアソン分布で想定される分散よりも遥かに大きな値であり、ポアソン分布に当てはめた場合ビットコインの値動きは過分散であると言えます。

(3)複雑なモデルにおける”過分散”
ここで言う複雑なモデルとは、正規分布やガンマ分布など複数のパラメータを持つ確率分布を指します。正規分布やガンマ分布は確率分布のパラメータを2つ持ち、そのため平均と分散を独立に決めることができます。ここでは先程と同じく日経平均株価およびビットコイン価格の価格レンジ(日次)を複雑なモデルに当てはめてみます。
<ガンマ分布を仮定する場合>
ガンマ分布は連続確率分布であり、形状母数kおよび尺度母数θの2つのパラメータで特徴づけられます。分布の平均=kθ、分布の分散=kθ^2となります。ガンマ分布は指数分布やカイ二乗分布を一般形として拡張した分布であり、よく使われる連続確率分布と言えるでしょう。
以下の結果を見ると、日経平均とビットコインの両者の価格レンジは単純なモデルであるポアソン分布よりも良くフィットしていることが分かります。

このような複雑なモデルの過分散の度合いを考えるために、残差逸脱度という指標があります(詳細は参考書籍第4章を参照)。
逸脱度とは、モデルの当てはまりの悪さを表す指標であり、最大対数尤度log(L)を用いてD=-2log(L)で表されます。残差逸脱度とは、当てはめたモデルの逸脱度とフルモデルの逸脱度の差分です。フルモデルとはサンプル数と同じだけのパラメータ数を持ち、極限までデータにフィッティングさせたモデルです。当然ですが、当てはめたモデルの逸脱度>フルモデルの逸脱度となります。この残差逸脱度が自由度よりも大きい場合、過分散と定義します。データのサンプル数は様々であるため、当てはめたモデルの精度だけを単純に見るのではなく、完全にフィッティングさせたときの精度をベース分として差っ引いてモデルの適合度を判断する、というわけです。
(4)過分散への対応方針
ここまで長々と説明してきましたが、学術的な過分散に関しては詳細を理解する必要はありません。そもそもの問題は、現実のデータには個体差がありそれを考慮したモデルを作ることが重要である、ということです。つまり問題の本質は、学術的に定義される分布からの逸脱を示す過分散にあるのではなく、その原因となる前章で定義した個体差のバラツキの大きさを示す過分散についてどうケアするか、ということにあります。次章ではGLMMにおける個体差のモデリングと、個体差を考慮した分布の推定方法について説明します。
3.”過分散”とどう向き合うか
(1)個体差をモデル化する
個体差は決して観測されないため、データとしてモデルに取り込むことはできません。しかし、よく分からないけど何か個体差が存在する、ということは確率変数を使うことでモデル化できます。
結局、本noteの1章のように個体差riを以下のようにモデルに追加します。ここで個体差riは、平均0、分散sの正規分布に従うものとし、他の変数との共分散は0です。前半部分を固定効果、後半部分をランダム効果(変量効果)と呼びます。
![]()
個体差riは正規分布に従うため、特殊な個体(riが中心から逸脱している個体)の数は当然少なく、平均的な個体(riが中心近い個体)の数は多くなります。
個体差はグループとして影響を受けている可能性もあり、これを場所差と呼びます。場所差を考慮したり、個体差に正規分布以外の分布を仮定する場合はさらに複雑なモデルが必要になります。
(2)個体差を推定する?
これまでに散々問題提起してきた個体差ですが、これを何とか推定したいのです。しかし結論から言うと、そもそも観測されてない個体差なんてものはどう頑張っても推定できないのです。ではどうするか?これを補うための魔法のような方法があります。それが積分です。
以下、最尤推定のプロセスを説明します。そもそも最尤推定とは、尤度(当てはまりの良さ)を最大にする確率分布のパラメータ(ここではβ1とβ2です)を推定することです。尤度L(β1、β2)とは各サンプルがそのパラメータβ1、β2になりそうな確率を合算したもので、以下のように表します。この尤度が最大となるようなβ1、β2の値を求めます。求め方は数式を解いて定式化しても良いですが、一般的には数値解法で求めます。

ここで、個体差riが存在する場合を考えます。各サンプルのパラメータがβ1、β2で且つ個体差がriとなる確率は以下の通り、riがその値を取る確率で重み付けしたものとなります。

現実として、riの値は-∞から+∞の値を取りうるため、サンプルiのパラメータがβ1、β2となる確率は上式をriについて積分して求めます。確率分布の積分は必ず1となるため、最尤推定の式から個体差riの影響を除去することができます。

(3)この式の意味するところ
上記の式の意味するところは、各サンプルについて観測できる条件を固定してできるかぎり多くのデータを集め、その平均を取ることで推定の精度を上げようとする試みです。ここで集めるデータには個体差があっても構いません。これはつまり、無作為割り当てを行う調査観察研究と同じことです。
上記の式は、個体差riが正規分布に従う場合は比較的単純ですが、場所差を考慮するなどランダム効果の発生源が増える場合はそれに伴って多重積分が必要になります。この多重積分を効率的に解く数値解法の1つがMCMC(マルコフ連鎖モンテカルロ法)であり、マルコフ連鎖の性質上、ベイズ的に事前分布・事後分布が得られるため、MCMCを使う場合はベイズ統計モデリングと呼ばれます(少し乱暴な説明です。詳細については参考書籍を参照ください)。
(4)過分散と向き合う-指標選定編(=トレーディングスキル向上)
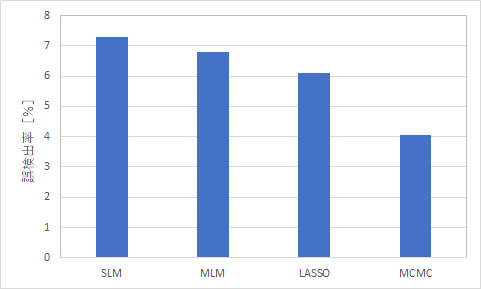
さて、ではMCMCを使った個体差を考慮した最尤推定は、単純な線形回帰と比較してどのくらい指標の選定能力が向上するのでしょうか。ここではサンプル数2000、説明変数200個のデータセットを1000セット用意し、各手法を用いて変数選択したシミュレーション結果を示します。
結果として、MCMCを使った最尤推定は一般線形回帰の有意水準による変数選択よりも本来有意でない指標の誤検出率を低減できることを確認しています。この結果はあくまでもシミュレーション上のものであり、現実のデータセットの場合は更なる効果を発揮するかもしれません。
(5)過分散と向き合う-運用編(=運ゲーからの脱出)
お気づきの方がいるかもしれませんが、この個体差を持つモデルの最尤推定の考え方は、クロスセクションでのファクターベットが有効である理由にそのまま当てはまります。あるファクター周りにとにかく銘柄を組み合わせれば、期待値はそのままで個体差の影響を低減することができます。これが現時点で8000万超を稼いでいる私たちの株式運用モデルの基幹となる原理です。

4.結論
ここまでをまとめます。
・金融商品のデータは殆どの場合で過分散であり、トレーディングスキルの向上が難しく運ゲーになりがちである。
・統計モデリングを行うことで、投資指標の選択における誤検出率を低減でき、トレーディングスキルの向上に寄与できる可能性がある。
・実際の運用では統計モデリングの考えに基づき、個体差の影響を軽減できるファクターベットを行うことで運用成績の安定につながる。
最後に断言しますが、トレーディングにおいて統計モデリングなど必要ありません。本noteでは、あくまでも統計モデリングの考え方に基づき、実際のトレーディングが非常に難しい問題であることを述べただけです。
重要なことは金融商品の素性を理解し、確率的な考え方を自身のトレーディングスタイルへ織り込んでいくことだと思います。
小難しい内容に最後までお付き合いいただき、ありがとうございました。
