航空大学校 総合Ⅰ予想問題
航空大学校一次試験の総合Ⅰ予想問題です。
図形問題はちらほら中学受験問題から取ってきたりして、若干難しめな気もします。
様々な無料のサイトから問題を拝借させていただきました。各サイトへのリンクは、解答&解説パートに埋め込んであります。ぜひ参考にしてください!
それでは50問、いってみましょう🔥
問題数:50問 制限時間:50分(受験番号マーク、名前記入時間を含む)
【1】東京(東経135度)が4月27日午前10時のとき、ニューヨーク(西経75度)は何月何日何時か。
①4月26日午後8時 ②4月27日午後8時 ③4月28日午前0時 ④4月26日午前8時
【2】10進数の16は、2進数で表すと何か。
①10001 ②11001 ③1000 ④10000
【3】ある青果店では、リンゴを4個、ミカンを5個買うと890円である。また、リンゴを7個、ミカンを3個買うと1040円である。このとき、リンゴを5個、ミカンを4個買うといくらかかるか。
①1070円 ②910円 ③860円 ④1000円
【4】ある便では、機長が1人、副操縦士が1人、客室乗務員が4人の計6人で運航する。6人の平均年齢は40歳である。副操縦士の年齢は48歳であり、客室乗務員4人の平均年齢は33歳である。
このとき、機長の年齢はいくつか。
①52歳 ②58歳 ③60歳 ④64歳
【5】箱の中に、赤玉が3個、黄玉が2個、青玉が1個入っている。
箱の中から玉を1個取り出し、色を確認した後、箱に戻す。これを3回繰り返す。
3回目に2個目の青玉を取り出す確率はいくらか。
①1/6 ②1/36 ③1/108 ④5/108
【6】野球チームの優勝決定戦がある。チームAとチームBが対戦し、先に4勝した方が優勝となる。一戦ごとの引き分けはなく、必ずどちらかの勝敗を決める。いままでにチームAは3勝1敗である。ここから決着がつくまでのパターンは、いくつあるかを求めよ。
①2通り ②3通り ③4通り ④5通り
【7】ある商品を分割払いで購入したい。購入時に頭金として購入価格の25%を支払う。次の支払いからは、購入価格から頭金を引いた残額を11回均等払いで支払う。その際は、購入時の残額の10%の利子が付き、それを残額に加えた額を11等分して支払う。
分割払いの1回分の支払額は、購入金額のどれだけにあたるか。
①1/20 ②3/40 ③11/40 ④1/11
【8】袋の中に赤球が4個,白球が6個入っている。これから同時に3個取り出すとき,取り出す赤球の個数の期待値を求めよ。
①1/2 ②3/2 ③5/6 ④6/5
【9】ある地点での飽和水蒸気量曲線は以下のグラフのようになる。
気温30℃、6.8gの水蒸気を含む空気1m3の露点は何度か。

①5℃ ②10℃ ③15℃ ④20℃
【10】空欄に入る図形としてふさわしい物を選べ。

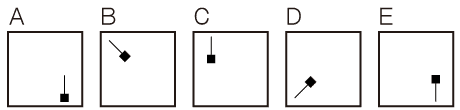
①A ②B ③C ④D ⑤E
【11】法則性
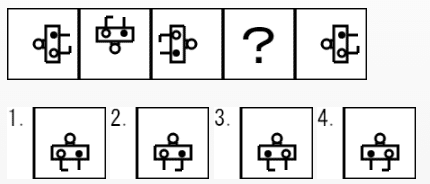
①1 ②2 ③3 ④4
【12】
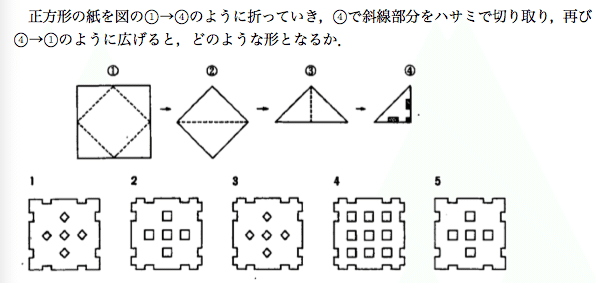
①1 ②2 ③3 ④4 ⑤5
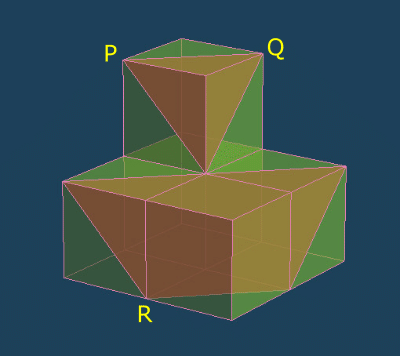
【13】PQRを通るように立体を切断したときの断面は、どのようになるか。
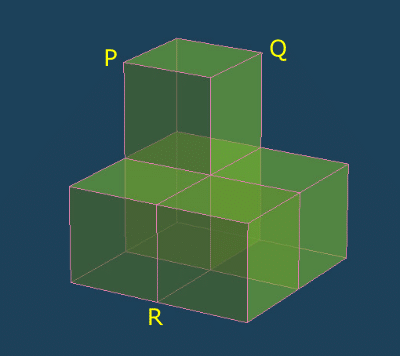
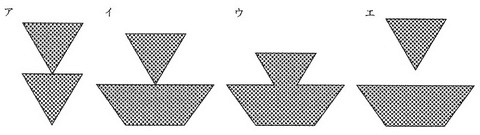
①ア ②イ ③ウ ④エ
【14】
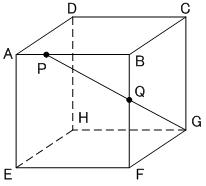
上の図は1辺が5cmの立方体で、辺AB上にAPの長さが1cm となる点P を、辺BF上に点Qをとる。PQ+QG が最も小さくなるとき、BQの長さは何cmか。
①20/7 cm ②25/7 cm ③20/9 cm ④22/9 cm
【15】同じ大きさの立方体の積み木をいくつか使って積み上げました。真正面から見た図、真横(右)から見た図、真上から見た図は次のようになった。立方体の積み木は、何個使ったか。
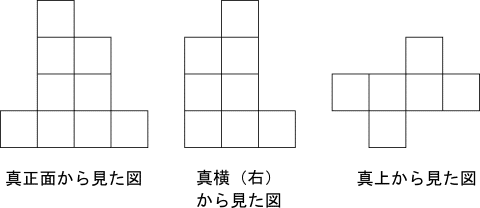
①13 ②15 ③18 ④21
【16】この展開図を組み立てたとき、図の頂点アと重なるのはどの頂点か。
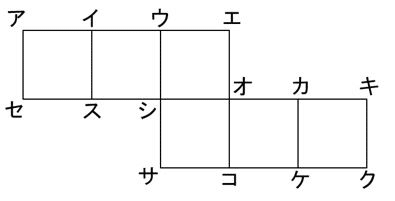
①ク ②ケ ③カ ④キ
【17】A~Dの選択肢の中で、問題に示した見本の図形を回転させた図形はどれか。

①A ②B ③C ④D
【18】100個の直方体があり下のように積み重ねた。黒丸の部分を突き刺し反対側まで貫通させる場合、貫通した直方体の数を求めよ。
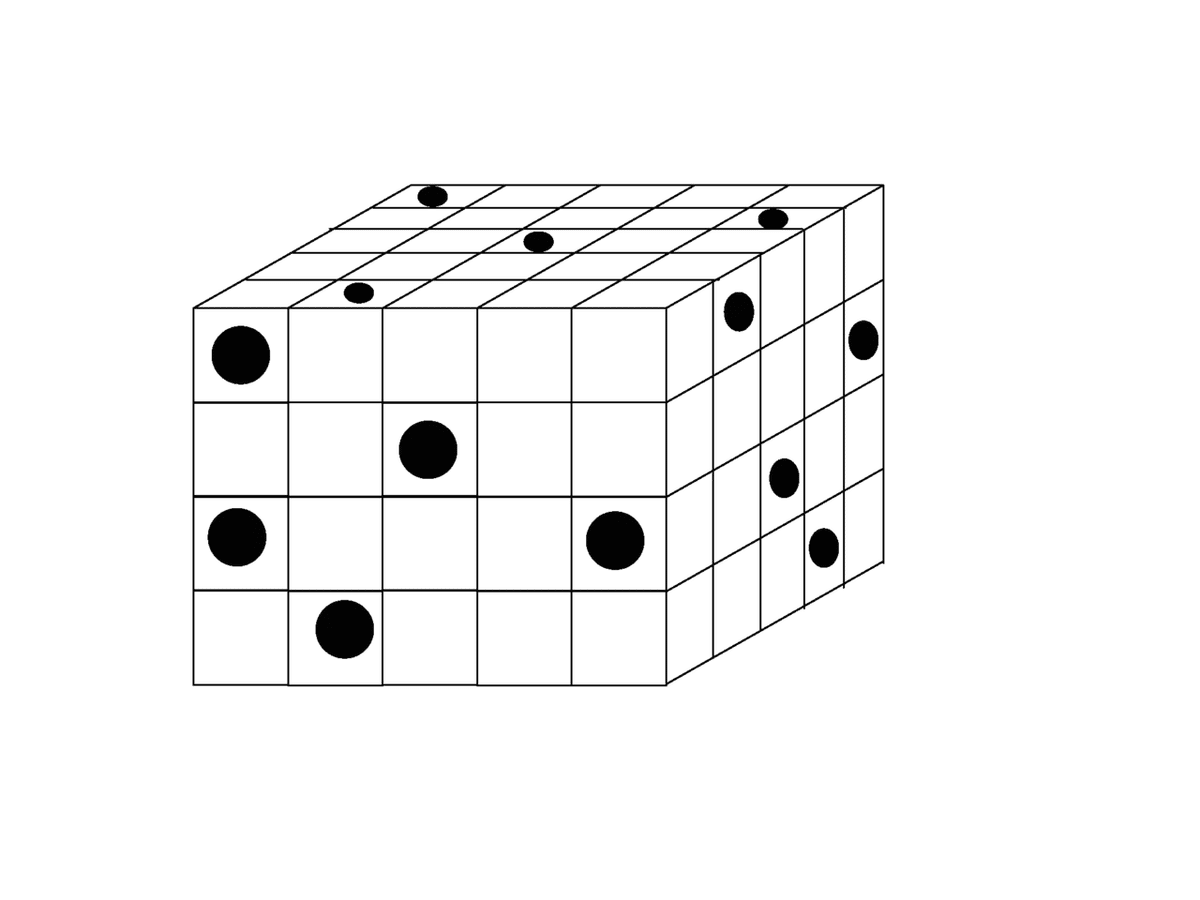
①52個 ②46個 ③50個 ④48個
【19】数列 2,4,8,14・・・がある。この数列の第7項は何か。
①46 ②56 ③112 ④44
【20】数列5,16,27・・・がある。この数列の第14項までの和は何か。
①1071 ②1088 ③1001 ④1064
【21】11+12+・・・・+18+19+20の値は何か。
①135 ②155 ③160 ④175
【22】縦、横、斜めの数字の和はそれぞれ等しくなる。アに入る数字は何か。
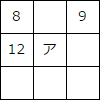
①10 ②11 ③12 ④13
【23】数直線上で、点Pが原点Oから出発して、正の向きに1だけ進み、次に負の向きに1/2だけ進む。さらに、正の向きに1/4だけ進み、次に負の向きに1/8だけ進む。以下。このような運動を限りなく続けるとき、点Pが近づいていく点の座標は何か。
①1/3 ②2/5 ③2/3 ④1/4
【24】図1の形をしたブロックがある。これを3つ組み合わせて図形を作る。(ア)~(カ)のうち、図1のブロックを3つ組み合わせてできる図形は何個あるか。
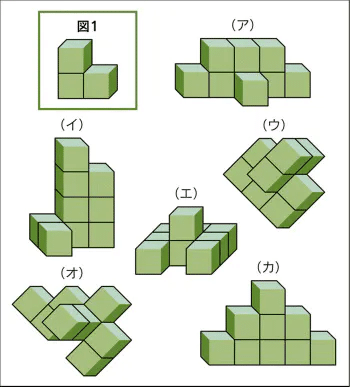
①1 ②2 ③3 ④4
【25】週末に読書をした。金曜日に全体の4/15を読んだ。土曜日は、残ったうちの2/9を読んだ。日曜日には、73ページを読んで81ページ残った。残りのページは、全体の何割か。
①1.5割 ②3割 ③3.6割 ④4割
【26】Aは2.7㎞/時で、Bは3.6㎞/時で歩く。AがX地点からY地点まで歩いて、42分かかる。
いま、AがX地点からY地点の向かって、BがY地点からX地点に向かって同時に歩き始めた。何分後に二人は出会うか。
①12分 ②14分 ③18分 ④20分
【27】次のカ、キ、ク、の3つの式によって表される領域はどれか。
カ:y < -x² + 8
キ:y < -2x + 8
ク:y >0

①1 ②2 ③3 ④4
【28】
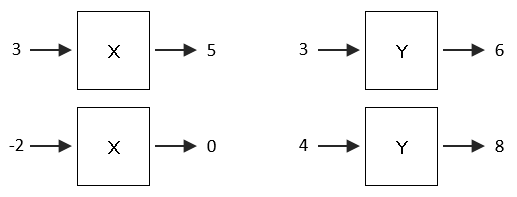
次のようにブラックボックスをつないだ装置がある。
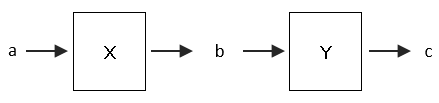
cが78の場合、aの値はいくらになるか。
①30 ②37 ③39 ④42
【29】以下の割引がある美術館で、小学生1名と中学生1名、大学生1名が一緒に入館する場合、総額はいくらになるか。(入館料=a円)

●小学生以下は子供料金(0.5a円)。
●学生割引は中学、高校生が対象。
●回数券は、複数人での使用も可。ただし、残余券払い戻しは不可。
●夫婦50割り引きは、同伴の男女どちらかが50歳以上なら2名に適用。
●団体割引は5人以上で利用の場合、全員に適用。
●各割引は他の割引と併用不可。
①2.1a ②2.3a ③2.4a ④3a
【30】以下の料金体系となっているホテルに、8月24日(金)8月25日(土)、8月26日(日)の合計3泊、宿泊する。ただし、1,2泊目は本館に、3泊目は新館に宿泊する。
大人1人、子供2人で宿泊するとき、代金はいくらか。

①50,000円 ②52,000円 ③54,000円 ④58,000円
【31】次のグラフより、人口が1500万人以上の地域はいくつあるか。
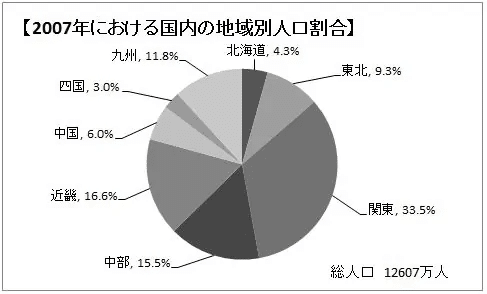
①1つ ②2つ ③3つ ④4つ
【32】次の都市群で、人口密度が3番目に大きい都市はどれか。
都市 面積[km^2] 人口[万人]
イヌ 35000 124500
ネコ 750 78900
トラ 26700 56800
ライオン 1000 19000
①イヌ ②ネコ ③トラ ④ライオン
【33】下表は、P県の耕地面積と、その使用内訳を割合を表したものである。P県の果樹地の耕地面積が9800haのとき、P県の田の耕地面積の割合は何%になるか
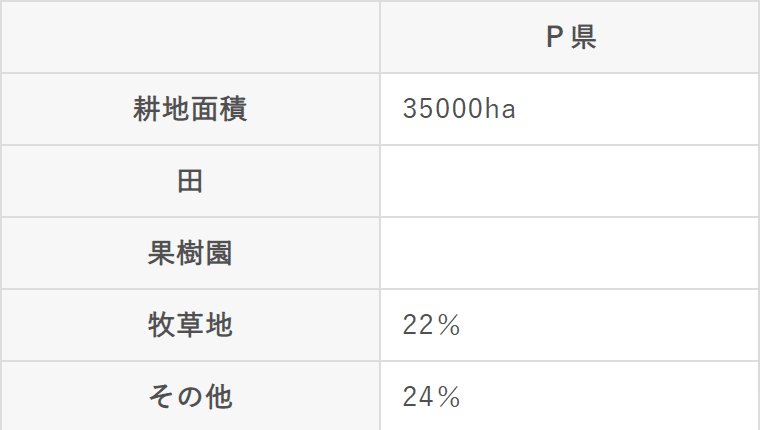
①25% ②26% ③28% ④32%
【34】

【35】ある規則で並んだ数字。次のうち、「?」に当てはまるのは何か。
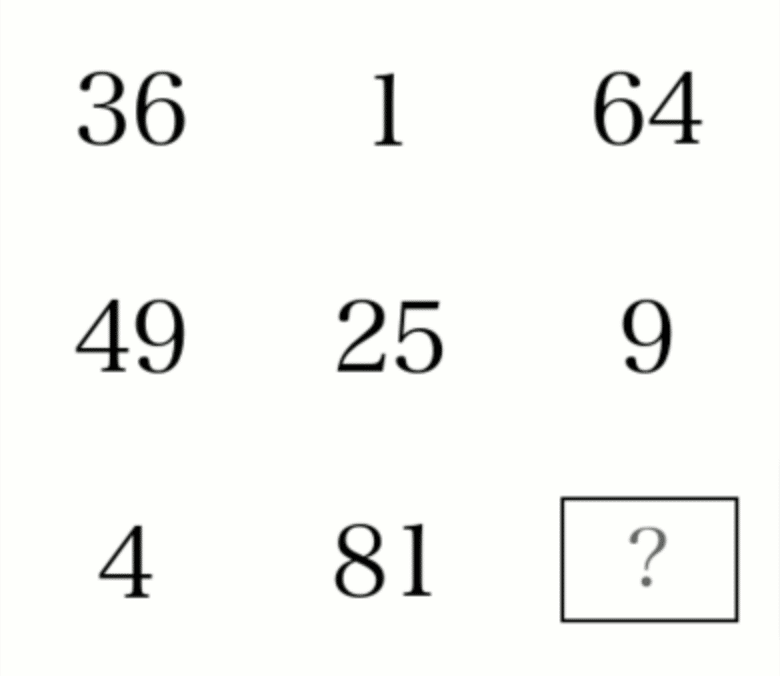
①128 ②53 ③27 ④16
【36】試験の採点業務を20日間の採点期間で終わらせなければならない。10日間、15人で採点をしたところ全体の1/3進んだ。残りの日数で予定通り終わらせるためには、何人増員すればよいか? ただし参加人数の1日あたりの仕事量は同じとする。
①12人 ②15人 ③18人 ④24人
【37】24% の食塩水 250g と 16% の食塩水 750g を混ぜると、何 % の食塩水ができるか。
①18% ②26% ③12% ④20%
【38】
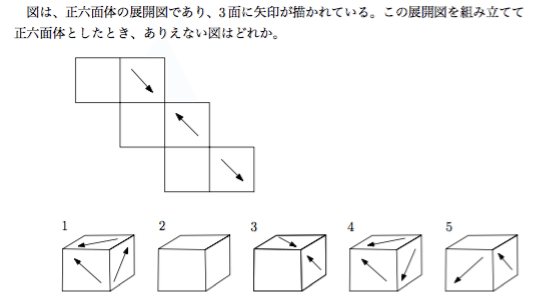
①1 ②2 ③3 ④4 ⑤5
【39】静水時では時速 10km の船が、流速が時速 2km の川を 3 時間上った。船の進んだ距離を求めよ。
①20km ②22km ③24km ④30km
【40】密度と太さが一様な1mの棒の一端に、2kgの物体Aを吊し、棒を支える支点を様々な位置に移動する実験を行った。支点の位置を、物体Aを吊した側から0.4mの位置にしたところ、釣り合って棒が水平になったという。棒の質量を求めよ。ただし、重力加速度はgm/s^2とする。
①6kg ②7kg ③8kg ④9kg
【41】20Ωの抵抗と、起電力9Vで内部抵抗1Ωの電池を接続した。このとき回路を流れる電流は何Aか求めよ。
①0.33A ②0.43A ③0.45A ④0.5A
【42】傾角30°のなめらかな斜面上に、2.0kgの物体をのせた。この物体を斜面上に静止させたいならば、何Nの力を加えればよいか。
①19.6N ②4.9N ③12.4N ④9.8N
【43】10000mm^2の面積に3kNの力がかかっている。
このとき、圧力は何MPaか
①0.3MPa ②0.6MPa ③1.2MPa ④1.6MPa
【44】抵抗Rと電圧計Vの値の組として正しいのはどれか。
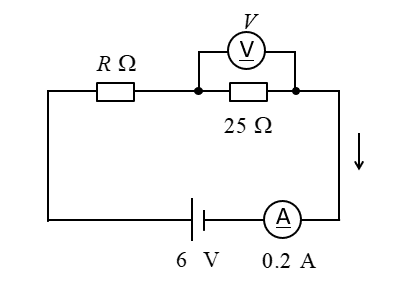
①R:3Ω、V:7V ②R:5Ω、V:10V ③R:5Ω、V:5V ④R:7Ω、V:5V
【45】ある速さで進む質量1.0kgの物体に、72Jの仕事をすると、その速さが20m/sになった。仕事をされる前の物体の速さは何か。
①12m/s ②20m/s ③16m/s ④25m/s
【46】発泡スチロール容器に20 ℃の水100 gが入っている。ここに80 ℃のお湯50 gを入れてかき混ぜた。熱平衡に達したとき、全体の温度は何℃になるか。
ただし、水の比熱を4.2 J/(g・K)とし、外部との熱の出入りはないものとする。
①40℃ ②30℃ ③70℃ ④20℃
【47】下図のように、長さlの糸で質量mの小球を吊るし、θの傾きで等速円運動をさせた。このとき等速円運動の速度vを求めよ。ただし、重力加速度をgとし、糸はたゆまないものとする。

①√gl tanθ ②√gl sinθ ③√g sinθ ④√gl sinθtanθ
【48】ある物体に20kNの力を加えたとき、加速度が0.5km/s^2だった。この物体の質量を求めよ。
①20kg ②40kg ③50kg ④10kg
【49】ばね定数39.2 N/mで自然長が0.5 mのばねがある。このばねの一端を天井につけ、もう一端に質量1 [kg]の球を取り付ける。球を静かに離すと運動せずに静止していた。重力加速度が9.8 m/s2であり、ばねの質量を無視できるとき、ばね全体の長さを答えなさい。
①0.75m ②0.8m ③0.25m ④0.5m
【50】2.0×10-6Cと−6.0×10-6Cに帯電したをもつ2つの小球が,0.20mだけ離して置かれている。 クーロン定数を9.0×109N・m2/C2として,この小球間にはたらく静電気力の大きさを求めよ。
①1.8N ②2.0N ③2.7N ④3.6N
解答&解説(間違ってたらごめんなさい)
【1】①
日本とNYの時差は14時間。日本の方が時間が進んでいるため、14時間戻す。
【2】④
10進数は2で割っていき、商と余りを記入して連結。
2)16・・・0
2)8・・・0
2)4・・・0
2)2・・・0
1
【3】②
条件から式を立て、連立方程式を解く。
【4】③
乗務する全員の平均年齢が40歳のことから、全員の年齢の合計は、40×6=240。
一方、客室乗務員の平均年齢は33歳であることから、客室乗務員の年齢の合計は33×4=132。
機長の年齢をx歳とし、副操縦士の年齢が38歳であることを考えると、全員の年齢に関する式は次のように書ける。
240=132+48+x
(全員の年齢の合計)=(客室乗務員の年齢の合計)+(副操縦士の年齢)+(機長の年齢)
よって、x=60となり、機長の年齢は60歳とわかる。
【5】④
3回目に2個目の青玉を取り出すパターンは以下の2パターンが考えられる。

よって、求める確率は 5/108となる。 参考サイト
【6】③
今現在4戦目まで消化して残りは最大3試合である。Aはすでに3勝しているため、残り3戦のうちでAが1勝を上げAの優勝が決まるか、Bが3連勝してBが優勝するパターンしかない。
Aが3勝しているので、
5戦目でAが勝利し優勝 (勝利パターンはA)
6戦目でAが勝利し優勝 (勝利パターンは B,A)
7戦目でAが勝利し優勝 (勝利パターンは B,B,A)
7戦目でBが連勝しBが優勝 (勝利パターンは B,B,B)
よって、5戦目から決着がつくまでのパターンは4パターンである。
参考サイト
【7】②
頭金として支払う額は25%=1/4。この時点での残額は3/4。
ここに10%(=1/10)の利子が付くので、頭金以外に支払う額は
3/4+3/4×1/10=33/40
これを11回に分割して支払うので、1回分の支払額は
33/40÷11=3/40
(参考:「史上最強 SPI&テストセンター 超実践問題集」 ナツメ社)
【8】④
期待値の定義、解答については参考サイトを見てください。
【9】①
露点とは、温度を下げていった時に「飽和水蒸気量=実際に入っている(含んでいる)水蒸気量」となる温度。
この温度は今回のグラフより、5℃とわかる。 参考サイト
【10】①
参考サイト
【11】④
参考サイト
【12】②
参考サイト
【13】②
参考サイト
【14】③
PQ+QG が最も小さくなるのは、下の図1のような展開図で、PG が一直線になるとき。
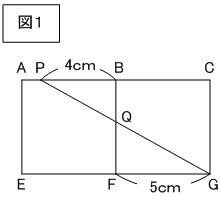
三角形BPQ と三角形FGQ は相似で、相似比は 4:5 なので、BQ の長さは、BF を 4:5 に分ければよく、
5×4/9=20/9 cm
参考サイト
【15】①
参考サイト
【16】②
参考サイト
【17】③
参考サイト
【18】④
上から1段ずつスライスし、どのブロックが貫通しているかを考えていく。
1段目:12個
2段目:11個
3段目:14個
4段目:11個
となり、合計は48個となる。 図解は→参考サイト
【19】④
階差を考えると 2,4,6,8,・・・,2kとなっている。
階差数列の公式(もしくは5項目から足していく)から、第7項は44となる。
【20】①
この数列は公差11の等差数列。
よって第14項は、5+{11×(14-1)}=148。
求める和は、(5+148)×14÷2=1071。
【21】②
(11+20)+(12+19)+(13+18)+(14+17)+(15+16)=31×5=155
(別解) (11+20)÷2×10=155
【22】②
「魔方陣」という問題です。たて・よこ・ななめ、どの線に沿って足してもその合計が同じような方陣のことを言います。
左下のマスに入る数字をイとします。魔方陣の性質から、「8+12+イ」と「9+ア+イ」が等しくなる。
よって、20+イ=9+ア+イ。これを解いて、ア=11。 参考サイト
【23】③
厳密には数Ⅲの範囲ですが、令和三年度でも棒の極限は出題されていたので、類題として出題しました。
文系の方には馴染みないと思うので、捨ててもいい範囲です。詳しく知りたい方は「無限等比級数」などで調べてください。
点Pの座標は、順に次のようになる。
1 , 1-(1/2) , 1-(1/2)+(1/2)^2 , 1-(1/2)+(1/2)^2-(1/2)^3 ,・・・
ゆえに、点Pが近づいていく点の座標をxとすると、xは初項1、公比 -1/2の無限等比級数で表される。
公比 -1/2の絶対値1/2は1よりも小さいので、この無限等比級数は収束して、
x=1/{1-(-1/2)}=2/3
よって、点Pが近づいていく点の座標xは x=2/3
(参考:「数学Ⅲ」 数研出版)
【24】③
参考サイト
【25】②
読んだページ数は、金曜日に4/15。土曜日には残った11/15のうち2/9、つまり11/15×2/9=22/135。
結果、金土では全体の、4/15+22/135=58/135を読んでいる。よって残りは77/135。
全体のページ数をxとすると
73+81=(77/135)x
x=270ページ となる。
残りの81ページは、81÷270=0.3=3割。
(参考:「史上最強 SPI&テストセンター 超実践問題集」 ナツメ社)
【26】③
この場合、二人は「二人の速度の和」の速度で近づく。
速度の和:2.7+3.6=6.3㎞/時
距離:2.7×42/60=1.89km(速さ×時間)
よって出会うまでの時間は、1.89÷6.3=0.3時間→18分。
(参考:「史上最強 SPI&テストセンター 超実践問題集」 ナツメ社)
【27】③
参考サイト
【28】②
(ブラックボックス問題)今回のX装置の場合であれば、入力が3の時、出力が5。入力が-2の時、0が出力されている。このことより、装置Xは+2の処理が行われることがわかる。また、装置Yは、入力が3の時、出力が6で、入力が4の時、8が出力される。このことより、装置Yによって、入力値の2倍の値が出力されることが分かる。
cが78ということは、Yの出力が78ということなので、Yの入力値bは、その1/2の値となる。よって、bは39。更に39は、装置Xの出力値なので、入力値はその-2になるので、37となる。
よって、求める解答は37。 参考サイト
【29】②
小学生1名は、子供料金が適用されるので、0.5a。
中学生1名は、学生割引が適用されるので、0.8a。
大学生1名は、割り引きが適用されないので、a。
よって、全員で一緒に入館する場合は次の金額がかかる。
0.5a + 0.8a + a = 2.3a
【30】③
8月24日と8月26日は、平日・日曜日の料金。8月25日は土曜日の料金である。
1泊目:8月24日(平日)、本館→大人1人 8,000円&子供2人 5,000円×2
2泊目:8月25日(土曜)、本館→大人1人 10,000円ー2,000円=8,000円&子供2人 (6,000円ー1,000円=5,000円)×2
3泊目:8月26日(日曜)、新館→大人1人 10,000円ー2,000円=8,000円&子供2人 (6,000円ー1,000円=5,000円)×2
よって合計は54,000円。 参考サイト
【31】③
それぞれ割合から数を出してもいいが、正確な数値を計算する前に、目星をつけるのもアリ。
12607万人に対し、九州は11.8%であり、その人口は約1487万人。中部は15.5%であり、人口は約1954万人。
よって、15.5%以上の人口割合を持つ地域は、1500万人以上の人口を持つことになり、それらは3つある。 参考サイト
【32】①
(人口密度)=(人口)÷(面積)[人/km^2]
それぞれ計算すると、(単位省略)
イヌ→3.56、ネコ→105.2、トラ→2.13、ライオン→19
よって、3番目に大きい都市は①のイヌ。
【33】②
果樹園の使用面積が9800haということなので、その使用割合は、耕地全体の面積35000haの何%になるかをまず求める。
9800÷35000=0.28
よって、果樹園の使用割合は28%と分かる。その他に牧草地は22%、その他で24%使用しているので、田の使用割合は次のようになる。
(他の使用割合)
=100%-果樹園-牧草地-その他
=100%-28%-22%-24%
=26% 参考サイト
【34】①
右ねじの法則より、ABの中点ではお互いに打ち消し合う向きの磁場ができ、0になる。また、直線電流の周りでは同心円状に磁場が発生する。
【35】④
二乗の数字が並んでいる。抜けている4の二乗が答え。 参考サイト
【36】②
1人分の1日の仕事量を求める。1/3の量を10日間、15人で行ったから、1/3÷10÷15=1/450 残りの作業量は1-1/3=2/3 残りの日数10人で終わらせるために必要な人数をX人とすると、(1/450)×10×X=2/3 これを解くと、X=30 よって必要な増員数は30-15=15人。よって答えは15人。
参考サイト
【37】①
混ぜた後、含まれる食塩:250×0.24+750×0.16=180[g]
混ぜた後の食塩水量:250+750=1000[g]
よって、180÷1000=0.18。18%の食塩水ができる。
【38】④
参考サイト
【39】③
逆方向の流れによって、進む速度は遅くなるので、
(10 − 2) × 3 = 24。よって24km。
【40】③
密度と太さが一様な棒ということは、棒の重心はちょうど真ん中0.5mの位置。
「つりあっている」ということは、支点の左右のモーメントの和はゼロになる。
つまり、モーメントのつりあいの式を作れば良い。
支点と重心の距離は0.1m。質量はまだわからないので、m[kg]とする。このモーメントは0.1×m×g=0.1mgとなる。
物体Aは支点から0.4mの位置に吊されていて、2kg。このモーメントは0.4×2×g=0.8gとなる。
これらがつりあっているので、0.1mg=0.8gより、m=8[kg]となる。
以下【43】まで参考サイト
【41】②
電池の内部抵抗を考える場合、その他の抵抗と電池の内部抵抗は直列つなぎとして考える。
つまりこの問題の場合、回路の合成抵20+1+1=21Ω
回路を流れる電流は9/21=3/7≒0.428…
四捨五入して、0.43Aとなる。
【42】④
「なめらかな斜面」なので、摩擦力は0と考える。
つまり、物体が斜面を滑り落ちようとする力を求めて、同じ大きさの力で引き上げれば物体は静止する。
重力加速度を9.8[m/s^2]とすると、重力は2.0×9.8=19.6N
斜面が30°なので、19.6×sin30°=19.6×1/2=9.8Nの力で斜面に沿って引っ張り上げればよい。
【43】①
Pa(パスカル)の単位は、[N/m^2]とも表せ、かかっている力N(ニュートン)を面積m^2(平方メートル)で割ったもの。
10000mm^2=10000×10^(-6) m^2
よって、圧力は
(3×10^3)/(10000×10^(-6))=3/10×10^6[N/m^2]=0.3MPa
【44】③
電流計より、RとVに流れる電流は0.2Aだとわかる。
電圧計Vの値はオームの法則から
V=25×0.2=5 [V] になる。
抵抗Rにかかる電圧は1Vなので、オームの法則から
R=1/0.2=5 [Ω] になる。 参考サイト
【45】③
(非保存力のした仕事)=(運動エネルギー変化)である。
仕事をされる前の物体の速さをvとすると、
72=1/2×1.0×20^2-1/2×1.0×v^2
となり、v=16[m/s]となる。
【46】①
熱量保存の法則より、計算する。詳しい図解は以下参考サイト。
参考サイト
【47】④
参考サイト
【48】②
単位換算に気を付け、運動方程式より質量mを求める。
【49】①
フックの法則。バネ自体の長さも考慮することを忘れない。
参考サイト
【50】③
クーロン力の簡単な計算。
参考サイト
