SARIMAとLSTMモデルで新型コロナ前後の求人数と失業率の変化を分析する
1.はじめに
1.1 検証内容
新型コロナウィルスが日本で観測された2020年1月以来、執筆時点では4回の緊急事態宣言やまん延防止等重点措置などを経て経済は混乱し、国民の動きにも多大な影響を及ぼしています。
今回SARIMAとLSTMを用いて新型コロナウィルスが求人数と失業率にどのようにインパクトを与えているかを分析します。
1.2 実装環境
・MacBook Pro
・Google Colaboratory
・Python
2.データ前処理
2.1 データソース
今回検証に使用するデータは以下のとおりです。
①一般職業紹介状況(厚生労働省)
新規求人数(実数、季節調整値)
公共職業安定所(ハローワーク)における新規求人数の推移。今回は実数のみ使用。
②労働力調査(総務省)
主要項目(労働力人口,就業者,雇用者,完全失業者,非労働力人口,完全失業率)
2.2 前処理
①求人数
エクセル形式でダウンロードとなるので、あらかじめ3つのシート(求人数全体・求人数パート除く・求人数パート)をそれぞれcsvでエクスポートする。季節調整値は今回使用しないので、月ごとの実数のデータのみが残るように手動で調整します。
DataFrameでcsvを読み込んだ後、最終的にはindexを月ごとの時系列にしたいので、以下のコードで1~12月の各月がカラムになっているものを「○○年○月」という形式になるように加工します(本当はdatetimeにするだけで大丈夫です)。またこの時点で数値データの型をstrからfloatに変更します。3つシートがあるのでそれぞれ同様の処理をします。
new_index1 = []
data1 = []
for index, row in df.iterrows():
for col in df:
new = index + col.translate(str.maketrans({chr(0xFF01 + i): chr(0x21 + i) for i in range(94)}))
newdate = datetime.strptime(new, '%Y年%m月').strftime('%Y年%-m月')
new_index1.append(newdate)
data1.append(row[col])
df_all = pd.DataFrame(data1, columns=['求人数all'], index=new_index1).apply(lambda x: x.str.replace(',','')).astype(np.float)②労働力調査
こちらについてもエクセルから必要なcsvを取り出しますが既にindex部分が年+月のような形式になっているので書式などを①に揃えます。またデータの中に数値以外の文字が入っている箇所があるので以下のコードで排除し、同時にstrからfloatに変更します。
df = df.iloc[1:,2:].dropna()[df['労働力人口.1男']!="… "].apply(lambda x: x.str.replace('<','').str.replace('>','')).astype(np.float)最後にこれらを組み合わせたDataFrameを作成します。
all_data = df_all.join(df_fulltime).join(df_parttime).join(df).dropna()3.学習モデルの作成
3.1 SARIMA
SARIMAモデルでDataFrameの中から「求人数all」と「完全失業率(%)男女計」それぞれの時系列解析を行なっていきます。
方針としては、検証データがちょうど新型コロナの期間である約24ヶ月の倍の48ヶ月間になるようにして、検証データ前半と後半に分かれるようにし、検証結果と実数値の平均二乗誤差をそれぞれ比較します。
import pandas as pd
train_df = all_data.loc[:"2018-01-01",:] #学習に使うデータ
test_df = all_data.loc["2018-02-01":"2019-12-01",:] #下と同じデータ量
covid_df = all_data.loc["2020-01-01":,:] #上と同じデータ量3.1.1 最適なパラメータの決定
まずSARIMAモデルの学習に必要なパラメーターを情報量規準 (今回の場合は BIC(ベイズ情報量基準))によってどの値が最も適切なのか調べるプログラムを実行します。
import warnings
import itertools
import pandas as pd
import numpy as np
import statsmodels.api as sm
# 関数の定義
def selectparameter(DATA,s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs,results.bic)
except:
continue
return parameters[np.argmin(BICs)]
params_all = selectparameter(train_df["求人数all"],12)
# [(0, 0, 1), (1, 1, 1, 12), 12518.126290358296]
params_unemployed = selectparameter(train_df["完全失業率(%)男女計"],12)
# [(0, 0, 1), (1, 0, 1, 12), -706.8919674778896]3.1.2 SARIMAモデルの構築と学習・予測の可視化
パラメータが決定したらそれらを用いて実際にSARIMAモデルを構築し学習させ、予測結果を可視化します。
まずは求人数から可視化します。
SARIMA_job_offers = sm.tsa.statespace.SARIMAX(train_df["求人数all"],order=params_all[0],seasonal_order=params_all[1]).fit()
#コロナ前の期間で予測
pred_before_covid = SARIMA_job_offers.predict("2018-02-01","2019-12-01")
#コロナ禍の期間で予測
pred_after_covid = SARIMA_job_offers.predict("2019-12-01","2021-11-01")
plt.figure(figsize = (20,10))
plt.title("求人数推移")
plt.xlabel("time(year)")
plt.ylabel("求人数")
plt.plot(all_data["求人数all"], label='求人数実数値')
plt.plot(pred_before_covid, color="y", label='pred_before_covid')
plt.plot(pred_after_covid, color="r", label='pred_after_covid')
plt.legend(loc='lower right')
y = [i*1e6 for i in all_data.values[:, 0]] #自動で指数表記になるので直しています
plt.ticklabel_format(style='plain',axis='y')
plt.show()
続いて完全失業率について同様のプログラムを実行します。
SARIMA_unemployment_rate = sm.tsa.statespace.SARIMAX(train_df["完全失業率(%)男女計"],order=params_unemployed[0],seasonal_order=params_unemployed[1]).fit()
pred_before_covid_ur = SARIMA_unemployment_rate.predict("2018-02-01","2019-12-01")
pred_after_covid_ur = SARIMA_unemployment_rate.predict("2019-12-01","2021-11-01")
plt.figure(figsize = (20,10))
plt.title("完全失業率推移")
plt.xlabel("time(year)")
plt.ylabel("完全失業率(%)")
plt.plot(all_data["完全失業率(%)男女計"], label='完全失業率実数値')
plt.plot(pred_before_covid_ur, color="y", label='pred_before_covid')
plt.plot(pred_after_covid_ur, color="r", label='pred_after_covid')
plt.legend(loc='lower right')
plt.show()
3.1.3 定量的な分析
出力結果から、求人数はSARIMAモデルの予測と比べ大幅に減っており、完全失業率は増えているという結果が見えました。
これらを定量的に評価するためにそれぞれの平均二乗誤差を計算します。
from sklearn.metrics import mean_squared_error
y = all_data.loc[pred_before_covid.index,["求人数all"]]
print(np.sqrt(mean_squared_error(y, pred_before_covid)))
#64904.80561364783
y = all_data.loc[pred_after_covid.index,["求人数all"]]
print(np.sqrt(mean_squared_error(y, pred_after_covid)))
#314080.8744289107
y = all_data.loc[pred_before_covid_ur.index,["完全失業率(%)男女計"]]
print(np.sqrt(mean_squared_error(y, pred_before_covid_ur)))
#0.18625373050497893
y = all_data.loc[pred_after_covid_ur.index,["完全失業率(%)男女計"]]
print(np.sqrt(mean_squared_error(y, pred_after_covid_ur)))
#1.0269470978005957出力結果を四捨五入しまとめると以下のようになり、両方でコロナ禍の方が誤差が大きいという結果が表せました(この後LSTMモデルでも平均二乗誤差を出力します)。
求人数
・コロナ前:64,904.8
・コロナ禍:314,080.9
完全失業率
・コロナ前:0.186
・コロナ禍:1.027
3.2 LSTM
次にLSTMモデルでも時系列解析を行なっていきます。こちらでもSARIMAモデル同様に「求人数」と「完全失業率」について分析を行なっていきますが、データセットの中のその他のカラムを説明変数として学習させます。
3.2.1 LSTMモデルの構築と学習・予測の可視化
一旦csvで保存したall_dataを読み込む際に説明変数として使わない目的変数と相関がありすぎるカラムはドロップしています(seabornのheatmapで相関を確認すると良いです)。またSARIMAモデルの解析とある程度合わせるために検証データがコロナ禍と合うようにして、それぞれ平均二乗誤差を出力しています。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import math
all_data = pd.read_csv('/all_data.csv', index_col=0).drop(['求人数full', '求人数part','労働力人口男女計','就業者男女計','雇用者男女計','完全失業者男女計','非労働力人口男女計'], axis=1)
dataset = all_data.copy().values
#訓練データ・検証データの作成
train_size = int(len(dataset) * 0.94)
# 訓練データ、検証データに分割
train, test = dataset[0:train_size, :], dataset[train_size:len(dataset), :]
# データのスケーリング(正規化)を行います
# 最小値が0, 最大値が1となるようにスケーリング方法を定義します
scaler = MinMaxScaler(feature_range=(0, 1))
scaler2 = MinMaxScaler(feature_range=(0, 1))
# `train`のデータを基準にスケーリングするようパラメータを定義します
scaler_train = scaler.fit(train[:,1:])
# パラメータを用いて`train`データをスケーリングします
train[:,1:] = scaler_train.transform(train[:,1:])
# パラメータを用いて`test`データをスケーリングします
test[:,1:] = scaler_train.transform(test[:,1:])
kyujin_scaler = scaler2.fit(train[:,[0]])
train[:,[0]] = kyujin_scaler.transform(train[:,[0]])
test[:,[0]] = kyujin_scaler.transform(test[:,[0]])
# 入力データ・正解ラベルを作成する関数を作ります
# data_X:入力データ。nヶ月分のデータを1セットとする
# data_Y:正解ラベル。Xの翌月を正解とする
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back):
xset = []
for j in range(dataset.shape[1]):
if j != 0:
a = dataset[i:(i+look_back), j]
xset.append(a)
dataY.append(dataset[i + look_back, 0])
dataX.append(xset)
return np.array(dataX).transpose(0, 2, 1), np.array(dataY)
# 入力データが何ヶ月のデータを取るかを定義します
look_back = 12
# 作成した関数`create_dataset`を用いて、入力データ・正解ラベルを作成します
train_X, train_Y = create_dataset(train, look_back)
test_X, test_Y = create_dataset(test, look_back)
# LSTMネットワークの構築
model = keras.Sequential()
model.add(layers.LSTM(30, input_shape=(look_back, train_X.shape[2])))
model.add(layers.Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
# LSTMネットワークの訓練(学習)
model.fit(train_X, train_Y, epochs=30, batch_size=1, verbose=2)
# 読み込みデータに対する予測値を出力します
train_predict = model.predict(train_X)
test_predict = model.predict(test_X)
# 訓練データからの予測値と訓練データを元に戻します
# train_predict = train_predict.reshape(-1)
train_predict = kyujin_scaler.inverse_transform(train_predict)
train_Y = kyujin_scaler.inverse_transform(train_Y[:, np.newaxis])
# 検証データからの予測値と検証データを元に戻します
test_predict = kyujin_scaler.inverse_transform(test_predict)
test_Y = kyujin_scaler.inverse_transform(test_Y[:, np.newaxis])
# 訓練データから予測したデータの整形
train_predict_plot = np.empty_like(dataset[:, 0]).reshape(-1,1)
train_predict_plot[:, :] = np.nan
train_predict_plot[look_back:len(train_predict)+look_back, 0] = train_predict[:, 0]
# 検証データから予測したデータの整形
# 既存の配列`dataset`と同じ大きさ(行数・列数)、データ型で
# 値を0に初期化したプロット用の空の配列を作成します
test_predict_plot = np.empty_like(dataset[:, 0]).reshape(-1,1)
# 空の配列のすべての値を欠損値`nan`にします
test_predict_plot[:, :] = np.nan
# 訓練データの予測値と位置を合わせます
test_predict_plot[len(train_predict)+(look_back*2):len(dataset), 0] = test_predict[:, 0]
# データのプロット
plt.figure(figsize = (20,10))
plt.title("求人数推移")
plt.xlabel("time(month)")
plt.ylabel("求人数")
# 読み込んだままのデータをプロットします
plt.plot(all_data.values[:, 0], label='dataset')
# 訓練データから予測した値をプロットします
plt.plot(train_predict_plot, label='train_predict')
# 検証データから予測した値をプロットします
plt.plot(test_predict_plot, label='test_predict', color='r')
x = all_data.index
y = [i*1e6 for i in all_data.values[:, 0]]
plt.ticklabel_format(style='plain',axis='y')
plt.legend(loc='lower right')
plt.show()
コードは省略しますが「完全失業率」でも同様に学習させプロットします。完全失業率と相関の強い「失業者数」などもドロップしています。
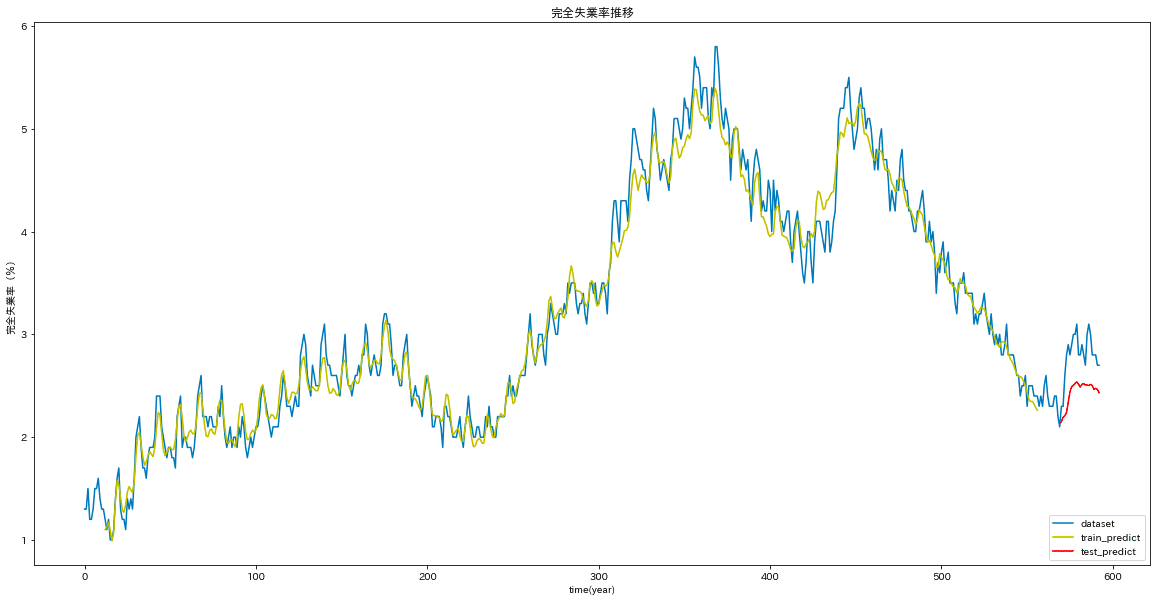
3.2.2 定量的な評価
先ほどのコードの平均二乗誤差は以下の通りになりました。カッコ内はSARIMAモデルの際の結果です。
求人数
コロナ前:54,634.9(64,904.8)
コロナ禍: 123,105.3(314,080.9)
完全失業率
コロナ前:0.17(0.186)
コロナ禍:0.39(1.027)
4.まとめ
SARIMAモデルとLSTMモデルそれぞれ使い「求人数」と「完全失業率」を解析しました。両方のモデルにおいてそれぞれ予測結果とコロナ禍のデータは乖離するということが定量的にも確認でき、大きなインパクトがあったと言えそうです。
また今回のデータにおいてはSARIMAモデルよりもLSTMモデルの方が精度が高いということも可視化することができました。
