第三回 バッティングフォームの違い (2021年1月8日)

今回から、「捻りモデル」と「回転モデル」のバッティングフォームの違いについて説明します。まずは、それぞれの理論に基づいた理想的なフォームの違いについてです。
上図の右が「ベースボールの物理学」でR.Adair教授が紹介している「回転モデル」のバットの軌道で、左が「捻りモデル」のバットの軌道です。「回転モデル」の軌道も悪くなさそうに見えますね。そこでイラストだけではわかりにくいので人のイラストを加えてみるとこうなります。
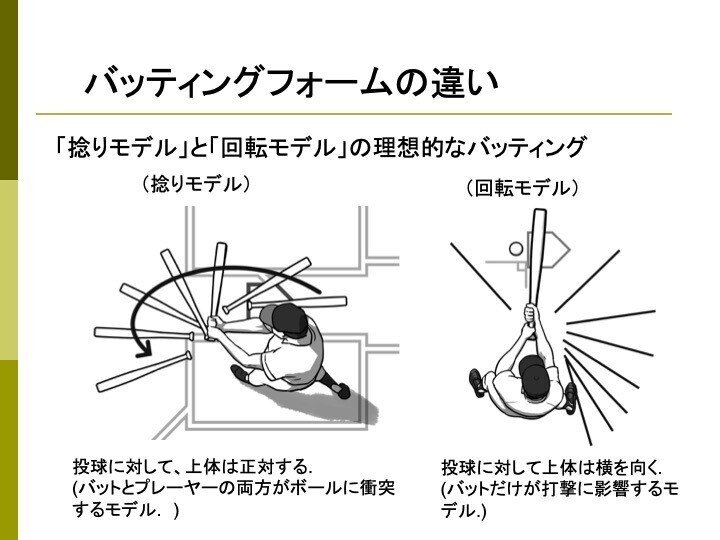
左の「捻りモデル」の理想形は、テッド・ウイリアムズを右打ちに反転させてバットの軌道をトレースしたものです。右の「回転モデル」の理想形では、ボールに差し込まれて選手の手がいかにも痛そうです。

これら動作をさらに簡略化して、シンプルにモデル化してみました。
第二回で、壁に釘を打つ動作を例に、「捻りモデル」はトンカチを持って打つモデルと説明しましたが、最初は板バネをしならせてエネルギー(以下「力」とします。)を溜めボールを打つ板バネモデルがわかりやすいでしょう。ここでのポイントは力です。
別の言い方では、釘に対してどれだけ大きな「仕事」(力x距離)をするかがポイントなので、バットと選手が一体となり、どれだけ大きな「力」を出すことができるかがポイントということです。
「回転モデル」はトンカチを釘に投げてぶつけるモデルなので、トンカチをどれだけ速いスピードで釘にぶつけるかが課題になります。ここでのポイントは、振り回すバットの速度です。
そこで少し力と速度の関係について考えてみましょう。

板バネが手元にないので、代わりに裏庭で取ってきた猫じゃらしを使いましょう。猫じゃらしのフサを右方向に、手を左方向に、反対方向動かすと猫じゃらしはしなります。これ以上は動かないというところまでしならせると、猫じゃらしには「力」が最大限溜まっています。
ではその状態、「力」が最大の状態で猫じゃらしのフサの速度はどれくらいでしょうか?最大限しなったところではフサは動いていないので、猫じゃらしのフサ速度はゼロです。

手を動かしならが猫じゃらしを反対方向に弾いてみましょう。フサは速度を上げて反対方向に向かい、速度が上がった分、茎の「力」は抜けていきます。最終的に反対方向にしなりフサは止まりました。フサ速度はまたゼロになり反対向きに力が最大限溜まっています。
この行程で、猫じゃらしのフサ速度が最大になったのはどこだったでしょうか?フサ速度が最大になったのは、猫じゃらしの茎が真っ直ぐになった時で、この時猫じゃらしの茎に溜まった「力」、茎力がゼロになります。
基本的に速度が最大の時に力はゼロになり、最大の力を出す時に速度はゼロになるという関係があります。
(難しい言い方をすると力は(加速度x質量)で表されますが、速度を微分したものが加速度という関係があるので、速度最大の時に加速度最低、つまり力が最低になるということです。)
改めて上図イラスト見てみましょう。「回転モデル」が猫じゃらしのフサ速度Maxのところで打つモデルであることがわかるでしょう。「捻りモデル」は少しわかりにくいですが、猫じゃらしの茎力Maxで打つモデルです。
「捻りモデル」が少しわかりにくい理由は、人間の体は金属の様に硬いものではないので、力と速度の関係にズレが生じており、少しバットを振り出したところで力が最大になっているからです。
つまり「捻りモデル」は、打撃ポイントでのバットスピードは最低に近く、バットスピードが最大になるのは、フォロースルーのあたりになるモデルです。これは実践で得られた「インサイドアウトにコンパクトに打ち、フォロースルーを大きく(バットスピード最大にする)」という経験則と非常によく合っています。
ついでに、もう一点指摘しておきたい点があります。
第二回で紹介したDynamics of the baseball-bat collisionであるとか、Model of baseball batsといったレポートの「特定の条件」についてです。
上記2枚目のイラスト右の「回転モデル」の絵と猫じゃらしの「フサ速度」と「茎力」を使って説明してみましょう。
「回転モデル」のイラストと猫じゃらしを重ねてみると、「回転モデル」の理想的なバッティングフォームは、フサ速度最大かつ茎力がゼロであることがわかるでしょうか。これは体幹からの「力」(茎力)が全てバット速度(フサ速度)に変わっている状態です。
体幹からの力がゼロなので、この条件でいくら客観的な実験を行っても、当然ボールに対して力学的には「仕事」をするといった現象は、例えば誰がやろうと確認できるわけがありません。
この様に、実験の結果や報告というのは、条件やデータの切り取り方によって変わってきます。自分の直感や感覚と違う「データ」で出てきた時は、注意してみましょう。直感や感覚が正しい事はよくあると思います。
最後に、バッティング動作における「捻りモデル」の理想形と「回転モデル」の理想形の違いについてまとめておきます。

次回からは、これら具体的な動作について解説しましょう。「フサ速度」と「茎力」という言い方が気に入ったので、また使うかもしれません。
