
Blenderでフラクタル構造を再現する
はじめに
ジオメトリーノードの使用して、フラクタル構造を再現します。
そのためのモチーフとして、ロマネスコという植物を今回は再現しますが、
再現のためのプロセスは他のフラクタルにも流用できると考えています。

https://pin.it/1I6kvxo
ただ僕の技術ではロマネスコ風(5%)のようなものしかできなかったので、
このプロセスを元に100%をいつか誰かが完成してくれることを願ってます。
完成品はこのnoteのバナーになっています。
フラクタルとは、
フラクタルとは、『部分が全体と相似(自己相似)となるような図形』で、
ロマネスコで言うと、全体の形と個々の突起の形状が相似になっていることに気づけるでしょう。
ジオメトリーノードの概観
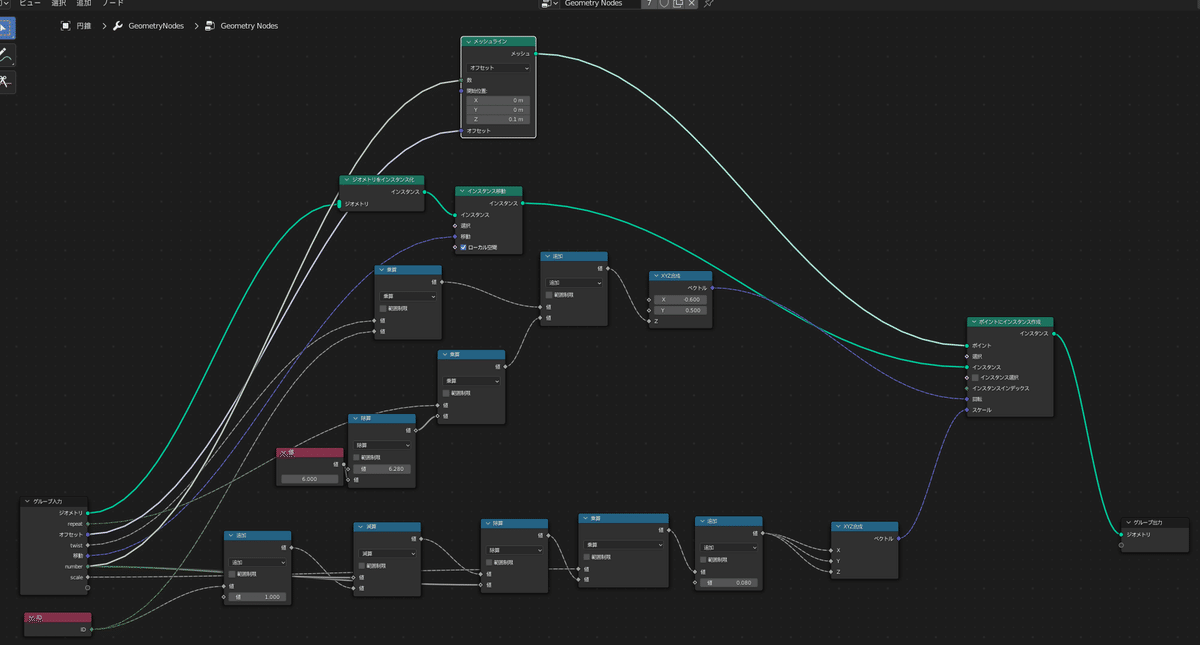
ここから部分部分に分けて解説していきます。
このノードでできるのは下図まででここからさらにほかのジオメトリを
跨いで作業していきます。
グループ入力のパラメーター
上記の概観の中にグループ入力というノードの中にジオメトリ以外のパラメーターがあると思います。これは、ここにつなぐことで、モディファイヤープロパティで一括で値を変化させることができる利点があります。
すべての定数でやる必要はありませんが、微調整が必要なパラメーターは
ここにつなげておくといいと思います。
このオブジェクトのパラメーターは最後に記述しますが、
自分で動かして理想のオブジェクトを作ることを推奨します。
ジオメトリーノードで配列を作る
この部分は以下の記事を参考にさせてもらいました。
まずは大まかな流れとして下図があることを頭に入れておきましょう

ポイントにインスタンス作成
配列を作る際に必要な知識にポイントとインスタンスがあります。
これは、ポイントで最初の形に点を設置し、
その点にインスタンスと呼ばれるメッシュを配置していきます。
これを行うのがポイントにインスタンス作成というノードです。
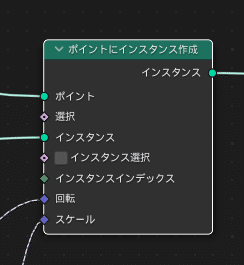
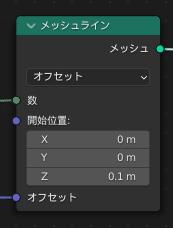
メッシュライン
まずは、ポイントを整列させていきます。そのためのノードが
メッシュラインで指定した間隔で任意の数メッシュを配置していきます。
モディファイアプロパティにおける配列に似た働きをします。
ジオメトリをインスタンス化 , インスタンス移動
先述したメッシュラインでは配列の幅を指定できるだけで、細かな位置調整ができません。
そのため、インスタンス移動というノードを使いたいのですが、
グループ化のジオメトリから直接つなげることはできないため、
ジオメトリをインスタンス化でインスタンスにすることで解決します。
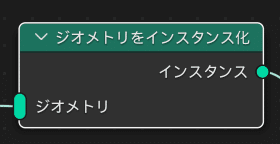
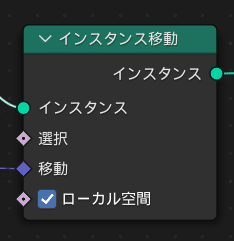
以上を下図のように結ぶと配列の準備は完成です。

個々の要素を回転させる
ここで必要なノードは下図のようになります。
また、グループ入力 / 出力 , ポイントにインスタンス作成の3つのノードは
先にあげたものと同じものです。

ID
配列で複数生成した要素は自動で割り振られたIDを持ちます。
今回の場合は、下の要素から順番に0, 1, 2, …となっています。
また、IDの値を加工しても、要素と加工後の値は結びついているため、
IDを編集しているのではなく、IDの値を編集していることを忘れないでください。

数式
数式ノードは、プルダウンから四則演算や三角関数を指定して、数値を計算させるノードです。
今回は、IDの値を用いて回転をひとつづつ指定したいのですが、
IDの値単体だと、1ずつしか変わりがないため、度数法を用いると1°の差、
弧度法を用いても約60°(1ラジアン)の差であるので、
数式ノードで乗算を選択し、IDの値を任意の定数分離してあげるという操作をします。
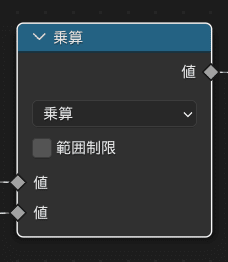
XYZ合成
ひとつづつの要素が回転する角度の値をここまでIDから加工してきました。
しかし、この値を最終的にポイントにインスタンス作成ノードの回転に
接続するのですが、回転の軸はXYZの3パラメーターに対して、
ソケットは1パラメーターであることに気づくと思います。
そのために、3つのパラメーターをベクトルを用いて
1パラメーターにまとめるためのノードがXYZ合成です。
今回のロマネスコでは、XYの回転は固定していいですが、
この部分は作りたいフラクタルの構造を見て、変化します。
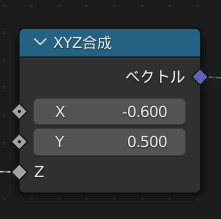
個々の要素の大きさを変化させる
ここで必要なノードは下図のようになります。
また、先ほどと同様に、グループ入力 / 出力 , ポイントにインスタンス作成に加えIDの4つのノードは同じものを使用しています。

数値の加工の流れ
上の流れを見ていただくと、ここまでに説明したノードで完結しているのが分かるでしょう。
そのため、ここではIDを用いて大きさを変化させるための方法を解説します。
まずは一旦ノードなしで大まかな流れを考えましょう。
今ある手持ちの数は、IDの値でこれは1づつ増えていきます。
加えてもう一つが、何個要素を並べるか決めたときの要素の総数です。
この2つを用いて、IDを総数で割るとIDが増えていくたびに一定量増加し、
最終的に1になるという流れができます。ただ、このままだと、
IDは0からスタートするため、0 / n, 1 / n, … (n - 1) / nとなるため、
IDの値に1を足して始めます。また、望む大きさの変化は、
下が大きく上が小さいため、最終的にn - (ID + 1) / n が一般項になります。
以上から、左から3つ分の数式ノードについては理解ができたと思います。
次に、4つ目のノードは、任意の定数tをかけることにより、0 < x <= 1の範囲のデータが、0 < tx <= tと拡張されます。
その後、5つ目のノードで任意の定数kを足すことにより、
k < tx + k <= t +kとなりすべての範囲をカバーできます。
角を作る
下準備
ここまでつくったものは角の形状の部品のため、これを1つの角にします。
そのためには、今ある部品を円状に回せばいいので、回転のためのノードの
乗算とXYZ合成の間に数式(加算)ノードを挿入。
残った接続部とグループ入力のパラメーターを接続します。
(僕は整数型にし、repeatというパラメーター名を付けています。)
また、円状に回す際の一周は、Blenderがラジアンを採用しているため、
2π≒6.28です。これを踏まえて、先ほど追加した、数式(加算)ノードとグループ入力のパラメーター(僕で言うrepeat)の間に下図のようなノードを追加します。
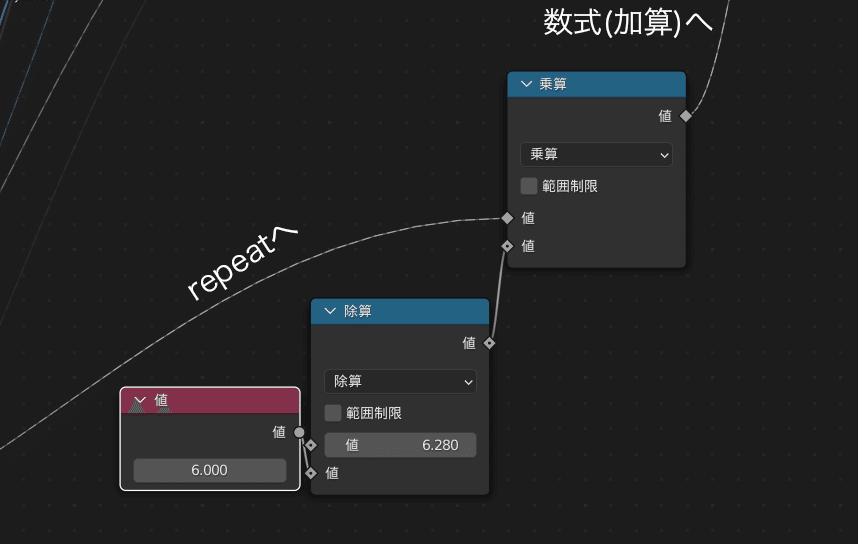
ここで、除算の中の6.28は2πを表し、
値は、いくつの部品で角を作るのかという任意の定数です。
本題
次に、同じ作業を繰り返して角を作るため、
効率化のために新しいジオメトリーノードグループを作成します。
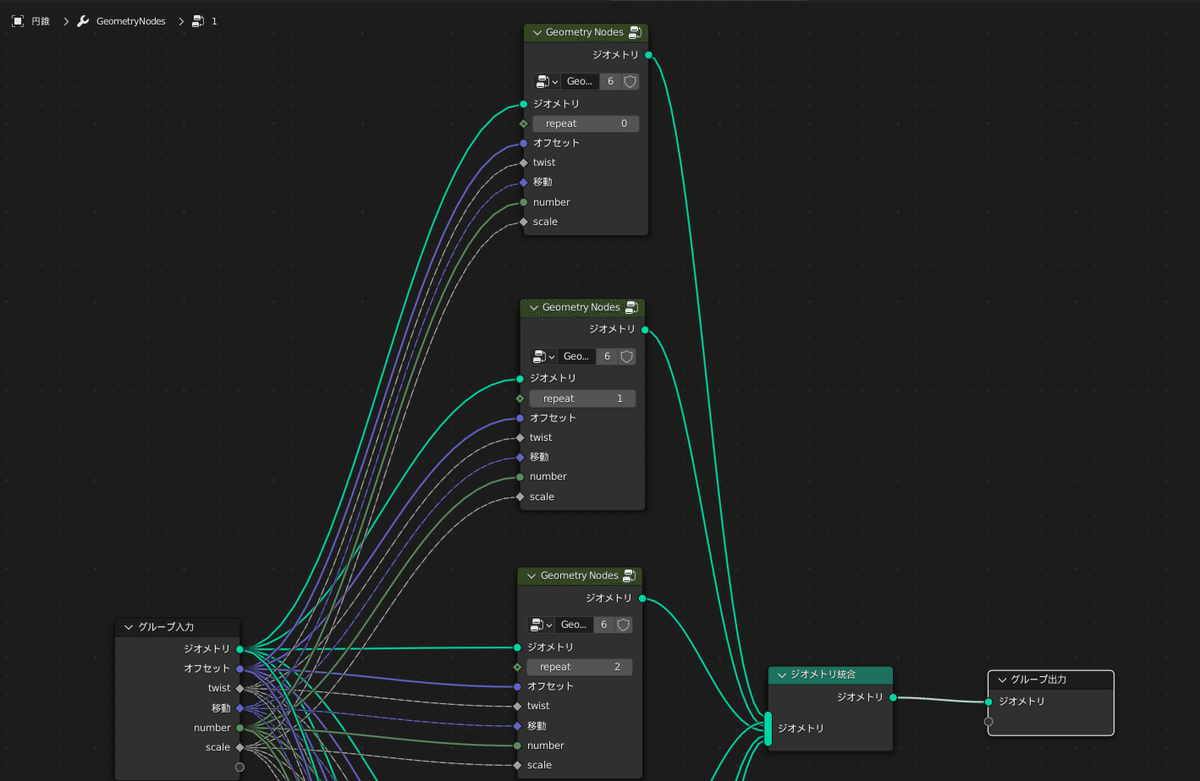
以上が概観で、グループ入力の次のGeometry Nodesというノードは
他のジオメトリーノードグループを呼び出すノードで、
ジオメトリ統合というノードは複数のノードの出力をまとめる働きをします。
ここの肝は、先ほどのパラメーター(僕で言うrepeat)を上から0, 1, 2 …と
入力し、先ほど設定した値の定数分のGeometry Nodesを作成することです。
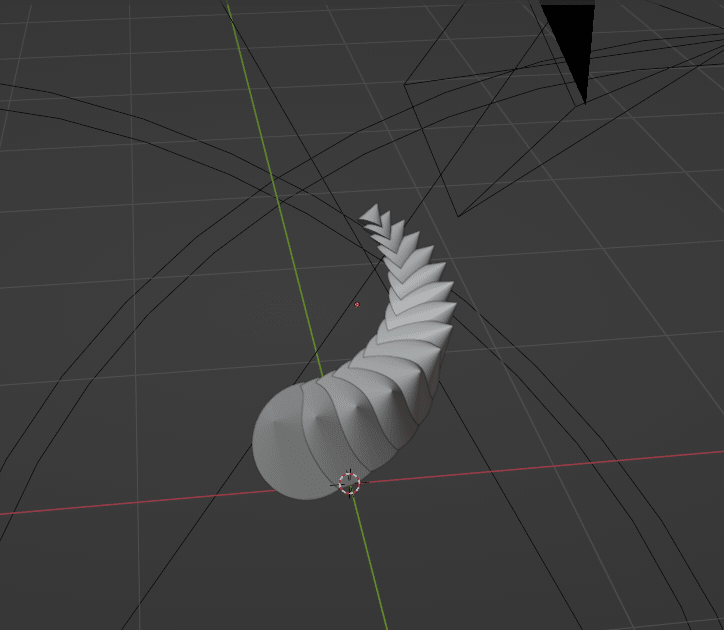
これによって、下図のような角が完成すると思います。
(パラメーターは毎度リセットされてしまうので、デフォルト値に設定するかメモをしておくことを推奨します。)

オブジェクトを作る
ひとつ角ができたので、あとは、この角にさらに角を作るという同じ操作を行えばいいですね。
そのためには繰り返しの作業なので、先ほど同様に新しいジオメトリーノードグループを作ります。
概観は以下のようになります。
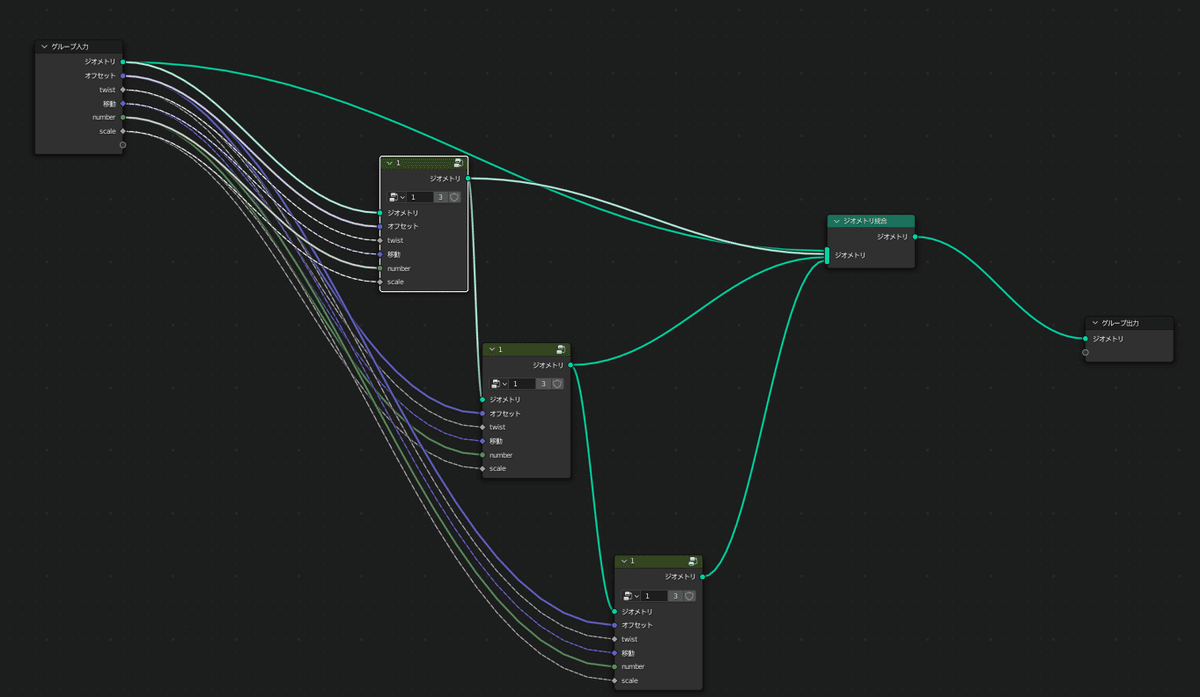
今回のGeometry Nodesノードには角を作ったジオメトリーノードグループを指定してください。
フラクタルをつくる一番の肝は、ここで、Geometry Nodesノードを直列につなげることだと思っています。
ここでパラメーター再設定しなおせばおそらく完成したものだと思います。
最後に
ここまでお疲れさまでした。
ノードの接続などわからない箇所がありましたら、
コメントに書いていただればお答えできる範囲で回答します。
