ラグランジアンの意味

解析力学の最初に出てくるラグランジアン(Lagrangian)は, 最も物理学徒を悩ませるタネの一つだと思う. 

ここでは古典力学の範囲で, このラグランジアンの意味を考察し, 一つの解を提示する. 

[TLDR]

● ラグランジアンは ”エネルギーの偏り具合” の指標である. 
● 最小作用の原理は "自然界の物体は有限時間の間の正味のエネルギーの偏りが最もポテンシャルエネルギーに偏るように運動をする" と解釈できる. 
● 最小作用の原理は運動方程式の再解釈である. 

■ なぜラグランジアンは不思議か

ラグランジアン L の定義は以下の通りです. 

K が運動エネルギー（kinetic energy）, Uがポテンシャルエネルギー(potential energy)です. 

なんでエネルギーの差を取るんでしょうか. 

運動エネルギーもポテンシャルエネルギーもエネルギーとしては等価だからこそ, エネルギー保存則が論じれるわけなので, その差を取ることにどんな意味があるのかは謎に包まれます. 

しかも最小作用の原理（ハミルトンの原理）によるとこのラグランジアンがわかると, 古典力学の支配方程式の一つである運動方程式が導出できるというから驚きなわけです. 

なお, q は座標系に依存しない一般化座標です. 

だた, 注意しなければいけない点は, ラグランジアンはエネルギーの差分で表現されますが, その実態は関数であるという点です. 

さて, これを踏まえて, ラグランジアンの意味に迫っていきます. 

■ ヒントになる例え話

ラグランジアンの正体に迫る前に, この記事を書くきっかけになった, ある教授がはなしてくれた例え話をします. 

ある少年がアルバイトと親からの仕送りで生活しているところを想像してください. 

その少年は x月にはアルバイトで7万円, 仕送り3万円, 合わせて10万円が手に入ったそうです. 

しかし y月にはテスト勉強で忙しく, アルバイトで 4万円しか稼げなかったそうです. そのため, 仕送りをお多めに6万円もらって, この月も合計10万円が手に入ったそうです. 

x月： 7万円（バイト）+ ３万円（仕送り）＝ 10万円
y月： 4万円（バイト）+  6万円（仕送り）＝ 10万円
→ どちらも獲得金額は変わらない...！

しかし, どんな形であろうと, その総額は変わりません. 

ではバイト代と仕送りの差額を見てみるとどうでしょうか. 

x月： 7万円（バイト）- ３万円（仕送り）＝ 4万円
y月： 4万円（バイト）-  6万円（仕送り）＝ -2万円
→ こちらの方が情報が多い. 

x月とy月で値が異なるので, この２ヶ月の間で何かが違うことが数字として現れます. 

この数字を見れば, その金額が多い方がバイトと仕送りど面に収入が偏っているかがわかり, 正負によってどちらに偏っているかわかります. 

つまり, 和を取る場合より差分を見てやったほうが得られる情報が多いようです...

■ ラグランジアンの意味

少し例え話を丁寧に描きすぎてしまったので, 本題に移ります. 

結論から言うと, ラグランジアンと言うのはエネルギーの偏り具合です. 

ラグランジアンの定義は

だったわけですから, その値が正であれば, 絶対値の大きさ分だけ運動エネルギーに偏っているし, その値が負であれば, 絶対値の大きさ分だけポテンシャルエネルギーの方にエネルギーが偏っている. と言うことができます. 

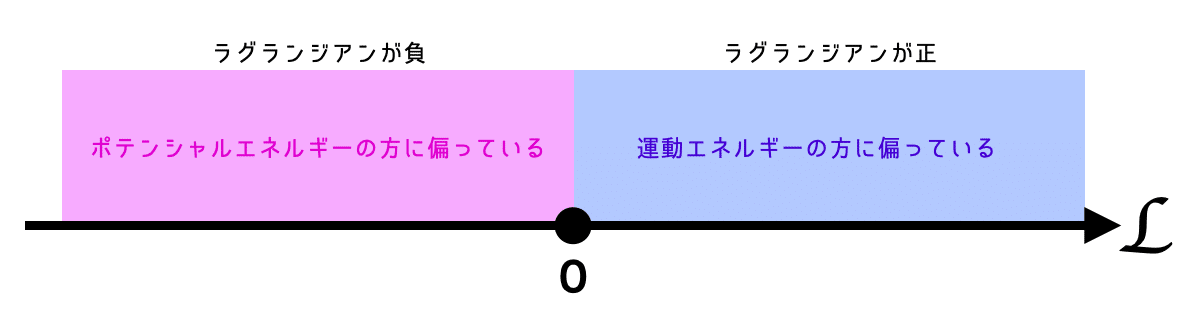
このラグランジアンという量だけから, 運動方程式が導けるということは, 運動のルールを一意に決めるのに必要だったミニマムな情報がエネルギーの偏り具合だった. ということに他なりません. 

さて, 最小作用の原理の方もこの視点で見てみることにしましょう. 

■ 最小作用の原理の意味

さて, 最小作用の原理は ”作用Sの変分が最小になるような経路（座標と速度の時間変化）が解である” ということを主張しています.  

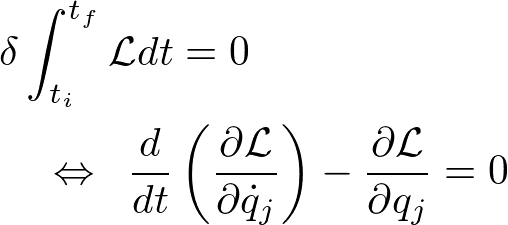
ひとつずつ見ていきましょう.　

まず作用Sの定義は, 

この式の意味するところは, 作用というのは位置と速度が時事刻々と変わっていく間の以下の領域のことだということです. 

これは先ほどのラグランジアンの意味を考えれば, 作用というのは有限時間の間全体での正味のエネルギーの偏りであるということができることになります. 

さて, 作用の変分が０だということは, 多くの場合, 作用が最小値であるということと同等です. 

作用が最小ということは有限時間のエネルギーの偏りの値が最小だ

ということです. ラグランジアンエネルギーがポテンシャルエネルギーの方に偏っていればいるほど小さくなりましたね. 

すなわち先に出た作用の定性な解釈を使うと

最小作用の原理というのは,
自然界の物体は有限時間の間の正味のエネルギーの偏りが最もポテンシャルエネルギーに偏るように運動をする. 

と解釈することができるわけです. 

実際にそうなっているか見てみることにしましょう. 

■ 落体で考えてみる

落体の例で考えてみます. 

自由落下する物体は, 速度ゼロから徐々に徐々に速度を増していき. 地面に着地します.

この, すぐに早い速度で落ちるのではなく, 徐々に速度を上げる様子はまさに "ポテンシャルエネルギーに偏った状態ができるだけ長くなるように運動する" ということを意味してます. 

以下の図を見るとわかりますが, 赤い線で表現されている実際の運動が最も作用Sが小さくなっています. 

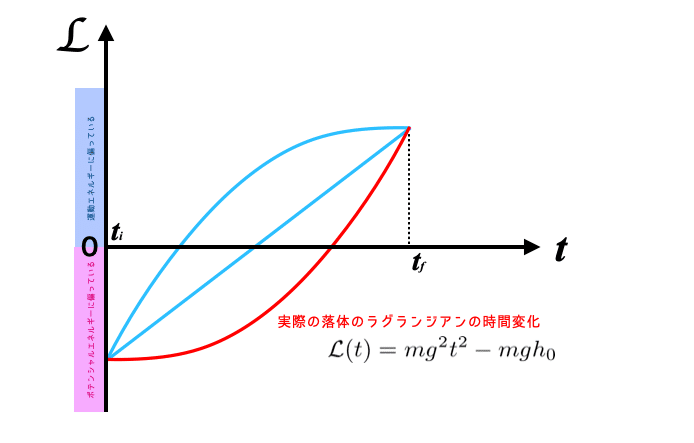
すなわち, 最小作用の原理というのは

運動方程式の "物体に働く力はか速度に比例する形で速度を変化させる" 

という法則を 

”物体は可能な限りポテンシャルエネルギーに偏る” と解釈し直したものなわけです. 

【まとめ】
● ラグランジアンは ”エネルギーの偏り具合” の指標である. 
● 最小作用の原理は "自然界の物体は有限時間の間の正味のエネルギーの偏りが最もポテンシャルエネルギーに偏るように運動をする" と解釈できる. 
● 最小作用の原理は運動方程式の再解釈である. 

いいねしてくれると, これ書いてる人が喜びます.