数列４（数学的帰納法）

書き間違いがあったらコメントにてお願いします。

１．帰納法とは

・帰納法とは、具体的な例から抽象的な性質を導く論理的な手法である。

・たとえば、「とちおとめは赤い」「紅ほっぺは赤い」「あまおうは赤い」…から「いちごは赤い」という結論を導くのが帰納法である。

帰納法の例：いちごは赤い

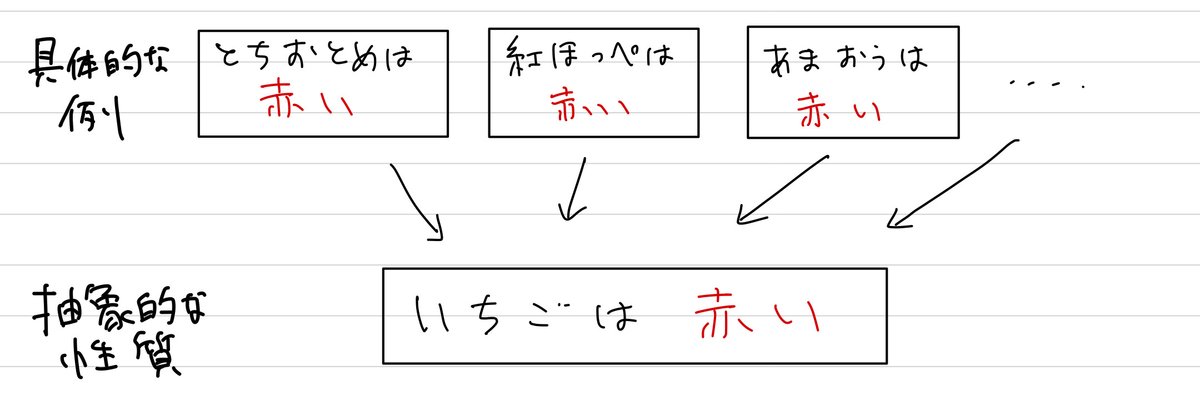
・これは身近な言葉でいえば「経験則」である。

・だが、帰納法には大きな欠点があり、それは導かれた性質は100%正しいとは限らないということだ。

・いちごの例でいうと、「(具体的な品種)は赤い」から「いちごは赤い」という結論を導いたが、実は白いいちごが存在するため「いちごは赤い」は数学的には偽である。

・これは
①具体例で白いいちごが挙げられていない
②結論の導き方に決まりはない
に起因される。

・次節で説明する数学的帰納法では、上の①、②のような曖昧さを取り除き、厳密な議論となっている。

２．数学的帰納法

2.1.イメージ

・下の例題を使って数学的帰納法を説明する。

・例題：すべての自然数$${n}$$に対し、$${n^3+2n}$$は3の倍数であることを示せ

・実際に$${n=1,n=2,n=3,n=4,n=5}$$の場合で考えると
$${n=1:1^3+2\cdot 1=1+2=3=3\cdot 1}$$
$${n=2:2^3+2\cdot 2=8+4=12=3\cdot 4}$$
$${n=3:3^3+2\cdot 3=27+6=33=3\cdot 11}$$
$${n=4:4^3+2\cdot 4=64+8=72=3\cdot 24}$$
$${n=5:5^3+2\cdot 5=125+10=135=3\cdot 45}$$
となり、すべての自然数$${n}$$においても成り立ちそうである。
・だが、$${n=1}$$~$${5}$$で成り立つからといってすべての自然数でも成り立つ！というのは数学的な証明ではない。（さきほどの「いちごは赤い」のような事態に陥りかねない）

・そこで無数にある自然数すべてで成り立つことを示すために、次のように考える。

Step1：$${n=1}$$の場合で成り立つことを示す。
Step2：自然数$${k}$$に対し、$${n=k}$$の場合で成り立つと仮定すると、$${n=k+1}$$の場合でも成り立つことを示す。

上のStep1,2から、どの自然数$${n}$$に対しても成り立つことが言える。

n=1でもn=100でもn=1億でも、Step1とStep2を使えば成立することが分かる

・もう少し具体的な例を考えよう。
・「すべての自然数$${n}$$に対し$${n^3+2n}$$は3の倍数である」を示したいとき、仮にStep1, Step2が成り立つことが分かれば、$${n=10}$$の場合で$${n^3+2n}$$は3の倍数であること（すなわち$${10^3+2\cdot 10}$$は3の倍数）が以下のようにして導かれる。

・まずStep1から、$${n=1}$$の場合で$${n^3+2n}$$は3の倍数になる
・次にStep2から、$${n=1+1=2}$$の場合でも$${n^3+2n}$$は3の倍数になる
・次にStep2から、$${n=2+1=3}$$の場合でも$${n^3+2n}$$は3の倍数になる
・次にStep2から、$${n=3+1=4}$$の場合でも$${n^3+2n}$$は3の倍数になる
・次にStep2から、$${n=4+1=5}$$の場合でも$${n^3+2n}$$は3の倍数になる
・次にStep2から、$${n=5+1=6}$$の場合でも$${n^3+2n}$$は3の倍数になる
・次にStep2から、$${n=6+1=7}$$の場合でも$${n^3+2n}$$は3の倍数になる
・次にStep2から、$${n=7+1=8}$$の場合でも$${n^3+2n}$$は3の倍数になる
・次にStep2から、$${n=8+1=9}$$の場合でも$${n^3+2n}$$は3の倍数になる
・最後にStep2から、$${n=9+1=10}$$の場合でも$${n^3+2n}$$は3の倍数になる

2.2.数学的帰納法の使い方

・2.2.節でも言ったように数学的帰納法とは「すべての自然数$${n}$$に対して～が成り立つ」という事実を、
（１）$${n=1}$$のとき～が成り立つ
（２）自然数$${k}$$に対し、$${n=k}$$で～が成り立つならば$${n=k+1}$$でも～が成り立つ
の２つを示すことによって証明を与える方法である。

・では2.1.節の例題のちゃんとした解法を下に述べる：
（例題の解法）
（１）$${n=1}$$のとき
$${1^3+2\cdot 1=1+2=3=3\cdot 1}$$で3の倍数となるため成立。
（２）自然数$${k}$$に対し$${n=k}$$で成り立つと仮定する。すなわち$${k^3+2k}$$が３の倍数であるとする。このとき、ある整数$${m}$$を用いて$${k^3+2k=3m}$$と表される。
$${n=k+1}$$のとき
$${(k+1)^3+2(k+1)=(k^3+2k)+(3k^2+3k+3)=3(m+k^2+k+1)}$$
となり、$${m+k^2+k+1}$$は整数なので$${3(m+k^2+k+1)}$$は3の倍数。以上から$${(k+1)^3+2(k+1)}$$は3の倍数。
（１）、（２）から、すべての自然数$${n}$$に対して$${n^3+2n}$$は３の倍数になることが分かった▢

・問題によって計算の過程や変数の置き方に多少の違いはあるが、大まかな流れ、書き方は上の解法のとおりである。

・実際にはこれの変則型がいくつかあるが、上級者向けであるということと、そういった問題に出くわす頻度はあまりないことから、この記事では扱わない。

（今回は演習問題なし）

以上