肩の荷(数字)を下ろす
昨日は数字の肩に乗った数字,指数についての話をした.今日はその肩の荷の話.
天文学が発達した頃,当時の科学者はとんでもなく面倒な計算に追われていた.天文学の計算では文字通りの天文学的な数字の掛け算や割り算,累乗を計算しなければならなかった.

例えばこんなのが(本当にあったとは思わないが)出てきたとして,電卓なしでこれがどれだけの数字なのかパッとイメージできる人はいるだろうか.いれば今日はこれでお別れだ.自身の暗算能力を誇って何かに生かして欲しい.
今日は暗算のやり方の話ではない.いくつかの数字を覚えて(表を作って)おけば上の計算も比較的簡単に,おおよその値を見積もることができるようになる話だ.その方法とは,指数の肩で話をすることなのだ.
------
突然だが,二つの正の数,"A"と"a"を用意してなんらかの数”x”を使えばこんな等式を成立させることができる.

指数の話から,xは実数全体をとるから,うまく"x"を決めればこうなるのだ.ということは,逆に二つの正数"A"と"a"を決めればxが決まる.このとき"x"がこう決まってますよ〜と言うために次のように書き直そう.

右辺は"ログa底(てい)A"と読む.これはまだ何も言ってない.ただ上の式を書き直す方法を決めただけだ."log"を対数と言う.また,"a"を対数の底(てい),"A"を真数(しんすう)という,ただの名前をつけただけだ.高校で指数と一緒にちょっと聞いたことがあるのではないだろうか.
まず対数がなんなのかもう一回言っておこう.対数とは指数の肩の数字を表す書き方なのだ."a"を”x”乗すれば"A"になりますよと言うことだ.
例えば
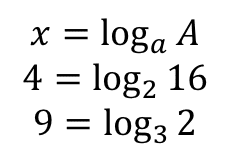
2の4乗は16だし,3の2乗は9だ.
対数は指数の肩を表すものだから,指数のときに見つけた加減乗除の法則が成り立つ.
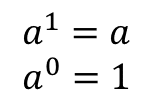
"a"は"a"の1乗だし,正の数を0乗したら1だから,

が言える.


累乗の積と商は指数の足し算と引き算になったから,

が言える.
また,何乗の何乗は指数の掛け算割り算になるから,


真数が何乗かされていれば,外に係数として出せる.

------
以下では対数の底は10にとる.これを常用対数と言う.10の何乗はそのもの桁数に繋がる.常用と言うだけに概算ではよく使えるのだ.
では先の問題に改めて取り掛かろう.対数を使うと扱う数字の桁数が劇的に小さくなって取り回しがしやすくなる.おもむろに対数を取り始める.
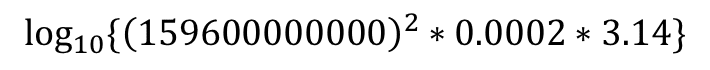
対数の定義に戻れば,これを最後に10の肩に乗せれば元の数になるのだ.まずは全ての数を1*10^(なんとか)乗にする.また,概算でいいので1596とか3.14はもう1600と3でいいと言うことにしてくれ.
それを認めて,先の法則を使って変形していく.

ここでおもむろに"常用対数表"なるものを持ってくる.この表はどうやって作んねんと言う問いかけには昔の人が頑張ったと答えておこう.実際問題,次の数だけ覚えておけばなんとかなることが多い.

そうすると先の変形を続けることができて,
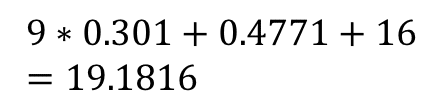
ここまでくれば元の数はこれを10の肩に乗せればいいのだ.10^0.1816ってのはなんやねんと言うのは,常用対数表を逆にみて,0.1816になる数字を探せば良い.だいたい1.5だ.
と言うことは

となって,15の後に0が18こ続く数になるのだ.真面目に計算するより明らかに扱う数字が小さくなっているのが見えると思う.
常用対数を使いこなせれば,2^2019とか3^123456789とかが何桁で初めの数がだいたいどれぐらいかがわかるようになる.
いいなと思ったら応援しよう!

