回る実:お話物理:場の量子論

今回から，ゲージ場と呼ばれる種類のベクトル場の構築をしていこうと思う．ゲージとはなんぞやという話はさておき，今日は複素数の話から始めよう．

複素数とは文字通り複数の素なる数を持った数で，言い換えれば二乗して正の数になる実数と，二乗して負の数になる虚数を合わせたものだ．虚数は虚数単位"i"と実数で書けて，結局複素数は，二つの実数の自由度をもつ数なのだ．

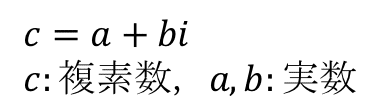
一つの数で実質二つの実数自由度を持つ複素数は，ある種の平面上の一点で表すことができる．

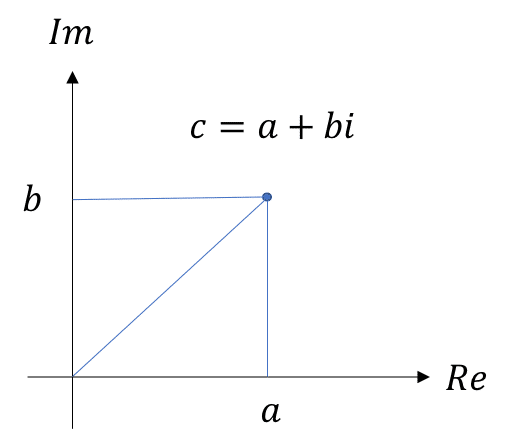
実軸:Reと虚軸:Imの値がそれぞれa，bであることがわかれば，複素数を一つ指定できる．

実数に対して，複素数は一つの数でもつ情報量が(ざっくり二倍)多く，お得な数だ．このことから実は自然は複素数でできている．

余談だが，僕には疑問がある．

物理の世界の理論は複素数を元に理論が構築されている．多くの変数やパラメタは一般に複素数が許されている．

しかし人間が観測できる量:物理量は実数しかない．この世に人間が感じられる数は実数しかない．この世は本来複素数でできているのにだ．

このねじれはどこから来るのか，それが疑問だ．"なぜ複素変数の理論の物理量は実数なのか"はいつか物理が答えなければならない問題だ．

閑話休題．

複素数が平面，二次元の情報量を持っているなら，そこには"回転"の自由度がある．言い換えれば，何を持って実数(虚数)というかの自由度がある．

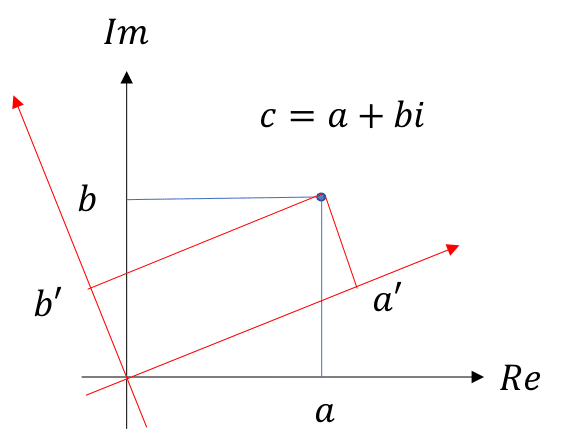
言い換えれば，見る人によって，何を実数にするかを変えて良いのだ．

物理の理論は，誰がみても同じ理論で書かれていなければならない．ゲージ場の理論は，ざっくり言うと，この複素数の回転の自由度に起因する理論だ．