お隣さんとのねじれ:お話物理:場の量子論

前回，複素回転に対してラグランジアンを不変にする理論を考えた．時空の各点で複素回転してもラグランジアンが不変になるように微分におまけを加えたのだった．

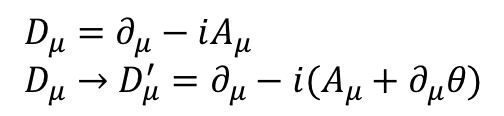
おまけであるベクトル"A"が複素回転と同時に変換することで，全体としてラグランジアンが不変に保たれるのだ．

ではこのベクトル場"A"は物理的にどう言う意味についてコメントしておこう．

もともと微分とは場の各点とその隣の点のつながりの効果を持ってくる項だ．

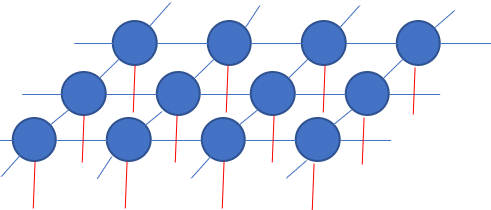
この青いバネに相当するのが微分項だ．

この微分が共変微分に変わったと言うことはバネの性質が変わったわけだ．"A"があると言うことは隣の場とのバネのつながりに手が加わっている．

今変わったのは，時空の各点で複素回転が起こったことだ．"A"は複素回転に対してラグランジアンを不変に保つように導入したのだから，"A"は時空の各点とその隣の点の複素回転のねじれを表している．ベクトルの脚"μ"があるのは当然，時空の各店のそれぞれの方向とのねじれを表しているのだ．

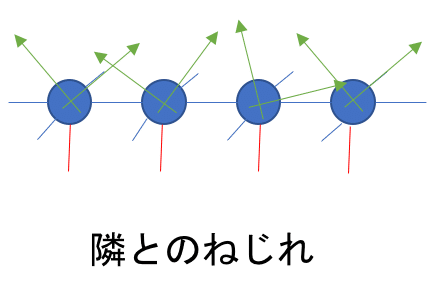
絵の緑が時空の各点での実軸(と虚軸)を表しているので"A_横"は隣同士の矢印のねじれに対応している．

時空の各点で実軸をどう取るかの自由度が与えられたが，そこで導入された"A"は要は，隣とのねじれ具合であり，言い換えれば時空の各点で実軸を実際どうとっているかと言う情報なのだ．