交わる粒子:お話物理:場の量子論

前回，場の理論に相互作用を導入した．相互作用は，場の高次の項によって導入されるものである．イメージとしては時空の各点の場に繋がっているバネの種類が(長さの三乗に比例する)特殊なバネが繋がったものになる．

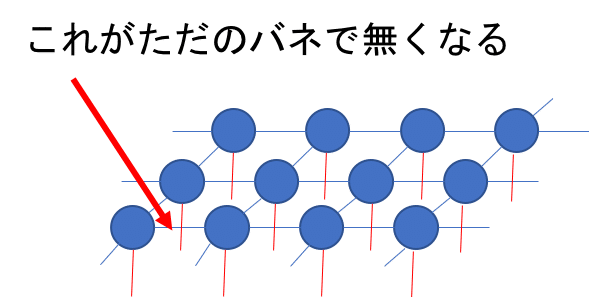
今回はこの"φ^4"項がなぜ相互作用と言うかについて話す．

今まで話してきた，自由場の理論は量子力学的にも，古典的にも，解としてただ直進する粒子が出てくる理論だった．

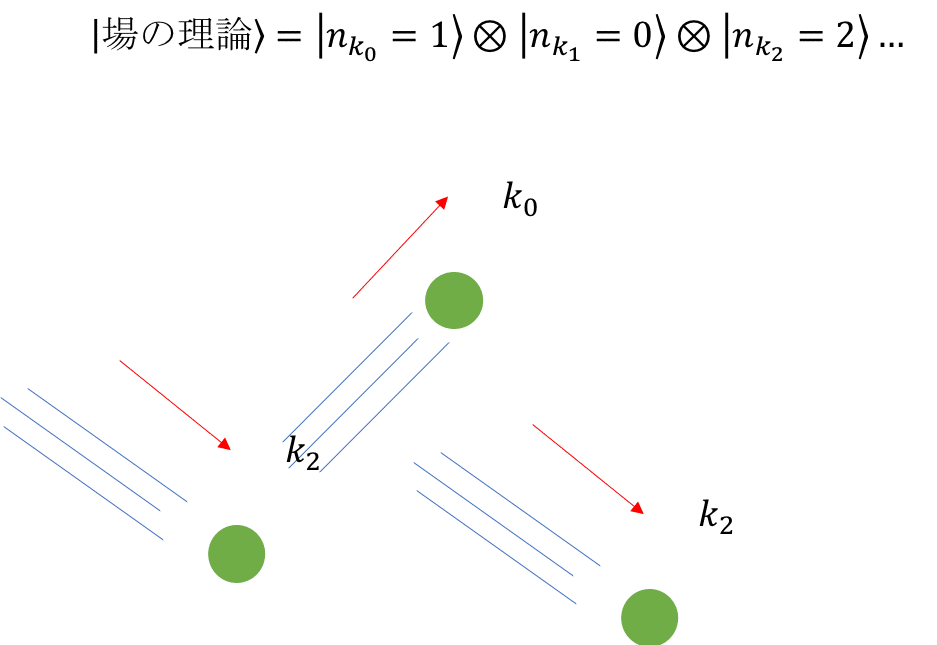
"ある運動量を持った粒子が何個"と指定してしまえば，状態が決まるのだった．

もし場の高次項があると，ラグランジアンから導かれる運動方程式が変化する．

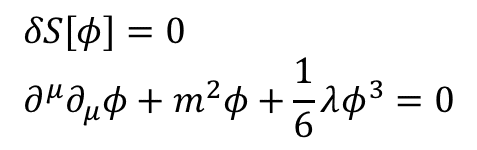
この"φ^3"の項が曲者なのだ．

なぜ曲者なのか．それは自由場でやった，フーリエ変換の意味での運動量のテクニックが使えなくなるのだ(微分方程式の言葉で言えば線型性がないことが曲者だ)．

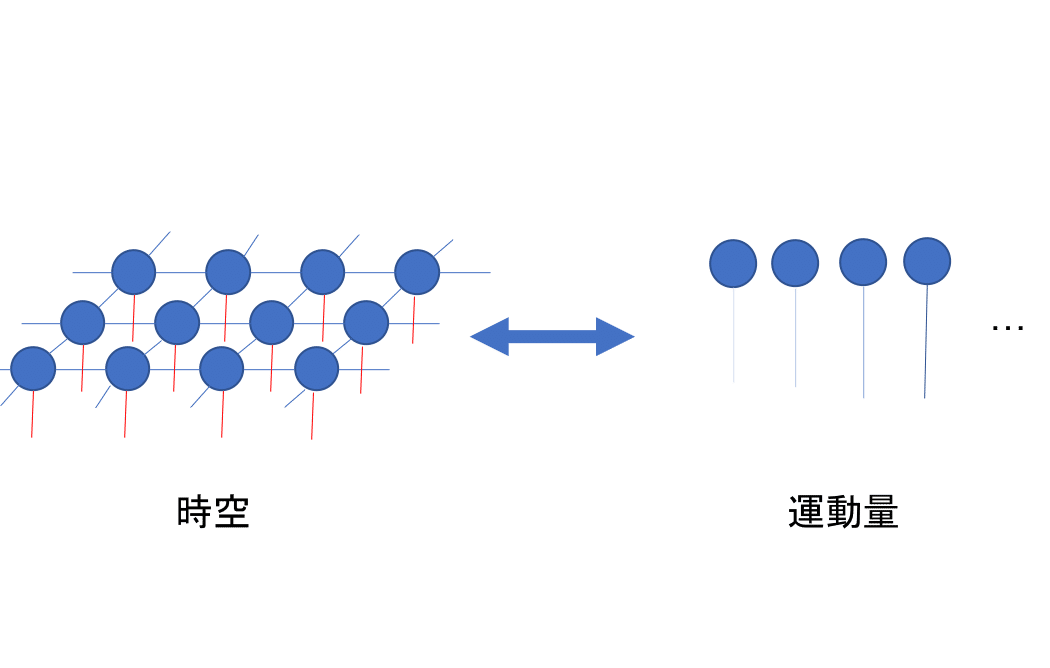
運動量で見ることで，時空の隣同士に繋がったバネ(~微分)が分離できて運動量の種類だけ無限個ある独立なバネの問題に取り替えることができたのだった．

しかし微分方程式が線型性を失ったことでこの運動量の世界にいってもバネが独立なものに見直せなくなってしまうのだ．言い換えれば，今まで解けていた微分方程式が解けなくなってしまうのだ．

イメージとしては運動量空間で見たバネ同士が繋がっているのだ．

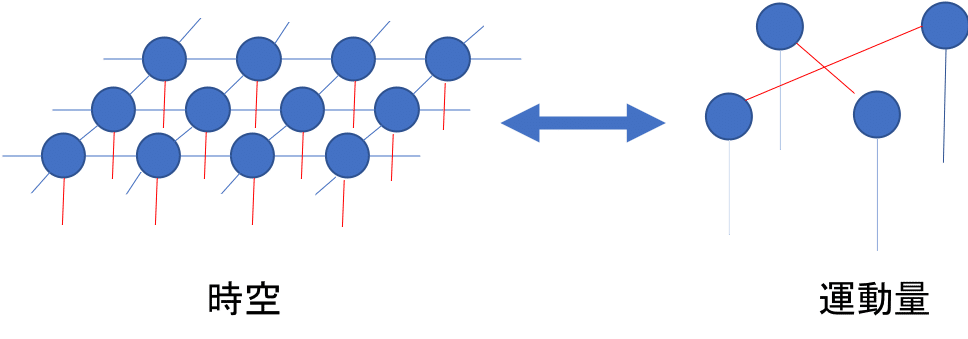
分離できてしまったバネがまた繋がってしまった．それがコトを難しくする原因で，しかもそれが相互作用であるのだ．

この運動量で見たバネ同士の繋がりがなぜ相互作用と言うか．それは運動量のバネ同士の繋がりによって粒子の運動量を取り替えることができるのだ．

そもそも相互作用とは，複数のものが影響を及ぼしあうことだ．粒子の相互作用に限れば，ぶつかり跳ね返ることをイメージすれば簡単だろう．

粒子が二つあって，何らかの"相互作用"が起こるなら，粒子の運動量(~進む向き)が変わる．つまり運動量が変わるのだ．

この粒子の運動量が変わることが，運動量で見たバネ同士の繋がりによって実現できるのだ．

運動量空間のバネの振動(を量子化したもの)が粒子なのだから，振動するバネが変われば，それは粒子の運動量が変わったことを意味する．

この運動量の交換は，相互作用項の導入によって実現するのだ．