粒々の波になりたい:お話物理:場の量子論

前回は自由粒子の古典解を得たのだった．

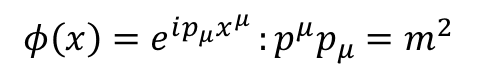
ある運動量の解が上のような場で再現されるのだった．そして粒子の質量"m"は場の理論のラグランジアンの場の二乗項の係数で決まるのだった．

ただ，この場の解は指数関数の形になっている．指数関数(の複素数乗は)ただの波になる．つまり古典的には場の理論の解は粒子描像などなく，ただの波なのだ．

ん，場の理論はそもそもなんで考え始めたのだったか？それは粒子の生まれ消えるような量子力学を記述するために考え始めたのだ．

と言うことは場の理論の粒子描像を得るためには，場の量子論に行かねばならないのだ．

我々がお話でやってきた量子化は"経路積分量子化"と言うものだった．

古典的には運動方程式は作用の最小化と動議だ．古典的に実現する解は，"作用"と呼ばれるものを最小化する経路がそのまま選ばれるのだった．

しかし量子力学では，この世の全ての経路がその経路で決まる作用の重みの分だけ確率的に起こるのだった．

詳しくは上を読んでくれ．

さて今回も経路積分量子化をすると場の量子論になるのだが，それでは粒子描像がわかりにくい形になってしまう．

それで次回から経路積分量子化とは別の(全く同義の)量子化，正準量子化の話をしようと思う．

-------

お話物理では僕の個人の思想はもりもりだが，体調や気分に関しては関知しないようにしてきた．

今後もそうするつもりだが，質と量にばらつきが出てしまう気がする．

まぁ明け方の更新を辞めて，日中に書けばもっとましになるだろう．もしお話物理を読んでいる偏屈な人がいるなら，これ以上に気長に待ってほしい．