飛び散り方:お話物理:摂動論

前回までのお話物理で，散乱を記述するS行列をなんとか人間が計算する為に，摂動展開と言う，近似計算を始めたのだった．

散乱問題の摂動計算として，自由粒子がポテンシャル"V"の摂動を受ける状況を考えたのだった．

青の部分はVの影響を受けずそのまま素通りする部分，赤の部分がVの影響を一回受けて散乱される，最低次の部分だ．

今回は電子-陽子散乱の具体的なハミルトニアン

で摂動の最低次がどうなるか，計算してみよう．

陽子の作るポテンシャルの影響を受けて散乱される電子はS行列要素

の計算を実行する．

真面目に考えなければならない部分は二つ．一つは時間積分の部分と，もう一つは運動量固有状態の行列要素の部分だ．

行列要素の部分は時間に依らないから，時間積分の部分とそれぞれ考えることができて，

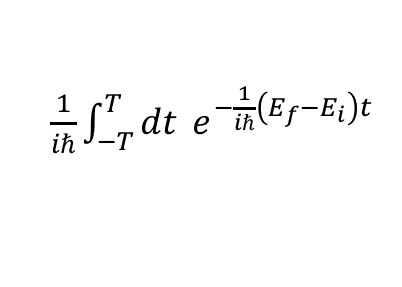
と

を実行すればいいのだ．

まずは時間積分から考えよう．指数関数の積分はビームの打ち出しから出てくるまでの時間"T"がものすごく長いことを使うと"デルタ関数"と呼ばれるものになる．

デルタ関数は，物理屋さんが使う便利な関数で，積分を前提にした関数だ．

x=0以外ではδ(x)=0で，x=0でのみ値:むをもつ．特殊な関数だ．

デルタ関数と言うのは中々やばい関数で，数学的にきっちり議論してから使うべきなのだが，物理屋さんはガバガバなまま使うし，ここはお話物理，デルタ関数を使う気持ちだけ話しておこう．

"δ(E_i-E_f)"という形になっている訳だから，"E_i=E_f"以外でS行列要素が値を持たない，つまり始状態と終状態のエネルギーが違う場合，遷移確率が0であると言うことだ．

もうちょっとはっきり言えば，始状態と終状態のエネルギーが同じにならなければならない．つまりエネルギーが保存する必要がある．

余談

でもデルタ関数は積分を前提にした関数と言っていたではないか．S行列要素のどこに(エネルギー)積分があるのか．

確かに見かけ上はエネルギー積分はない．しかし現実の状況を考えるに，ビームの打ち出しのエネルギーを完全に揃えることも，検出時に無限の精度で粒子のエネルギーを測定することはできない．ある程度の幅を持ったエネルギーを測定することになる．この幅をまとめて考えることが積分を暗にやっていることになる．

そうやって物理屋はデルタ関数について言い訳をしておく．余談終わり．

時間積分の部分は人間が測定をできる範囲では"エネルギーが保存する"と言う条件を生み出す．この条件は，ポテンシャルが時間に依らない場合の一般に成り立つ．

では運動量固有状態の行列要素はどうなるのか．

ブラケット"<p_f|V|p_i>"で書かれたものは，成分が無限個あるベクトルの内積だった．成分無限のベクトルなど人間には計算できない．

しかしこれの計算には，量子力学の完全系

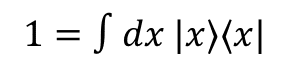
を入れれば波動関数の形で計算できる．

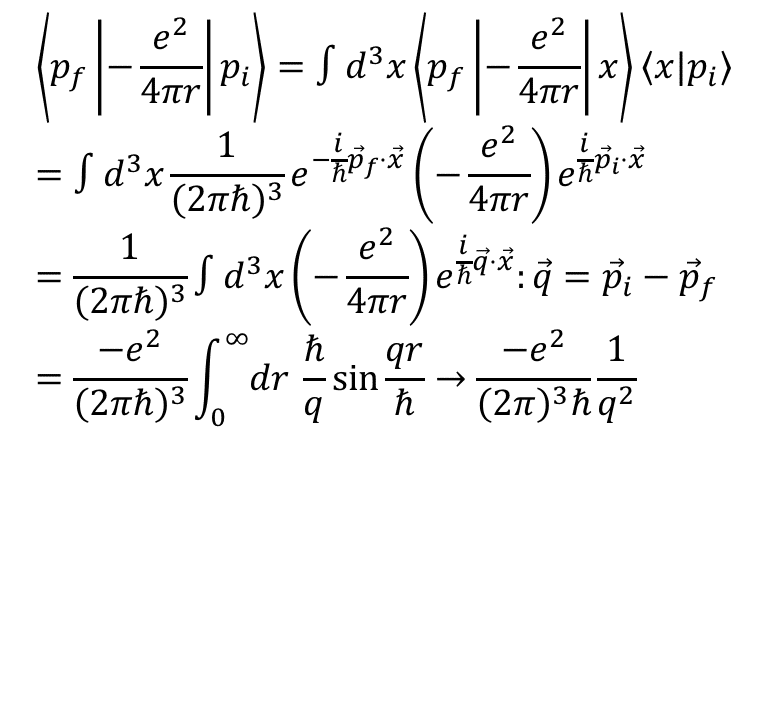
最後の"r"積分の上端は∞になって値が収束しないのだが，適切な(境界)条件を課すことで0になる．ざっくり言うと散乱された粒子が"出てくる"と言う条件だ．

まとめると

おぉ，なんか計算できた．θはビームの散乱角だ．あとはこれを二乗すれば，ある運動量"p_f"への遷移確率になる．ビームの単位時間，単位立体角(dΩ:ある方向)あたりの散乱を考えると，

になる．これを微分散乱断面積と言う．

最後の最後に計算が面倒になってすっ飛ばしてしまった．まぁ誰も計算を追う気はないだろうから許してほしい．

計算はさておき，ビームの散乱される角度によってその確率が変わると言うことだ．

実験ではこの角度によってどう言う飛び散り方をするかで，その粒子同士の相互作用を調べることになる．

例えばこの場合，ポテンシャル"V"が電子と陽子の相互作用を司っていた．実験で先のような微分散乱断面積が測定できれば，このポテンシャルで相互作用していたのだなと検証できるのだ．

逆に理論計算を実験結果がずれていれば，相互作用がこのポテンシャルではないと，修正が必要になる．