スクリーンショット_2019-04-22_19

移行しやすいルール探し 遺伝セルオートマトン Genelife Part 3

おちゃちゃ

今日の Genelife は、ルールの関係を調査する話です。

まず、これまで作っていたものについて、想定どおりの挙動でなかった所謂バグを退治したのと、ルールの表記方法を簡単にできるような修正をしました。

今まではこのようなビット列でルールを設定していました。

これだとルールを作るのもめんどくさい、ということでこのビット列を一般的なルール記法から作るプログラムを作りました。

この 01234567/3/8 みたいな表記が8近傍総和型世代セルオートマトンの記法になります。出処はわかりませんが、おそらく MCell の作者 Mirek Wojtowicz さんです。

この表記の変換コードはとてもシンプルで、このようになっています。

std::uint64_t Rule::rule_str_to_bits(const std::string &str) const {
 std::uint64_t dest = 0;
 int mode = 0;
 for (int i = 0; i < str.length(); i++) {
   auto s = str[i];
   if (s == '/') {
     mode++;
     continue;
   }
   char ss[3] = "";
   sprintf(ss, "%c", s);
   int a = std::atoi(ss);
   if (mode == 0) {
     dest |=
         0b00000000'00000000'10000000'00000000'00000000'00000000'00000000'00000000 >>
         a;
   }
   if (mode == 1) {
     dest |=
         0b10000000'00000000'00000000'00000000'00000000'00000000'00000000'00000000 >>
         a;
   }
   if (mode == 2) {
     dest |= (((std::uint64_t)(a)-2) << ((8 * 6)));
   }
 }
 return dest;
}

ビット演算系のコードを書くことなんて、仕事やゲーム制作では最近だとシェーダーを作るときに出てくることがあるくらいで、他はほとんどなくなってしまいましたが、改めて触ってみるとビット列って便利ですね。

ということで、話を戻しますが、改めて今どのようなルールでこの Genelife が動作しているか説明します。

現在の Genelife の仕組み

今の Genelife は、予め用意された複数のルールが組み合わさって動いています。

一般的な2次元セルオートマトンとの違いとして説明します。

ある生きているセルは、自分自身が持つルールに従って近傍8セルの総和に基づき自分が次にどの状態に遷移するかが決定されます。

次に死んでいるセルはルールを持っていません。そのため近傍8セルのうちランダムなセルのルールを採用し、自分自身の次の状態を決定します。

このとき、死んでいるセルは生きるときに近傍8セルのうち生きているセルの年齢の最も高齢のものを引き継ぎ、1つ歳をとります。つまり、セルが誕生するときは年齢が周囲より1つ増えているということです。年齢と言っていますが、私達の概念の正確な意味を表していません。

次に、年齢が決められた年齢になったとき、自身のもつルールが変更されます。これは年代ごとに決められています。例えば 0〜99 歳はルール A、100〜199 歳はルール B といった具合です。現状は年代幅は100に固定されています。

これが仕組みとなります。

それでは、今この仕組みで何を行っているか、ということを説明します。

Genelife のルール間の移行しやすさ

あるルールと別のルールの間には、その移り変わりやすさというものがあります。これは年代が変化したときに次のルールに定着しやすいか、ということを意味します。例えを動画にしています。

この動画は、Meteor Guns というルールが Starwars ルールへ移行しやすいことを示しています。最初のごちゃごちゃもぞもぞしているものが Meteor Guns というルールでできたセル群で、そこから濃い青のものが何度か射出されていますが、この濃い青が Starwars ルールのセル群です。

このようにルールが次のルールに移行しやすいかどうかを、マイグレータビリティ（Migratability）と言うことにします。そして、今回はこのマイグレータビリティの度合いの調査手法の1つを発見したのでそれを紹介します。

なおマイグレータビリティの高さはルール同士の関係の強さでもあるので、マイグレート順を決定するときに非常に便利な指標となります。

マイグレータビリティの調査手法 Gnarl ルールを用いた方法

Gnarl ルールというものがあります。動画で表すとこのようなルールです。

このルールは1ステップごとに必ず1つ隣のセルにルールを移動すること、そして2ステップ以上に渡ってセルが生き続けることは一部の例外を除いて発生しない、また殆どのルールから移行しやすい（マイグレータブル）だという特徴を持っています。

これがどんな効果をもたらすか、というと、一旦このルールに移行したとき、空間全体をできる限り Gnarl ルールで埋め尽くします。そして Gnarl は必ず1ステップごとに歳をとるので一定時間後に次のルールに移行します。移行する直前の Gnarl の状態は適度な密度を持っており、Gnarl から移行してきた新しいルールは、その密度により新たなルールが定着しやすい、つまりマイグレータビリティが高いということになります。

これは非常に強力です。実際に試してみた動画がこちらです。

これは Gnarl と High Life の2種類だけが予め設定されているルールで、100ステップごとに Gnarl が画面全体に飽和し、その100ステップ後に High Life に移行でき、定着しなかった場所ではセルが消滅する、ということを繰り返しています。

これを例えるなら定期的な掃除屋です。画面全体を覆い隠すようにいろいろなものを飲み込んでしまうので、リセットの役割を持っています（一部それに影響されない守られた場所もありますが）。High Life は Gnarl へのマイグレータビリティが高いのでリセット後に High Life が戻ってきます。また Gnarl がある程度の空間を生み出してくれています。では一旦、このループを前提に考えてみます。

この High Life -> Gnarl -> High Life -> Gnarl のループを High Life -> ルールA -> Gnarl -> High Life と別のルールを差し込んでみるとどうなるのでしょうか？これはつまり High Life からのマイグレータビリティが高いルールAは何か、ということを評価することができることになります。
Gnarl は High Life に必ず移行しますが、High Life から ルールAに移行できなかった場合は Gnarl も発生しません。つまりループが途絶えることになります。
何度も Gnarl が発生することはルールAが High Life からの優れたマイグレータビリティを持っていることを意味します。

マイグレータビリティの高いルールAをいろいろ探してみる

ルールAは何でも良いわけですが、ルールというのも五万とあるので、どのルールが優れているか探すのは一苦労です。一旦、適当に試してみましょう。

これはルールAに先程使った Meteor Guns を採用してみた例です。しばらく見ていると完全にクラスIもしくはクラスII状態になりました。クラスIIというのは Wikipedia のこのページを御覧ください。

クラスI とIIは停滞状態であり、Gnarl にもならずこれ以上変化のない状態となりました。つまり、High Life -> Meteor Guns のマイグレータビリティはとても低いといえます。何度試してもこの状態になります。

他のルールについても同じような現象が多発しています。例えば Starwars ルールへのマイグレータビリティも多分0です。これは機械的に計測可能です。

その方法はとても簡単です。一定時間 Gnarl ルールが発生しない状態が続いたら、マイグレートに失敗しているということを示せます。その時間の長さがどれくらいだったかがマイグレータビリティとイコールになります。これは何度か繰り返して平均と取ったものをマイグレータビリティにする、というわけです。

なので、この方法をルールAを入れ替えながら何度も評価すると High Life からルールAに対してのマイグレータビリティを定量的に評価できることになります。しかも、重要なこととしてルールAはランダムで生成できるので、世の中のすべてのルールに対して High Life からのマイグレータビリティが計測できることになります。

High Life 以外からのマイグレータビリティについて（そして Gnarl の安定化現象の謎）

では、High Life 以外からのマイグレータビリティの評価も可能なのだろうか？という疑問が出てきます。Gnarl は他のルールへのマイグレータビリティが高いと考えられるので、試しに Starwars と Gnarl の関係を評価してみました。すると、実は不思議な停滞状態になってしまいました。

すごく複雑な状態で停滞しました。それは次の画像のような状態です。

実はこの状態は、Starwars もしくは Gnarl のどちらか単体だけでは決して維持できない状態です。つまり混在しています。Gnarl でできた安定状態の核に Starwars による不思議な周期的な波が覆っている個体で満たされています。殆ど起こりえない Gnarl の安定です。Gnarl がなぜか安定しており Gnarl だけではありえない安定の仕方です。

ルールを視覚化するとこうなります。

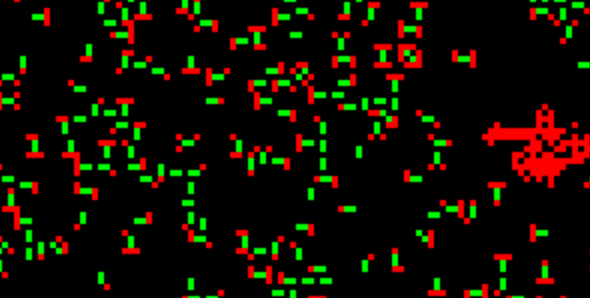
緑が核となっているドミノ型（縦1横2セル・もしくは横1縦2セル）の Gnarl で、赤が Starwars です。Gnarl の核の周りにまとわりつくことができるルールが存在すると、Gnarl はこのドミノ型で安定するようです。

こうなると、Gnarl は Starwars に対してはマイグレータビリティが低いだけでなく、組み合わさった特殊な状態になりやすいことがわかります。しかしこの特殊な状態を定量的に計測する方法は今の所思いつきません。ただ、複数のルールが組み合わさってできる個体や現象は、Genelife で探したいものですからこの発見はとても喜ばしいことだったりします。

実はこの状態は他のルールでもよく発生しています。Starwars 以外だと Sticks(3456/2/6) や Worms(3467/25/6) といったルールでも同じ現象が発生しています。

Gnarl が安定してしまうと次の Gnarl ウェーブが発生しないため、停滞状態に陥ります。この安定状態がどのようなメカニズムで発生しているかは、だいたいわかっていますが、今回はあまり踏み込んだ話は割愛します。が、推測から導き出したオリジナルルール(345/2345/3)で Gnarl 核をまとって安定させることに成功しました。より大きな Gnarl 核を作ることができています。

High Life からのマイグレータビリティ計測の実装について

まだマイグレータビリティ計測ツールは実装していません。次はそれを実装してみようと考えています。しかし High Life が挟まっていない場合は Gnarl が安定してしまうことがあるため、Gnarl が一定時間発生しなければ、という評価基準においてマイグレータビリティが無限に高いことになってしまいます。少し工夫が必要というわけです。一旦は High Life からのマイグレータビリティだけを考えますが、すぐに他のルールとの関係性を評価する仕組みが必要になってしまうでしょう。

解決策は Gnarl 以外のルールを探すか、Gnarl を一定時間で消滅させる神始点のルールを追加するとか、Gnarl が安定しても数の変動がなければ発生していないとする、といった方法が考えられるので、やりようは結構残されています。

それでは。

いいなと思ったら応援しよう！

おちゃちゃ
応援してくださると嬉しいです。よろしくお願いいたします！