『Python実践データ分析100本ノック』ノック55〜60

今回は、『Python実践データ分析100本ノック』で学んだことをアウトプットします。

ノック５５：ルートの重みづけを実施しよう

ノード（頂点）間のリンクの太さを変えていく（重みづけを行う）ことで、物流の最適ルートをわかりやすく可視化していくことができるようになります。

ここでは、CSVファイルに格納された重み情報をデータフレーム形式で読み込み、その数値を使って重みづけすることにします。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

# データ読み込み
df_w = pd.read_csv('network_weight.csv')
df_p = pd.read_csv('network_pos.csv')

# エッジの重みのリスト化
size = 10
edge_weights = []
for i in range(len(df_w)):
   for j in range(len(df_w.columns)):
       edge_weights.append(df_w.iloc[i][j] * size)
       
# グラフオブジェクトの作成
G = nx.Graph()

# 頂点の設定
for i in range(len(df_w.columns)):
   G.add_node(df_w.columns[i])

# 辺の設定
for i in range(len(df_w.columns)):
   for j in range(len(df_w.columns)):
       G.add_edge(df_w.columns[i], df_w.columns[j])
       
# 座標の設定
pos = {}
for i in range(len(df_w.columns)):
   node = df_w.columns[i]
   pos[node] = [df_p[node][0], df_p[node][1]]
   
# 描画
nx.draw(G, pos, with_labels=True, font_size=16, node_size=1000, node_color='k', font_color='w', width=edge_weights)

# 表示
plt.show()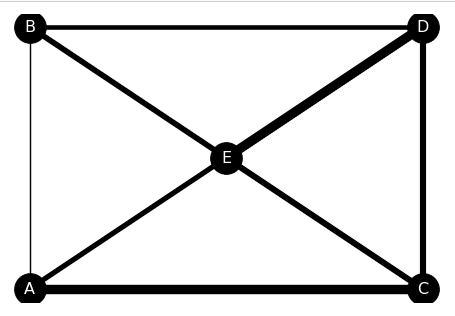

まず、pandasを用いて、CSV形式のリンクごとの重みを記載したファイルnetwork_weight.csvと、各リンクの位置を記載したファイルnetwork_pos.csvをデータフレーム形式で読み込みます。

次に、リンクの重みをリスト形式で格納し直していきます。このリンクの重みリストの順番は、後で登録する辺（リンク）の設定の順番と一致させる必要があります。

その次に、グラフオブジェクトを宣言し、頂点とそれをつなぐ辺、そして頂点の位置のそれぞれを、データフレームから読み込むことで設定します。

関数drawによる描画では、フォントサイズ、ノードサイズ、ノードの色、フォントの色を引数によって指定しています。

引数の最後に、widthとして先ほど作成したリンクの重みリストを与えることによって、重み付けしたリンクを描画することができます。

ノック57：輸送ルート情報からネットワークを可視化してみよう

現状、どの倉庫からその工場へ、どれだけの量の輸送が行われているのかを記録したファイルtrans_route.csvから、ネットワークの可視化を行ってみます。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

# データの読み込み
df_tr = pd.read_csv('trans_route.csv', index_col='工場')
df_pos = pd.read_csv('trans_route_pos.csv')
       
# グラフオブジェクトの作成
G = nx.Graph()

# 頂点の設定
for i in range(len(df_pos.columns)):
   G.add_node(df_pos.columns[i])
   
# 辺の設定&エッジの重みのリスト化
num_pre = 0
edge_weights = []
size = 0.1
for i in range(len(df_pos.columns)):
   for j in range(len(df_pos.columns)):
       if not (i == j):
           # 辺の追加
           G.add_edge(df_pos.columns[i], df_pos.columns[j])
           # エッジの重みの追加
           if num_pre < len(G.edges):
               num_pre = len(G.edges)
               weight = 0
               if (df_pos.columns[i] in df_tr.columns) and (df_pos.columns[j] in df_tr.index):
                   if df_tr[df_pos.columns[i]][df_pos.columns[j]]:
                       weight = df_tr[df_pos.columns[i]][df_pos.colunms[j]] * size
               elif (df_pos.columns[j] in df_tr.columns) and (df_pos.columns[i] in df_tr.index):
                   if df_tr[df_pos.columns[j]][df_pos.columns[i]]:
                       weight = df_tr[df_pos.columns[j]][df_pos.columns[i]] * size
               edge_weights.append(weight)
               
# 座標の設定
pos = {}
for i in range(len(df_pos.columns)):
   node = df_pos.columns[i]
   pos[node] = (df_pos[node][0], df_pos[node][1])
   
# 描画
nx.draw(G, pos, with_labels=True, font_size=16, node_size = 1000, node_color = 'k', font_color='w', width=edge_weights)

# 表示
plt.show()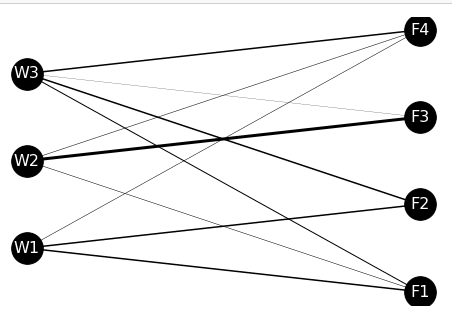

輸送ルート情報に加え、倉庫と工場を頂点として表現するために、それらを表示するための位置情報を格納したtrans_route_pos.csvを作成し、読み込みます。

左側に倉庫W1, W2, W3が、右側に工場F1, F2, F3,F4が並ぶようにすると、全体像を把握しやすくなります。

次に、グラフオブジェクトの宣言を行い、頂点を設定します。頂点情報は、位置情報を含めて記載しているtrans_route_pos.csvを用いると作りやすいです。

そして、辺の設定と、エッジの重みリストの作成を同時に行います。こうすることで、辺の数と、エッジの重みの数がずれなくなります。

そして、読み込んだ頂点の位置情報をposに格納した上で、描画を行います。描画したネットワークを見ると、どの倉庫とどの工場の間に多くの輸送が行われているかが分かります。

ノック58：輸送コスト関数を作成しよう

ノック57を通して輸送ルートを可視化することで、「改善の余地が見込めるかもしれない」という感覚的な仮設を立てることができました。実際に改善を行うためには、輸送最適化問題を解く必要があります。

「最適化問題」と解くためには、まず、最小化（または最大化）したいものを関数として定義します。これを「目的関数」と呼びます。

次に、最小化（または最大化）を行うにあたって、守るべき条件を定義します。これを「制約条件」と呼びます。

考えられるあらゆる輸送ルートの組み合わせの中から、制約条件を満たした上で目的関数を最小化（または最大化）する組み合わせを選択する、というのが、最適化問題の大きな流れです。

まず、輸送コストを計算する関数を作成し、それを目的関数とします。輸送ルート情報trans_route.csvと、各輸送ルートに必要なコストを記載したtranc_cost.csvから、輸送コストを計算する関数を作成してみます。

import pandas as pd

# データ読み込み
df_tr = pd.read_csv('trans_route.csv', index_col='工場')
df_tc = pd.read_csv('trans_cost.csv', index_col='工場')

# 輸送コスト関数
def trans_cost(df_tr, df_tc):
   cost = 0
   for i in range(len(df_tc.index)):
       for j in range(len(df_tr.columns)):
           cost += df_tr.iloc[i][j] * df_tc.iloc[i][j]
   return cost

print('総輸送コスト：'+ str(trans_cost(df_tr, df_tc)))

今回の輸送コストは、ある輸送ルートの輸送量とコストを掛け合わせ、それらをすべて足し合わせることで算出できます。

この関数を作成しておくことで、変更後のルートでの輸送コストを計算でき、現在のルートとの比較がしやすくなります。

現在の輸送コストは1493（万円）でした。数%でも輸送コストが削減できれば、大きなコスト削減に繋がります。

ノック59：制約条件を作ってみよう

今度は、ノック58で作成した輸送コスト関数を最適化していく上での制約条件について考えていきましょう。各倉庫には供給可能な部品数の上限があり、また、各工場には、満たすべき最低限の製品製造量があります。

それぞれを格納したsupply.csvおよびdemand.csvを読み込んだ上で、制約条件を満たすかどうかを確認していきます。

import pandas as pd

# データ読み込み
df_tr = pd.read_csv('trans_route.csv', index_col='工場')
df_demand = pd.read_csv('demand.csv')
df_supply = pd.read_csv('supply.csv')

# 需要側の制約条件
for i in range(len(df_demand.columns)):
   temp_sum = sum(df_tr[df_demand.columns[i]])
   print(str(df_demand.columns[i]) + 'への輸送量：' + str(temp_sum) + ' (需要量：' + str(df_demand.iloc[0][i])+')')
   if temp_sum >= df_demand.iloc[0][i]:
         print('需要量を満たしています。')
   else:
         print('需要量を満たしていません。輸送ルートを再計算してください。')
         
# 供給側の制約条件
for i in range(len(df_supply.columns)):
   temp_sum = sum(df_tr.loc[df_supply.columns[i]])
   print(str(df_supply.columns[i])+ 'からの輸送量：' + str(temp_sum)+ '(供給限界：' + str(df_supply.iloc[0][i])+')')
   if temp_sum <= df_supply.iloc[0][i]:
       print('供給限界の範囲内です。')
   else:
       print('供給限界を超過しています。輸送ルートを再計算してください。')

まず、工場で製造される製品の数が需要量を満たすかどうかは、各工場に運び込まれる製品の数と、各工場に対する需要量を比較することで検討可能であり、それがそのまま制約条件になります。

同様に、倉庫から工場に出荷される部品の数が、各倉庫の供給限界を超えるかどうかは、各倉庫から出荷される部品の数と、各倉庫の供給限界とを比較することで検討可能です。

if文によって確認することで、現状の輸送ルートは、制約条件を満たしていることが分かります。この制約条件を作っておくことで、輸送ルートを変更した後に、新しいルートが制約条件を満たすかどうかを確認できます。

ノック60：輸送ルートを変更して、輸送コストの変化を確認しよう

trans_route_new.csvに記載された、試しに変更してみたルートが、制約条件を満たしているかどうか、そしてどの程度のコスト改善が見込めるのかを計算してみます。

import pandas as pd
import numpy as np

# データの読み込み
df_tr_new = pd.read_csv('trans_route_new.csv', index_col='工場')
print(df_tr_new)

# 総輸送コスト再計算
print('総輸送コスト（変更後)：' + str(trans_cost(df_tr_new, df_tc)))

# 制約条件計算関数
def condition_demand(df_tr, df_demand):
   flag = np.zeros(len(df_demand.columns))
   for i in range(len(df_demand.columns)):
       temp_sum = sum(df_tr[df_demand.columns[i]])
       if (temp_sum >= df_demand.iloc[0][i]):
           flag[i] = 1
   return flag

# 供給側
def condition_supply(df_tr, df_supply):
   flag = np.zeros(len(df_supply.columns))
   for i in range(len(df_supply.columns)):
       temp_sum = sum(df_tr.loc[df_supply.columns[i]])
       if temp_sum <= df_supply.iloc[0][i]:
           flag[i] = 1
   return flag

print('需要条件計算結果：' +str(condition_demand(df_tr_new, df_demand)))
print('供給条件結果：' + str(condition_supply(df_tr_new, df_supply)))

まず、輸送コストは、ノック58で作成した関数trans_costを用いれば、すぐに計算することができます。

次に、制約条件は、ノック59で作ったif文による判断結果をフラグ化しておく（条件を満たす場合は1を、そうでない場合は0を表記する）ことで、各制約条件をみたせているかどうかを確認できます。

今回、読み込んだルートは、W1からF4への輸送を減らし、その分をW2からF4への輸送で補う、というものです。

これによる輸送コストは1418（万円）であり、もとの輸送コスト1493（万縁）に比べて若干のコストカットは見込めそうです。

しかしながら、二番目の供給条件が満たせておらず、工場W2からの供給限界を超えてしまっていることが分かります。