
Photo by
ibaraki_nakai
『Python実践データ分析100本ノック』ノック65〜67
今回は、『Python実践データ分析100本ノック』で学んだことをアウトプットしていきます。
ノック65:利益を計算する関数を作ってみよう
生産計画の最適化(すなわち生産最適化)の解き方もまた、最適化問題の一般的な流れと同じです。
すなわち、まず、目的関数と制約条件を定義し、制約条件化で目的関数を最小化(または最大化)する変数の組み合わせを探し出します。
まずは、利益を計算する関数を作り、これを目的関数として最大化することを検討していきます。
def product_plan(df_profit, df_plan):
profit = 0
for i in range(len(df_profit.columns)):
for j in range(len(df_plan.columns)):
profit += df_profit.iloc[i][j] * df_plan.iloc[i][j]
return profit
print('総利益:' +str(product_plan(df_profit, df_plan)))生産計画の総利益は、各製品の利益と製造料との積の和によって計算できます。
ノック66:生産最適化問題を解いてみよう
ノック61と同じ流れで、先ほど定式化した目的関数である利益関数を最大化することを目的とし、最適化計算を実施してみます。
import pandas as pd
from pulp import LpVariable, lpSum, value
from ortoolpy import model_max, addvars, addvals
m = model_max()
v1 = {(i):LpVariable('v%d'%(i), lowBound=0) for i in range(len(df_profit))}
m += lpSum(df_profit.iloc[i]*v1[i] for i in range(len(df_profit)))
for i in range(len(df_material.columns)):
m += lpSum(df_material.iloc[j, i] * v1[j] for j in range(len(df_profit))) <= df_stock.iloc[:, i]
m.solve()
df_plan_sol = df_plan.copy()
for k, x in v1.items():
df_plan_sol.iloc[k] = value(x)
print(df_plan_sol)
print('総利益:' + str(value(m.objective)))
ノック67:最適生産計画が制約条件内に収まっているかどうかを確認しよう
制約条件で規定した、「それぞれの原材料の使用量」がどの程度であり、それが「在庫を効率よく利用できているか」を調べてみます。
def condition_stock(df_plan, df_material, df_stock):
flag = np.zeros(len(df_material.columns))
for i in range(len(df_material.columns)):
temp_sum = 0
for j in range(len(df_material.index)):
temp_sum = temp_sum + df_material.iloc[j][i] * float(df_plan.iloc[j])
if (temp_sum <= float(df_stock.iloc[0][i])):
flag[i] = 1
print(df_material.columns[i] + ' 使用量:' + str(temp_sum) + ' 在庫:' + str(float(df_stock.iloc[0][i])))
return flag
print('制約条件計算結果:' + str(condition_stock(df_plan_sol, df_material, df_stock)))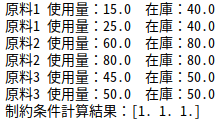
制約条件はすべて満たされており、そのうえで、原料2と原料3に関しては、在庫をすべて利用できています。原料1が少し余っていますが、最適化計算以前と比べると、原料の利用効率が大きく改善できていることが分かります。
サポート、本当にありがとうございます。サポートしていただいた金額は、知的サイドハッスルとして取り組んでいる、個人研究の費用に充てさせていただきますね♪
