#37　マイナス投入方式の場合、重量単価が副産物が投入される産業のものになる

#36にて、マイナス投入方式を列方向でみた場合と、行方向でみた場合とで考察を試みました。

まず、産業連関表を列方向でみた場合を考えます。石油化学産業の列に注目した場合、石油化学産業で副産物として生産されたLPGは、石油化学産業での産出として捉える。よって、LPG10単位は、石油化学産業における産出量を計算する式に計上する

LPG産業からの産出を考える（LPG産業を行方向でみた）場合、マイナス表記となっている石油化学産業、つまり、列が石油化学産業、行がLPG産業としてみた場合の交点である-10は、LPG産業へ10単位LPGが投入されたと考える。つまり、LPG10単位は、LPG産業における投入量を計算する式に計上する

というルールで、マイナス投入方式における投入と産出を扱うことについて言及しました。

マイナス投入方式の場合、重量単価が副産物が投入される産業のものになる

上記のルールに則って、単一産業での投入量、産出量、廃棄物発生量を推計するコードが、以下のようになります。

# x産業を0111（穀類）に固定
x = 0
# 投入量を計算
input = 0 # 投入分
fuel = 0 # 燃料使用分
output = 0 # 産出分
df_index = df_price_per_ton.index
for i in range(187):
   for k in range(len(df_price_per_ton.index)):
       Ui = df_price_per_ton.iat[k, 0]
       input_amount = df_iotable.iat[i, x] * 10**6
       if Ui == 0:
           continue
       if df_index[k] == df_iotable.index[i]:
           if input_amount >= 0:
               input += input_amount // Ui
               if df_index[k] == '2121': # 石炭製品の燃料使用分
                   fuel += input_amount // Ui
               # 石油化学系基礎製品への石油製品投入ではない場合
               if df_index[k] == '2111' and df_iotable.columns[x] != '2031':
                   fuel += input_amount // Ui # 石油製品の燃料使用分
           else:
               output += abs(input_amount) // df_price_per_ton.iat[x, 0]
           
# 産出量を計算
iyunyu = 0 # 移輸入
iyushutsu = 0 # 移輸出
consume = 0 # 消費
fixed_capital = 0 # 固定資本
stock = 0 # 在庫
Ux = df_price_per_ton.iat[x, 0]
if Ux == 0:
   output = 0
   consume = 0
   fixed_capital = 0
   stock = 0
   iyushutsu = 0
   iyunyu = 0
else:
   for i in range(187):
       if i == x:
           continue
       else:
           if df_iotable.iat[x, i] >= 0:
               output += df_iotable.iat[x, i] * 10**6 // Ux
           else:
               input += abs(df_iotable.iat[x, i]) * 10**6 // Ux
   

   ctuple = ('7111', '7211','7212', '7311', '7321')
   for c in ctuple:
       consume += df_iotable.loc['0111', c] * 10**6 // Ux
   
   ftuple = ('7411', '7511')
   for f in ftuple:
       fixed_capital += df_iotable.loc['0111', f] * 10**6 // Ux
   
   stock = df_iotable.loc['0111', '7611'] * 10**6 // Ux
   
   iyushutsu = df_iotable.loc['0111', '8100'] * 10**6 // Ux
   
   iyunyu = -(df_iotable.loc['0111', '8700']) * 10**6 // Ux

input = input + iyunyu
output = output + iyushutsu + consume + fixed_capital + stock
waste = input - output - fuel
print('投入分：' + str(int(input)) + '[t]') 
print('産出分：' + str(int(output)) + '[t]')
print('燃料使用分：' + str(int(fuel)) + '[t]')
print('廃棄物発生量：' + str(int(waste)) + '[t]')

ポイントは、マイナス投入方式の場合、重量単価が副産物が投入される産業のものになるというところでしょうか。

上記の例でいうと、LPG産業の重量単価が適用されるということですね。

重量単価初期値における推計値と統計値の比較・相関

重量単価初期値における廃棄物発生量の推計値と統計値の比較表は、以下のようになります。

製造業24業種のうち、10業種で推計値が負の値となり、飲料・飼料、はん用機器、木材、その他の製造業で大きくずれています。

また、値が0以下の業種を除いて散布図を記述すると、以下のようになります。

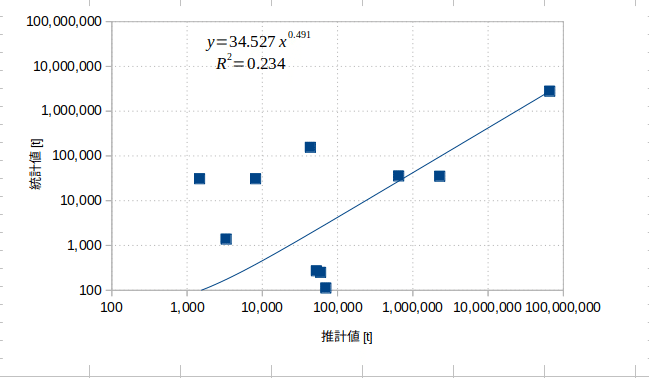
相関係数は0.234で、推計値と統計値の相関はあまりみられません。

最適化後の推計値と統計値の比較・相関

次に、最適化後の推計値と統計値の比較表が、以下のようになります。

また、推計値と統計値の比較を図で表すと、以下のようになります。

業務用機器、電子部品、情報通信機器、輸送用機器は推計値が負となるために、グラフから除きました。また、統計値が0である印刷、比較、非鉄金属もグラフから除きました。

先述の7つを除いたときの相関係数は、0.983となります。

相関の検定を再度行います。
有意水準は、1%とします。自由度が15なので、1%水準（両側検定）のt分布の値kは、2.9467。

検定統計量T = 0.983√(17-2)/√(1-0.983^2) = 20.8603

T＞kより、帰無仮説は棄却され、対立仮説を採用。つまり、有意水準1%で2変量（推計値と統計値）には相関関係があるといえます。