[Stataによるデータ分析]重力モデルの推定(3)
本コラムでは、重力モデルの推定(1)、(2)に続き、新貿易理論に基づく重力モデルを紹介します。なお、本コラムで使用するデータとプログラムは以下から利用可能です。
伝統的重力モデルのおさらい
重力モデルの推定(1)で紹介した推計式(1)式を再掲します。
$$
lnX_{ij}=\alpha+\beta_1lnDist_ij+\beta_2lnGDP_i+\beta_3lnGDP_j+\epsilon_{ij}
$$
この(1)式は伝統的重力モデルと呼ばれますが、かつては「理論的な裏付けがない」といった批判がありました。しかし、1980年代から90年にかけて登場した新貿易理論によって、理論的な裏付けが与えられるようになりました。これにより、従来の分析で使われてきた(1)式による重力モデルには深刻な欠陥があることが明らかとなり、理論的な革新が実証分析の方法の見直しを促すようになりました。
第三国効果
まず、新貿易理論が投げかけた伝統的重力モデルへの問題点について簡単に説明しましょう。伝統的重力モデルでは、基本的にA国B国間の貿易額はA国とB国の経済規模やA国とB国の二国関係を示す要因によって決まると考えます。しかし、実際の世界は複数の国によって構成されるので、A国とB国の貿易は他の国々の行動の影響も受ける。たとえば、今、A国、B国、C国の3カ国で構成されているとします。C国は資源も豊富で賃金も安いが政治的な事情で鎖国していたとします。このとき、A国とB国の貿易はA国、B国、およびA国とB国の間の輸送コストなどで決まります。しかし、ある日、C国は鎖国をやめA国やB国と貿易を始めたとしましょう。C国は資源が豊富で賃金が安いのでA国やB国に安い価格で商品を輸出したとします。A国は、B国から輸入する代わりにC国から輸入し、B国もA国の代わりにC国から商品を輸入するようになったとするとA国とB国の貿易は激減することになります。

現実の社会ではここまで極端な例はないかもしれないですが、この例から、A国B国の二国間の貿易は第三国であるC国の要因の影響も受けることがわかります。つまり、A国B国の二国間の貿易額を分析する際には、A国B国間の要因だけではなく、他の国々との関係も考慮しないと分析結果に歪が生じるということになります。この効果は第三国効果と呼ばれることもあります。
新貿易理論に基づく重力モデル
このコラムでは、詳細な理論的な背景については補論に譲り、直感的な説明を行います。新貿易理論では、輸入国の消費者の効用関数からスタートし、二国間貿易額を、輸入国(B国)における輸出国(A国)の商品の需要関数としてとらえます。そして、輸出国(A国)の商品の需要は、a) 輸出国(B国)の商品の価格$${p_AB}$$、b) 輸出国(B国)の商品の種類(品目数)$${N_A}$$、c) 輸入国(A国)の所得$${E_A}$$、d) 輸入国(A国)における第三国が提供する商品価格$${P_A}$$、の4つから構成されると考えます。ここでd) の価格指数$${P_A}$$は、第三国(上の図ではC国)が提供する商品価格が低下すれば、輸出国の商品の需要は低下すると考えます。
a) ~d) にはどんな変数をあてがえばいいでしょうか。a) は輸入国(A国)と輸入国(B国)の輸送費$${\tau_{AB}}$$(距離distance、FTAの有無に依存)と輸出国(B)国の価格$${p_B}$$、つまり$${p_AB=p_B*\tau_{AB}}$$b) と c) はそれぞれ輸出国のGDP($${N_B}$$)、輸入国のGDP($${E_A}$$)に比例すると考えます。d) は価格指数$${p_A}$$が入手できれば説明変数として加えることができます。これを式にすると以下のようになります。
$$
X_{AB}=f(lnGDP_A, lnGDP_B, Dist_{AB}, FTA_{AB}, p_B, N_B, E_A, P_A)
$$
この式を推定する際に問題となるのが価格指数$${P_A}$$をどのように用意するかです。これを用意するのはなかなか困難ですが、この式をよく見ると、輸出国が同じであれば輸出国のGDP($${N_B}$$)、輸出国の出荷価格$${p_B}$$は同じ値を、輸入国が同じであれば輸入国のGDP($${E_A}$$)と価格指数$${P_A}$$は同じ値をとります。
以下の表の上段は、A国(1)、B国(2)、C国(3)間の貿易額を分析する際の説明変数の組み合わせを示しています。
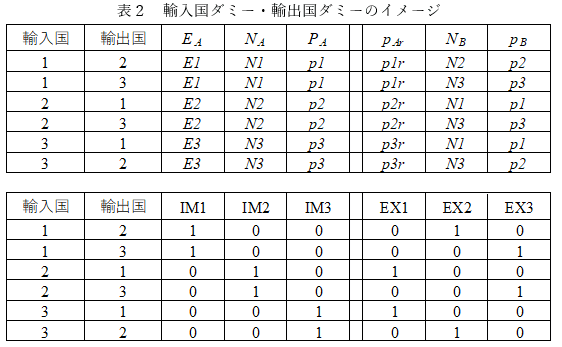
輸出国要因は、輸出国が同じであれば同じ値をとるので輸出国ダミーで、輸入国属性は輸入国が同じであれば同じ値をとるので、輸入国ダミーで置き換えてしまうというのが新貿易理論に基づく重力モデルです。上の表の下段のIM1, IM2, IM3は輸入国ダミー、EX1, EX2, EX3は輸出国ダミーを示します。結局、以下のように距離とFTAダミー、輸出国ダミー、輸入国ダミーを説明変数とする回帰式を推定することになります。
$$
lnX_{ij}=\alpha +\beta_1lnDist_{ij}+\beta_2lnFTA_{ij}+IM_i+EX_j+\epsilon_{ij}
$$
複数年のデータがある場合は、輸出国ダミー、輸入国ダミーを、輸出国-時点ダミー、輸入国-時点ダミーに置き換えます。
$$
lnX_{ijt}=\alpha +\beta_1lnDist_{ij}+\beta_2lnFTA_{ijt}+IM_{it}+EX_{jt}+\epsilon_{ijt}
$$
新貿易理論に基づく重力モデルは、需要構造を前提として重力モデルを定義することから構造重力モデル(Structural Gravity Model)と呼ばれます。
Stataによる新貿易理論に基づく構造重力モデルの推定
新貿易理論に基づく重力モデルを推定するには多数のダミー変数をいれることになります。こんなとき便利なのがreghdfeコマンドです。以下がプログラム例です。データはStataによるデータ分析第3版の3章で紹介したgravity-g20asean.dtaで、2015年におけるG20とASEAN加盟国の二国間貿易額です。reghdfeコマンドのabsorbオプションにはiso3_dとiso3_oが書き込まれていますが、それぞれ輸入国(destinationのd)と輸出国(originのo)の国番号(3桁)です。
use gravity-g20asean.dta,clear
gen lnTrade= log(Trade)
gen lndistance= log(distance)
gen lnGDPex=log(GDPex)
gen lnGDPim=log(GDPim)
gen lnPOPex=log(POPex)
gen lnPOPim=log(POPim)
reg lnTrade lnGDPex lnGDPim lndistance FTA
reghdfe lnTrade lnGDPex lnGDPim lndistance FTA,absorb(iso3_d iso3_o)推計結果は以下の通りです。まず、通常の最小二乗法(reg)による推定結果です。FTAの係数は0.512になりました。

次に、reghdfeコマンドによる構造重力モデルの推計結果です。この推計では、輸出国、輸入国のGDPは輸出国ダミー、輸入国ダミーと相関してしまうので、GDPの係数は計算されません。FTAの係数は0.356と少し小さな値になりました。

なお、このデータでは1時点のデータしか含まれていませんでしたが、複数時点のデータであれば、輸入国ー年ダミー、輸出国ー年ダミーが必要ですので、egen-groupコマンドで、輸入国ー年、輸出国ー年の番号を用意します。具体的には以下のように入力します。
egen iso3_d_year=group(iso3_d year)
egen iso3_o_year=group(iso3_o year)
reghdfe lnTrade lndistance FTA, abosrb(iso3_d_year iso3_o_year)本コラムはStataによるデータ分析入門第3版のWeb Appendixとして用意されました。
Stataによるデータ分析入門第3版のWEB補論の一覧はこちら。
より詳しく学びたい人にいくつか関連文献を紹介しておきます。
FTAや重力モデルなど基礎から学びたい人には京都大学の神事先生と慶応大学の清田先生による以下のテキストがおすすめです。
新貿易理論、そして最近は新々貿易理論が注目を集めていますが、一連の議論については、青山学院大学の田中先生のテキストを参照してみてください。
構造重力モデルの理論的背景など詳しく知りたい人には、ちょっと専門的ですが、以下の香川大学の山ノ内先生の本を薦めます。
2023年8月1日より、上記の山ノ内さんの「日本の自由貿易協定(FTA)の貿易総支出効果」のPDF版がJ-STAGEで無料公開されています。
