
[Rによるデータ分析入門]離散選択モデルの様々(4):カウント・データ
本コラムは「離散選択モデルの様々」では、
(1)多項ロジット・モデル
(2)順序ロジット・モデル(Ordered Logit Model)
(3)ヘックマンの二段階推定モデル
を紹介しましたが(4)ではカウント・データに用いるポワソン回帰モデル、負の二項分布モデルを紹介します。
カウントデータとは
カウントデータとは、営業マンの契約成約件数や、患者の通院回数
・連続変数だければどゼロまたは正の整数しかとならい
・ゼロが多い
といったデータを分析する際に使用します。
使用するデータ
ここではCameron and Trivedi (2009)で使用された、2002年のMedical Expenditure Panel Surveyに基づく、25歳から64歳の成人の診察回数のデータです。Sataのdta形式のものが多数出回っていますが、ここではCSVに変換したものを使います。
なお、Stataのdta形式のデータは以下から取得できます。
https://grodri.github.io/datasets/docvis.dta
Rのコードもおいておきます。このコードを動かすには、{tidyverse}{MASS}{pscl}{psych}{AER}のパッケージをインストールしておく必要があります。なお、MASSは負の二項分布モデルの推定、psclはゼロ過剰モデルの推定、AERはポアソン回帰モデルの妥当性チェックする検定に使います。
データの概観
#データ読み込み
dataf <-read_csv("docvis.csv")
psych::describe(dataf,skew=FALSE)
hist(dataf$docvis)
table(dataf$docvis)まず記述統計を見ておきましょう。describeでサンプル数(n)、平均値(mean)、標準偏差(sd)、最小値(min)・最大値(max)等を出力してみました。ここで被説明変数にするのはdocvis(医師の訪問回数=通院回数)です。通院回数は正の整数で最小値が0なのでゼロの値も含まれることがわかります。
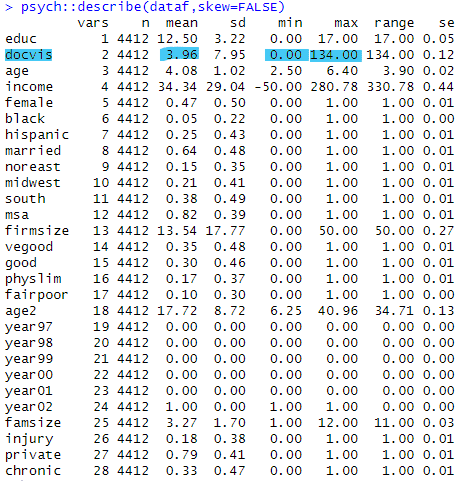
次にdocvisのヒストグラムを作成してみました。確かにデータの大半が0になっていることがわかります。

docvisは0-10件の値をとるサンプルが4000件ありますが、ごく一部ですが100を超えるようなサンプルもあるようです。さらにtable()関数で正確な件数をカウントしてみました。docvisが0のデータは1606あることがわかります。

ポアソン回帰モデル
このように、連続変数だければどゼロまたは正の整数しかとならい、ゼロが多いデータを扱う際に用いられるのがポアソン回帰モデルです。このモデルでは「滅多に発生しないことを分析する分布」であるポワソン分布を用います。事故や不良品の発生確率などがこの分布によく当たはまることから、品質管理の業界ではよく用いられるそうです。数学的な説明は各種テキストやWEBリソースに譲り、ここではRでどのように推計ができるかを消化します。
Rでの推定は、ロジット・プロビットと同様glm()関数を使い、family=probit、logiのところをpoisson(link="log")にします。具体的には以下のように記述します。
glm(y~x1+x2+x3+x4,data=データフレーム名,family = poisson(link = "log"))
では、普通の回帰分析の結果とポアソン回帰を比較してみましょう。被説明変数には医師訪問回数docvis、説明変数には民間保険加入状況(private)、健康状態(慢性, chronic)、女性ダミー(female)、所得(income)、民族(黒人, black、ヒスパニック, hispanic)を使います。ここでの問題意識は「民間保険に加入していると医師の受信回数が過剰になっているのではないか」というもので、privateの係数に注目します。
以下では最初にlm()関数による最小二乗法、次にglm()によるポアソン回帰モデルを推定します。
result1 <- lm(docvis~private+chronic+female+income+black+hispanic,data=dataf)
summary(result1)
result2 <- glm(docvis~private+chronic+female+income+black+hispanic,data=dataf,family = poisson(link = "log"))
summary(result2)最初は最小二乗法の結果です。ほとんどの説明変数が統計的に有意になりましたが、blackだけ非有意となりました。

次にポアソン回帰の結果です。係数の符号は最小二乗法のときと同じですが、今度はblackも含めすべての変数が統計的に有意になりました。

係数の符号についても見ておきましょう。privateの係数がプラスなのでやはり民間医療保険に入っていると医師の受診回数が増えることがわかります。chronic慢性疾患が多い人も受診回数が多い、女性や所得の高い人も受診回数が多いという結果を得ました。一方、黒人やヒスパニックは係数がマイナスなので受診回数がすくないと読めます。
ポアソン回帰の係数の意味
ポアソン回帰の係数の意味ですが、xが1増えるとyは$${ \beta*100}$$%増えると解釈できます。これはポアソン回帰の限界効果が
$$
\frac{\partial E[y|x]}{\partial x}=\beta E[y|x]
$$
で、これを変形すると、
$$
\frac{\partial E[y|x]}{E[y|x]}=\frac{\Delta y}{y}=\beta \Delta x
$$
と表せるからです。
ポアソン回帰と線形回帰の係数の比較
線形回帰(最小二乗法)とポアソン回帰の係数の比較する際には注意が必要です。まず、最小二乗法の場合、xの限界効果は、
$$
\frac{\partial E[y|x]}{\partial x}=\beta
$$
です。ポアソン回帰の限界効果は、xが連続変数の場合、
$$
\frac{\partial E[y|x]}{\partial x}=\beta E[y|x]=\beta \bar{y_i }
$$
となります。ここでβは係数、$${ \bar{y_i }}$$は被説明変数のyの平均値です。たとあえばincomeの場合、ポアソン回帰の係数は
0.003、被説明変数のyの平均値はおよそ4なので、0.012になります。最小二乗法のincomeの係数は0.014ですから、ポアソン回帰のほうが、ごくわずかですが小さいことが分かります。
ポアソン回帰モデルの仮定の妥当性の検定
ポアソン回帰モデルは、ポアソン分布を前提としていますがこの分布には「平均($${\mu=E[y|x]}$$)と分散($${Var[y|x]}$$)が等しい」という強い仮定が課されています。この仮定がみたされているかどうかの検定がいくつか提案されています(詳しくはKleiber and Zeileis, 2008のP.133-135、Greene (2017)のP.888-889を参照のこと)。
ここでは2つの検証方法を紹介します。一つは、
$$
検定1 Var(y|x)=(1+\alpha ) \mu
$$
で1+αが1より大きいかを検定する方法、もう一つは、
$$
検定2 Var(y|x)=\mu + \alpha \mu^2
$$
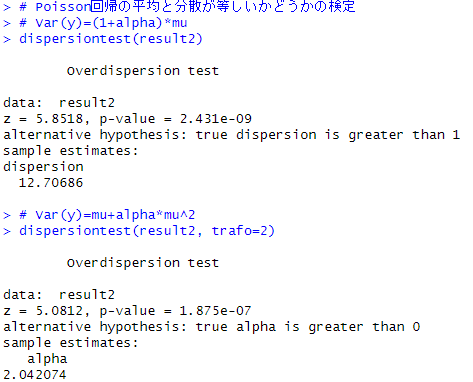
でαが0より大きいかを検定する方法です。この検定には{AER}パッケージに含まれるdispersiontestという関数を使います。
検定1は、dispersiontest(ポアソン回帰の結果オブジェクト)
検定2は、dispersiontest(ポアソン回帰の結果オブジェクト, trafo=2)
で検定ができます。以下は検定の結果で、検定1も検定2もp-valueが小さいので帰無仮説が棄却され、対立仮設(Alternative hypothesis)が支持されます。
負の二項分布モデル
そこで、この仮定を緩めて推定する方法として提案されている方法が負の二項分布モデルです。負の二項分布モデルについても詳細は省略しますが、ポアソン回帰モデルの一般形で、θという追加的な説明変数が加わるのですが、このθが∞のとき負の二項分布モデルとポアソン回帰モデルは等しくなることが知られています。負の二項分布モデルを推定するには、MASSパッケージに含まれるglm.nb()関数を用います。
glm.nb(y~x1+x2+x3+x4,data=dataf,link = "log")
さっそくコードと結果を見てみましょう。
result3 <- glm.nb(docvis~private+chronic+female+income+black+hispanic,data=dataf,link = "log")
summary(result3)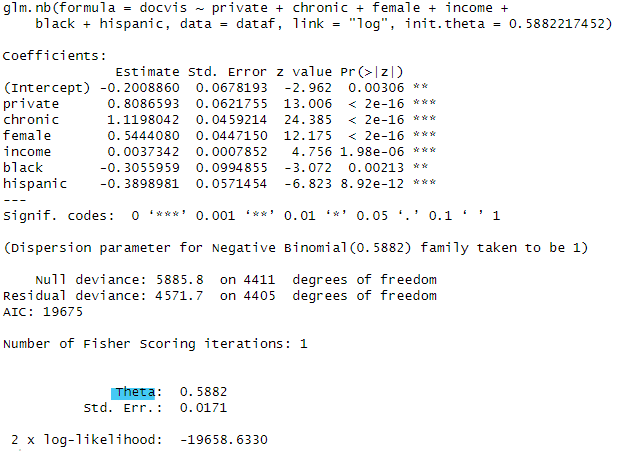
ゼロ過剰モデル
ここまで紹介したポアソン回帰、負の二項分布モデルはいずれもゼロが多い時には適切ではないことが知られています。前述の通り今回の事例で使用しているデータでも、yである医師訪問回数docvisで約4000件のうちゼロ値は1606件ありました。さらに、上記のポワソン回帰の推計式からdocvisの0-9までの実績値と予測値を比較すると、

0のところで実績値(actual)と予測値(pred)の乖離が大きくなっていることがわかります。
このように被説明変数にゼロが多い場合には、被説明変数がゼロかどうかの決定要因、被説明変数がゼロ以上のとき決定要因をそれぞれ別の係数で推計するゼロ過剰ポアソン回帰モデル(Zero-inflated Poisson Regression Model)あるいはゼロ過剰負の二項分布モデル(Zero inflated Negative Binomial Model)の利用が推奨されています。詳細は参考文献に譲りますが、ここではRによる推定方法と結果の解釈方法について説明します。
zeroinflによる推定
ゼロ過剰モデルはpsclライブラリーに含まれるzeroinfl()関数を使います。予めpsclをインストールしておいてください。zeroinfl()の使い方は以下の通りで、|の前に被説明変数がゼロ以上のときの決定要因を、|の後ろに被説明変数かゼロかどうかの決定要因を並べます。また、distオプションでポワソン回帰か負の二項分布モデルかを選ぶことができます。
zeroinfl(y~x1+x2+x3|x2+x3,data=データフレーム名, dist="poisson")
zeroinfl(y~x1+x2+x3|x2+x3,data=データフレーム名, dist="negbin")
注意が必要なのが、|よりも後ろの「被説明変数かゼロかどうかの決定要因」の結果の見方です。たとえばx2が大きくなれば、被説明変数が非ゼロの大きな値になるといった傾向にある場合、|の前のx2の係数はプラスなりますが、|の後ろのx2の係数はマイナスになります。というのは、|の後ろは被説明変数は0になる確率への影響を示すからです。
以下の結果はゼロ過剰ポアソン回帰モデルの推計結果です。上段のCount model coefficientsのところが被説明変数がゼロ以上のときの係数です。下段のzero-inflation model coefficientsのところは被説明変数がゼロになる確率の決定要因になります。上段と下段で係数がすべて逆になっていることに注意してください。

次にゼロ過剰負の二項分布モデルです。
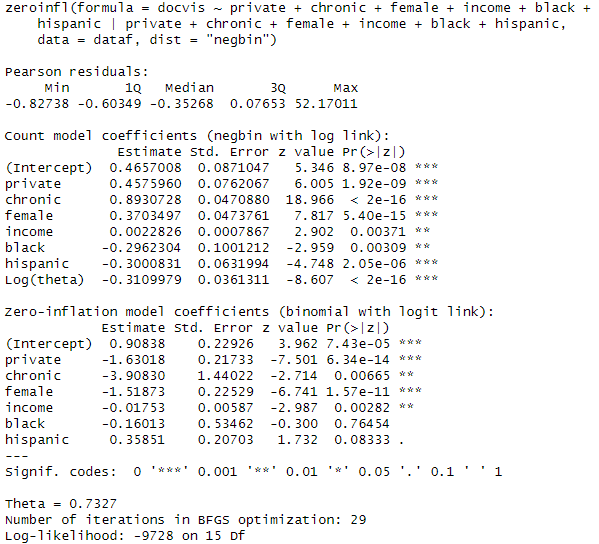
ゼロ過剰ポアソン回帰モデルと同様に上段と下段で係数がすべて逆になっているいます。ここでも実績値と予測値を比較しておきましょう。pred_poisはゼロ過剰ポアソン回帰モデルからの予測値、pred_nbはゼロ過剰二項分布モデルからの予測値です。ゼロ過剰モデルを用いたほうが0の値の予測精度が上がっていることが分かります。また、全体的にpred_nbのほうがフィットがよさそうだと判断できます。

モデル間の比較
最後にポアソン回帰モデル、負の二項分布モデル、ゼロ過剰ポアソン回帰モデル、ゼロ過剰負の二項分布モデルの4つの推計結果のどれが最も説明力が高いかを比較する方法についてふれておきます。これらのモデルは非線形モデルなので決定係数が使えません。こんなときに使われるのがAkaike’s Information Criteria、略してAICです。このAkaikeですが、これは日本人研究者の赤池弘次氏が開発したことにちなんで名づけられています。
細かい説明は省きますが、この指標が小さいほうが説明力が高いと解釈できます。Rでは、AIC(結果オブジェクト1, 結果オブジェクト2)のように記述すると結果1と結果2のAICを計算してくれます。ここではresult2からreulst5までのAICを比較してみましょう。

AICが小さくなるモデルが最良なのでここではresult5がAICが最小になっており、説明力が高いと判断できます。ポアソン回帰モデルは軒並みAICが大きいので、ポアソン回帰モデルで平均=分散という強い仮定がおかれていることにより説明力が悪くなっているのかもしれません。
参考文献
詳しくは以下の参考文献を参照してください。
ウィラワンードニ-ダハナ・勝又壮太朗「Rによるマーケティング・データ分析」新世社 第8章 カウントデータの分析
Kleiber and Zeileis, Applied Econometircs with R
5.3 Regression Model for Count Dataに説明があります。
Heiss, Using R for Introductory Econometrics
17.2 Count Dataに説明があります。
Green, W., 2017, Econometric Analysis, 8th Edition, 第8章4節(P.884-)に説明があります。
本コラムは「Rによるデータ分析入門」のWEBサポートページとして作成されました。WEBサポートの一覧は以下を参照してください。
WEBサポートの一覧は以下を参照してください。
