[Rによるデータ分析入門]対数による回帰分析でエラーが出るときの対処法

Rで変数に対数をとって回帰分析する際にエラーが出る場合があるのですが、本コラムではその対処方法について説明します。

そもそも回帰分析でなぜYとXに対数をとるの？という疑問については、様々なWEB記事で紹介されていますが、特に以下のコラムを一読することをおすすめします。

回帰分析で変数の対数を取る理由はなんでだっけ？ - データ分析メモと北欧生活

はじめに

Rで変数に対数をとって回帰分析する、今、データフレーム名がdataf, 被説明変数がY、説明変数がXのときにlm(log(Y)~log(X),data=dataf)を実行した際にエラーが出て進めなくなることがあります。たとえば、以下のようなエラーメッセージが出てきます。

これはYやXにゼロ、あるいはマイナスの値が含まれると対数が取れないのでエラーがでます。Yがどのような変数化に応じて次の3つ対処方法があります。

対処法１ ゼロやマイナスになることが不自然な変数の場合

そもそもYにゼロやマイナスが入っていること自体が不自然（たとえば身長とか体重、ゼロは異常値）
→yがプラスの値をとるデータに限定する
dataf <- dataf &>&dplyr::filter(Y>0)

対処法２　被説明変数に１を足してから対数をとる

被説明変数がゼロ値をとるサンプルも分析に加えたい場合、被説明変数に１を足してしまえば対数をとることができます。具体的には、lm(log(Y+1)~log(X),data=…)のようにlm()関数の中に計算式を入れて計算することができます。

対処法３ マイナスの値をとる変数の場合

Yが「経常利益」のようにマイナスにもプラスにもなりうる変数の場合
→対数ではなく何らかの変数に対する比率にする、経常利益であれば売上利益率や総資産利益率(ROA)にする

対処法４（特殊ケース）ポアソン疑似最尤法の利用

国際貿易の実証分析では、被説明変数に二国間貿易額の対数値、説明変数に輸出国と輸入国のGDP対数値、二国間距離の対数値を用いた重力モデルがよく使われます。被説明変数にゼロの値が入ってくると対数が取れない、という問題に対処するために開発されたポアソン疑似最尤法(Poisson Pseudo Maximum Likelihood, PPML)という手法よく使われます。具体的には

$$
Trade_{ij}=exp(\beta_1 log(GDP_i)+\beta_2 log(GDP_j)+\beta_3 log(Distance_{ij})+\beta_4 RTA+\epsilon_{ij})
$$

という非線形モデルを推定します。ここで$${exp(X)}$$は指数関数で、$${Y=exp(X), X=log(Y)}$$という関係にあります。つまり、$${Y=exp(log(X))}$$の両辺を対数化すると、$${logY=log(X)}$$となるので、上記の式は、$${log(Trade)=\beta_1 log(X)…}$$という推定式と同じであることがわかります。上記の式では被説明変数は対数を取っていませんので０の値が含まれて問題なく推定できます。
この式は一見複雑そうですが、Rではgravityというパッケージ含まれるppml()という関数で推定が可能です。

具体例：重力モデル

ここでは二国間貿易額のデータを使った重力モデルの推定を例に、対数がとれない場合の対処方法について説明します。重力モデルについては以下に解説があります。

使用するデータはフランスのシンクタンク、CEPIIが収集・加工・提供する重力モデル・データです。

CEPII - Data

今回使用するデータとスクリプトは以下からダウンロードできます。

WS-log-w-missing.R

1.95 KB

ファイルダウンロードについて

ダウンロード

gravity-data1985.csv

1.35 MB

ファイルダウンロードについて

ダウンロード

このデータには様々な変数が含まれますが、flow: 二国間貿易額、gdp_o: origin country（輸出国）のGDP、gdp_d: destination country（輸入国）のGDP、distw: 二国間の距離、rta: 地域貿易協定ダミーの５つの変数に注目します。
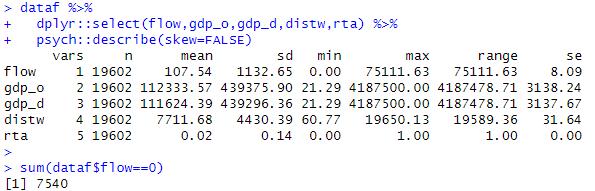
readr_csv()でデータを読み込んで、基本統計量を見てみましょう。psych:: describeでサンプル数(n)をみてみると、gdp_o, gdp_dで数が少なくなっています。これは欠損値だと考えられます。
　また、sum(dataf$flow==0)ですが「"data$flow==0"の条件を満たすサンプルを足し合わせろ」の意味になり、flowがゼロになっているサンプル数をカウントしてくれるのですが、7540ということで19602のうちflowがゼロなのが8000弱あることがわかります。

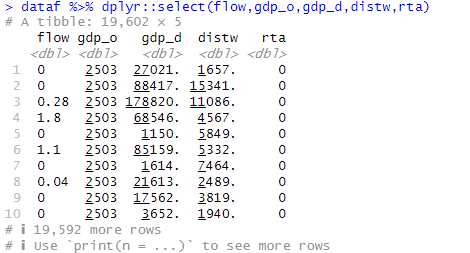
念のためデータを確認してみましょう。dplyr::select()で変数を限定して画面に表示させていますが、たしかにflowがゼロのサンプルが多数あります。

lm()の中でlog()を使って対数化して回帰分析を実施すると、以下のようなエラーが出ます。

重力モデルによる実例：対処法１

そこで、対処法１をやってみましょう。dplry::filter(flow>0)でflowが0以上のサンプルだけで構成されるデータフレームdataf_nzeroを作成し、このデータで回帰分析を実施すると結果が出てきました！

下から3行目に、Residual sandard error: 2.235 on 12057 degrees of freedomという表記がありますが、degrees of freedom（自由度）はサンプル数―説明変数の数ー１なので今説明変数が4つあるので、サンプル数は12057+5=12062になります。また、距離の係数は、二国間距離が１％増えるとどの程度貿易量が変化するかを示しますが、今、-1.12になっています。またrta(二国間の地域貿易協定の有無)ダミーの係数は1.08でｔ値も高いの統計的に有意であることから、二国間地域貿易協定があると貿易額が大きいことが示唆されます。

重力モデルによる実例：対処法２

次に、被説明変数に１を足してから対数をとってみましょう。lm(log(Y+1)~log(X),data=…)のようにlm()関数の中に計算式を入れています。

下から4行目に、Residual sandard error: 1.318 on 19597 degrees of freedomという表記がありますが、今度は自由度は19597となりました。サンプル数は19597+5=19602と対処法１のときよりも7500ほどサンプル数が増えました！被説明変数がゼロになっているサンプルも推計に追加されたからです。そして、係数も変わっていることに注目してください。距離は係数は-0.6と対処法１のときよりも小さな数値になりました。一方、rtaの係数は1.47と対処法１のときよりも大きくなりました。

重力モデルによる実例：対処法４

今回のデータではflowにマイナス値は含まれないので対処法３の実例は割愛します。対処法２で被説明変数にゼロが含まれるデータも分析に含めることができたので、これで問題がないように思えますが、これまでの国際貿易の実証分析では、log(Y+1)による推計は偏りをもたらすことがSantos and Tenreyro (2006)によって示されています。

J. M. C. Santos Silva, Silvana Tenreyro; The Log of Gravity. The Review of Economics and Statistics 2006; 88 (4): 641–658. doi: https://doi.org/10.1162/rest.88.4.641

The Log of Gravity

詳細な議論は割愛しますが、Santos and Tenreyro (2006)はPPMLという推計方法（ppml()関数）を利用することを推奨しています。これはポアソン回帰という呼ばれる被説明変数にゼロの値が多数含まれるデータを用いる際に使われる推計方法を応用したものです。ポアソン回帰について以下も参照してみてください。

ppml()関数gravityパッケージに含まれるので、事前にgravityパッケージのインストールし、library(gravity)で呼び出しておくことが必要です。このppml()関数は重力モデルを推計するために用意されたものなので変数の入れ方がやや独特です。今、二国間貿易額をY, 距離をX1、輸出国と輸入国のGDPの対数値をlogX2, logX3とすると、
ppml(dependent_variable="Y", distance="X1", additional_regressors=c(logX2, logX3), data=….)
と書きます。ppml()関数は距離以外の変数で対数をとるべきものがあれば事前に対数化しておく必要があります。結果をみてみましょう。

事前準備として輸出国と輸入国のGDPを対数化します。

dataf <-dataf %>% mutate(lgdp_o=log(gdp_o), lgdp_d=log(gdp_d),)

距離はppml()が対数化してくれるので対数化する必要はありません。
今回のデータでPPMLを推定するには、以下のように書きます。

model_linear <-ppml(
dependent_variable = "flow",
distance = "distw",
additional_regressors = c("rta", "lgdp_o", "lgdp_d"),
data = dataf
)
summary(model_linear)

以下が推計結果です。距離の係数はrta係数は0.44と小さくなりました。

本コラムは「Rによるデータ分析入門」のWEBサポートページとして作成されました。WEBサポートの一覧は以下を参照してください。

Ｒによるデータ分析入門―経済分析の基礎から因果推論まで― | 松浦 寿幸 |本 | 通販 | Amazon

WEBサポートの一覧は以下を参照してください。

R-text-web-support