[Stataによるデータ分析入門]差の差の分析の数式表現

本コラムは、Stataによるデータ分析入門第3版の第5章差の差の分析、5.2.1節都市開発の効果測定の補論です。

Stataによるデータ分析入門 第3版 ~経済分析の基礎から因果推論まで

本文の事例では、鉄道延伸によって1999年に乗換駅となった神奈川県藤沢市の湘南台駅最寄りの賃貸物件を処置群（Treatment）、その近隣駅を最寄りとする物件を比較群（Control）として、差の差の分析（1999年と2004年の変化を処置群と比較群で比較）により鉄道延伸の影響を評価する方法について紹介しました。
本コラムでは、差の差分析を以下の回帰式で表し、そして処置効果が以下の式の$${ \gamma }$$で表されることを示します。

$$
Y_{it}=\alpha +\beta X{it} +\eta Treat +\gamma Treat_{04} +\delta Year_{04} +u_{it}
$$

ここで、処置群（T）、比較群（C）を年毎に平均したものを、$${ \bar{X_{T99} }, \bar{X_{T04} }, \bar{X_{C99} }, \bar{X_{C04} }, \bar{Y_{T99} }, \bar{Y_{T04} }, \bar{Y_{C99} }, \bar{Y_{C04} } }$$で表します。また、単純化のため誤差項($${u_{it} }$$)は省略します。

まず、処置群の2時点の変化について考えてみましょう。処置群では、$${Treat, Treat_{04}}$$は１になります。2004年のデータでは、$${Year_{04}}$$も1になります。

ここで、２から１を引くと、$${\eta Treat}$$は打ち消されますので、以下を得ます。

次に、比較群の2時点の変化についてみましょう。$${Treat, Treat_{04}}$$はともに０になることに注意してください。

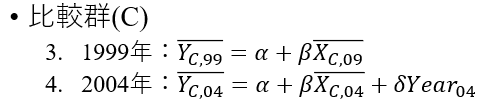
４から３を引くと、以下を得ます

ここで「処置群の二時点の差（2-1）」と「比較群の二時点の差（4-3）」の差をとると以下のようになります。

右辺の第１項、青字の部分は、観察される物件属性Xの変化がYの差の差の及ぼす影響を表します。

一方、赤字の$${ \gamma Treat_{04} }$$は、物件属性以外の要因でYの差の差の変化させる効果を示します。この事例では、処置群では鉄道路線の新設されたのに対して、比較群では変化がありませんので、$${ \gamma Treat_{04} }$$が鉄道延伸の効果を示すと解釈できます。
よって、最初の式に戻ると、以下の式を推定して、$${ \gamma }$$の係数に注目することで差の差分析の処置効果をみることができます。

$$
Y_{it}=\alpha +\beta X{it} +\eta Treat +\gamma Treat_{04} +\delta Year_{04} +u_{it}
$$

「Stataによるデータ分析入門第3版」のWEB補論の一覧はこちら。

stata-text-web-support