
[Rによるデータ分析入門]変量効果モデルと相関変量効果モデル(3)
本コラムでは、変量効果モデルがなぜ使われなくなったかについて説明した(1)と、変量効果モデルの問題点を克服する相関変量効果モデルについて紹介した(2)の内容を受けてRで変量効果モデルと相関変量効果モデルを推計する方法について説明します。(1)と(2)の内容を確認したい人は以下を参照してください。
下準備
今回使用するパッケージは、{tidyverse}, {plm}, {modelsummary}, {wooldridge}、比較のため{fixest}も使用します。予めインストールしておいてください。 データは{wooldridge}パッケージに含まれる米国の若年男性労働者の賃金データであるwagepanを使用します。サンプルのRスクリプト(WS-CRE.R)は以下からダウンロードできます。
データの読み込み
データの読みこみはdata()で行います。wooldridgeパッケージをインストールしていれば、以下でwagepanのデータを読み込むことができます。
data(wagepan,package='wooldridge')このデータはnrが個人番号、yearが調査時点、賃金の対数値lwageなどが含ま
れています。その他、教育年数educ、結婚ダミーmarried、労働組合への参加状況unionなどが含まれています。selectでいくつかの変数に絞って、データを画面表示させて見てみましょう。
wagepan %>% select(nr, year, lwage, married, union, educ)
nrが個人番号、yearが調査年です。たとえばnr=13の人1980年にはunion労働組合に入っていなかったのですが、1981年には加入、1982年には離脱しています。このようにunionは時間を通じて変化する変数になっています。ここに表示されている13番、17番、18番、45番の人たちはmarriedが常に0か常に1になっていますが、中にはサンプル期間中に結婚したり離婚したりする人もいるのでmarriedも時間を通じて変化する変数です。educは教育年数で、働きながら夜間学校に通う人もいてもおかしくなさそうですが、今回のデータでは期間中に教育年数が変化する人はいません。よって教育年数educは時間を通じて変化しない変数になっています。
feols()による固定効果モデルの推定
まず固定効果モデルで、賃金(対数値)を被説明変数、結婚ダミー、労働組合参加ダミー、教育年数を説明変数とする回帰式を推定してみましょう。
res_feols1 <- fixest::feols(lwage~married+union+educ,data=wagepan)
res_feols2 <- fixest::feols(lwage~married+union+educ|nr,data=wagepan)
res_feols3 <- fixest::feols(lwage~married+union+educ|nr+year,data=wagepan)
fixest::etable(res_feols1,res_feols2,res_feols3)feolsでは被説明変数~説明変数の後ろに|個体固定効果+時間固定効果と書くことで固定効果を入れることができます。最初の推定式は固定効果なし、次の推計式は個体固定効果のみ、3つ目は個体固定効果+時間固定効果の推計式です。推定結果は以下の通りです。

res_fols2とres_fols3は個体固定効果が入っていますが、これを加えると時間を通じて変化する説明変数は除外されます。今回の場合、教育年数educがこれに該当とするのでeducの係数が消えていることがわかります(今回のデータでは期間中に働きながら学校に通っていて教育年数が変化する人がいない)。また、固定効果をいれるとmarriedとunionの係数が小さくなっていることがわかります。なお、固定効果モデルでは個体固定効果と時間固定効果の両方を入れるのが基本となっています。
変量効果モデルの推定
次に変量効果モデルと固定効果モデルの結果を比較してみましょう。変量効果モデルを推定するには{plm}パッケージを使用します。最初にplm::pdata.fram()関数でデータがパネルデータであることをRに認識させます。書き方は以下の通りです。
plm::pdata.fram(データフレーム名, index=c("個体番号", "時間変数"))
今回場合データフレーム名はwagepan, 個体番号はnr、時間変数はyearです。
pdataf <- plm::pdata.frame(wagepan,index=c("nr","year"))モデルの推定はplm関数を使います。
plm(y~x1+x2,model=“モデルのタイプ”, effects=“固定効果の形式”, data=データフレーム)
ここで“モデルのタイプ”は、”pooling”, “within”(固定効果), “random”(変量効果)となります。
effectsは、個体効果と時間効果を入れる場合は”twoways”を指定します。effectsを省略すると個体固定効果のみの推計になります。
regs <- list(
"Pooling" =plm::plm(lwage~married+union+educ,data=pdataf,model="pooling"),
"Fixed-effect" =plm::plm(lwage~married+union+educ,data=pdataf,model="within"),
"TW-Fixed-effect" =plm::plm(lwage~married+union+educ,data=pdataf,model="within",effect="twoways"),
"Random-effect" =plm::plm(lwage~married+union+educ,data=pdataf,model="random"),
"TW-Random-effect" =plm::plm(lwage~married+union+educ,data=pdataf,model="random",effect="twoways")
)
msummary(regs,stars=TRUE, gof_omit='RMSE|AIC|BIC|Log.Lik.')これを実行するとmsummaryで結果表がViewerに出力されます。
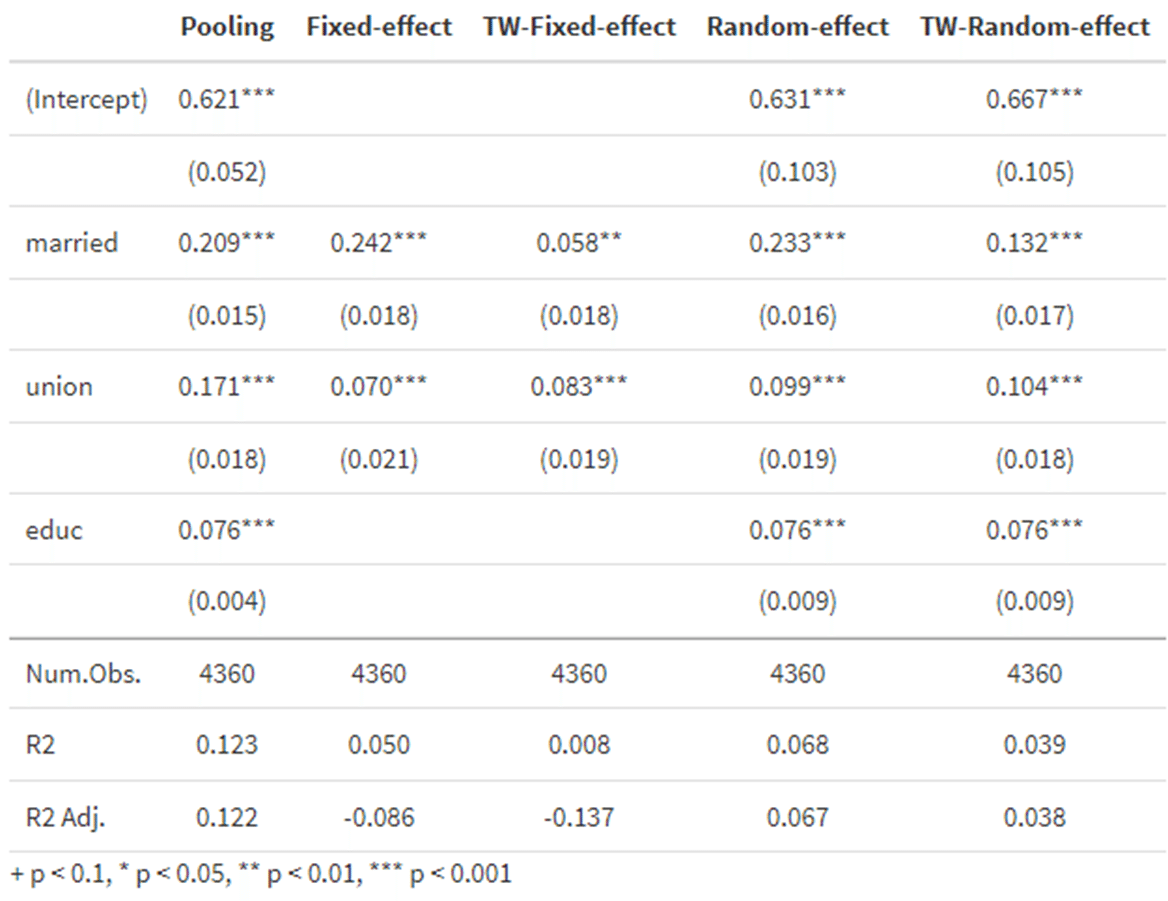
最初の3列は固定効果なし、個体固定効果のみの固定効果モデル、個体・時間固定効果を含む固定効果モデルで、feolsの結果と全く同じ結果が得られています。
4列目と5列目が変量効果モデルで、4列目が個体固定効果のみ、5列目が個体固定効果と時間固定効果の両方を考慮したモデルです。変量効果モデルでは時間を通じて変化しない変数、educの係数も得られていることがわかります。一方、unionやmarriedの係数に注目すると、3列目の固定効果モデルの推計値よりも大きくなっていることがわかります。
ハウスマン検定
「変量効果モデルと相関変量効果モデル(1)」で紹介した通り変量効果モデルはいろいろと問題のある推定方法で最近はあまり利用されなくなっています。また、それに伴い、変量効果モデルと固定効果モデルを選択するハウスマン検定も使用されることが少なくなっているのですが、一応、Rではphtestという関数で利用できますので一応紹介しておきます。
ハウスマン検定:plm::phtest
res1 <-plm(lwage~married+union+educ,data=pdataf,model="random")
summary(res1)
res2 <-plm(lwage~married+union+educ,data=pdataf,model="within")
phtest(res1,res2)まず、plmで変量効果モデルと固定効果モデルを推定します。上記の例では、それぞれの結果をres1、res2に格納し、これらをphtest()関数に導入します。結果は以下の通りです。帰無仮説は「変量効果モデルが正しい」ですが、これが正しい確率は0.001199と著しく小さいので、変量効果モデルは正しくない→固定効果モデルが妥当、と解釈します。

相関変量効果モデルの推定
相関変量効果モデルは「変量効果モデルと相関変量効果モデル(1)」で紹介した通り、説明変数に時間を通じて変化する変数の平均値$${\bar{X_i}}$$を導入します。ここで、
$$
\bar{X_i}=\frac{1}{T} ( X_{it=1} + X_{it=2} +…+ X_{it=3} )
$$
です。もう一度、相関変量効果モデルについて確認したい方はこちら。
まず、個体ごとの平均値を計算します。
pdataf <- pdataf %>%
group_by(nr) %>%
mutate(
m_married=mean(married),
m_union=mean(union),
)上記ではgroup_by()で個体ごとのグループを作成し、グループごとにmarriedやunionの平均値を計算し、これをm_married, m_unionと名付けています。これを説明変数に追加して変量効果モデルで推定することで相関変量効果モデルの推定が可能です。
以下のスクリプトでは、プーリング回帰(Pooling, 固定効果なし)、固定効果モデル(Fixed-Effect)、変量効果モデル(Random Effect)の3つに続いて、CRE1、CRE2の2つを推定します。この2つには、model="random"のオプションがついているので変量効果モデルで推定がお粉れていますが、時間を通じて変化する変数の平均値が説明変数に追加されているので相関変量効果モデル(Correlated Random Effect model)になります。CRE1では、上記で作成したm_marridとm_unionが追加されていますが、CRE2ではBetween(married)とBetwee(union)という変数が入っています。このBetween()関数はplmパッケージに含まれる関数で、個体ごとに平均値を計算する関数なので、それぞれm_marriedとm_unionと同じ変数が説明変数に追加されます。
regs <- list(
"Pooling" =plm::plm(lwage~married+union+educ,data=pdataf,model="pooling",effect="twoways"),
"Fixed-effect" =plm::plm(lwage~married+union+educ,data=pdataf,model="within",effect="twoways"),
"Random-effect" =plm::plm(lwage~married+union+educ,data=pdataf,model="random",effect="twoways"),
"CRE1" =plm::plm(lwage~married+union+educ+m_married+m_union,data=pdataf,model="random",effect="twoways"),
"CRE2" =plm::plm(lwage~married+union+educ+Between(married)+Between(union),data=pdataf,model="random",effect="twoways")
)
msummary(regs,stars=TRUE, gof_omit='RMSE|AIC|BIC|Log.Lik.')以下が推計結果です。CRE1とFixed-Effect、Random-Effectを比較してみましょう。CRE1は変量効果モデルがベースなので時間を通じて変化しないeducの係数が得られていることがわかります。一方、時間を通じて変化する変数の平均値m_marriedとm_unionを説明変数に入れている点が変量効果モデルと異なる点ですが、これらの変数を考慮することでCRE1のmarriedやunionの係数は、変量効果(Random-Effect)モデルのそれよりも小さく、固定効果(Fixed Effect)モデルの係数に近づいていることがわかります。このように、CRE1は時間を通じて変化しない変数を追加できるという変量効果モデルの特質と、説明変数と相関する個体属性を個体属性の平均値で考慮することで固定効果モデルのと特質を兼ね備えていることが伺えます。
CRE2は、m_married、m_unionの代わりにBetween(married)、Between(union)を追加した推計結果です。CRE1とCRE2は全く同じ結果になっていることから分るように、時間を通じて変化する変数の平均値をわざわざ計算しなくても、Between()関数を使えば、簡単に時間を通じて変化する変数の平均値を説明変数に導入できることがわかります。

変量効果モデルが正しいかどうかの検定
最後に、「m_marreidやm_union(あるいはBetween(married), Between(union))の係数がともに0である」かどうか調べる方法について考えましょう。もし、これらの係数が0であれば、変量効果モデルが正しいことになります。
複数の変数が同時にゼロかどうかを検定するには{car}パッケージのlinearHypothesis()関数を使います。使い方は、
linearHypothesis(結果オブジェクト名, matchcoefs(結果オブジェクト,"変数の名前の一部")
で、結果オブジェクトには参照する回帰分析の結果オブジェクト名、matchcoefsで、どの結果オブジェクトのどの係数に着目するかを指定します。ここでは、"Between"で始まる変数の係数が同時にゼロかを検定します。以下がスクリプト例です。
library(car)
res3 <- plm::plm(lwage~married+union+educ+Between(married)+Between(union),data=pdataf,model="random",effect="twoways")
linearHypothesis(res3,matchCoefs(res3,"Between"))今、相関変量効果モデルの結果をres3に格納しており、res3のうち"Betwee"で始まる変数の係数がともにゼロであるかどうかを検定してます。検定結果は以下の通りです。

赤で下線を引いたところが、「Betweeで始まる係数の係数がともにゼロである」確率です。今、0.1562%ですので確率が非常に小さく、この仮説は棄却れる、つまり正しくないと判断されます。Betweeで始まる係数の係数がゼロでないとすると変量効果モデルは正しくない、と結論付けることができます。
なお、一連のコラムの(3)の内容はFlorian Hessによる"Using R for Introductory Econometrics”を参考にしています。
Amazonは紙の本しか扱っていませんが、電子版は以下の際から購入できます。https://www.urfie.net/
本コラムは「Rによるデータ分析入門」のWEBサポートページとして作成されました。WEBサポートの一覧は以下を参照してください。
WEBサポートの一覧は以下を参照してください。
