ニューラルネットワークの予測の不確実性(Stochastic gradient Langevin dynamics・実装編)
はじめに
ニューラルネットワークの予測の不確実性を算出する手法を検証します。
jupyter notebookは下記にあります。
https://github.com/toshi-4886/neural_network/blob/main/uncertainty/4_SGLD.ipynb
概要
連続値を予測する回帰のためのニューラルネットワークを構築
Stochastic gradient Langevin dynamics (SGLD) で予測の不確実性を算出
Stochastic gradient Langevin dynamics
確率的勾配降下法とランジュバン動力学によるを組み合わせて、パラメータの事後分布をサンプリングする手法です。
SGLDの更新式に従ってパラメータを更新し、その過程のパラメータを事後分布からのサンプリングとして近似的に使用します。
SGLDの更新式は、差分プライバシーを保証した確率的勾配法(DP-SGD)と等価であることが知られています。
DP-SGDの更新式は下記で定義されます。
$$
\Delta \theta = \eta \biggl( \frac{1}{b} \sum_{i} {\rm clip}C (\nabla \log p(y_i|x_i, \theta)) + \frac{1}{n}\nabla{\theta} \log p(\theta) + \mathcal{N}(0,\sigma^2c^2\rm{I}) \biggr)
$$
ここで、$${{\rm clip}_C}$$はベクトルのL2ノルムを最大$${C}$$に制限する関数、$${\eta}$$は学習率、$${c}$$と$${\sigma}$$はDP-SGDのパラメータです。
DP-SGDのパラメータが$${C=\frac{b\sqrt{2}}{\sigma \sqrt{\eta n}}}$$を満たす際に、SGLDと等価になります。
今回はこの点に着目してSGLDを実装します。
実装
1. ライブラリのインポート
必要なライブラリをインポートします。
import sys
import os
import copy
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
!pip install 'opacus>=1.0'
import opacus
import warnings
warnings.simplefilter("ignore")2. 実行環境の確認
使用するライブラリのバージョンや、GPU環境を確認します。
Google Colaboratoryで実行した際の例になります。
print('Python:', sys.version)
print('PyTorch:', torch.__version__)
print('Opacus:', opacus.__version__)
!nvidia-smiPython: 3.10.12 (main, Jun 11 2023, 05:26:28) [GCC 11.4.0]
PyTorch: 2.0.1+cu118
Opacus: 1.4.0
Sat Sep 23 01:22:12 2023
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 525.105.17 Driver Version: 525.105.17 CUDA Version: 12.0 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 Tesla T4 Off | 00000000:00:04.0 Off | 0 |
| N/A 43C P8 9W / 70W | 0MiB / 15360MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=============================================================================|
| No running processes found |
+-----------------------------------------------------------------------------+3. データセットの作成
sinカーブに従うデータを作成します。
ただし、学習には[-1,1]の範囲のデータは使用しません。
def make_dataset(seed, plot=0, batch_size=64):
np.random.seed(seed)
x_true = np.linspace(-4, 4, 100)
y_true = np.sin(x_true)
x = np.concatenate([np.random.uniform(-4, -1, 500), np.random.uniform(1, 4, 500)])
y = np.sin(x)
# データをPyTorchのテンソルに変換
x = torch.from_numpy(x).float().view(-1, 1)
y = torch.from_numpy(y).float().view(-1, 1)
x_true = torch.from_numpy(x_true).float().view(-1, 1)
# グラフを描画
if plot == 1:
plt.plot(x_true, y_true)
plt.scatter(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
dataset = torch.utils.data.TensorDataset(x, y)
data_loader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True)
return data_loader
_ = make_dataset(0, plot=1)
4. ニューラルネットワークの定義
今回は3層の全結合ニューラルネットワークを用います。
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(1, 100)
self.fc2 = nn.Linear(100, 100)
self.fc3 = nn.Linear(100, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
5. 学習
SGLDの実装としては、opacusのDP-SGDの実装を利用します。
lr = 1e-2
batch_size = 16
sigma = 1.0
n_data = 1000
c = batch_size/sigma*np.sqrt(2/lr/n_data)
print('sigma:', sigma, 'c:', c)
device = "cuda" if torch.cuda.is_available() else "mps" if torch.backends.mps.is_available() else "cpu"
data_loader = make_dataset(0, batch_size=batch_size)
model = Net()
model = model.to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=lr, weight_decay=1e-4)
privacy_engine = opacus.PrivacyEngine()
model, optimizer, data_loader = privacy_engine.make_private(
module=model,
optimizer=optimizer,
data_loader=data_loader,
noise_multiplier=sigma,
max_grad_norm=c,
)
# 学習
model.train()
num_epochs = 100
loss_list = []
model_list = []
for epoch in range(num_epochs):
tmp_loss = []
for inputs, targets in data_loader:
inputs = inputs.to(device)
targets = targets.to(device)
# 順伝播と損失の計算
y_pred = model(inputs)
loss = criterion(y_pred, targets)
loss = loss.mean()
tmp_loss.append(loss.item())
# 勾配の初期化と逆伝播
optimizer.zero_grad()
loss.backward()
# パラメータの更新
optimizer.step()
tmp = copy.deepcopy(model)
model_list.append(tmp)
epsilon = privacy_engine.get_epsilon(1e-5)
print('epsilon', epsilon)
6. 予測
予測の事後分布の平均、標準偏差を描画します。
x_true = np.linspace(-4, 4, 100)
y_true = np.sin(x_true)
x_true = torch.from_numpy(x_true).float().view(-1, 1)
plt.figure(figsize=(9,4))
y_preds = []
for model in model_list:
model.eval()
x_true = x_true.to(device)
with torch.no_grad():
y_pred = model(x_true)
y_preds.append(y_pred.to('cpu').detach().numpy())
y_mean = np.mean(y_preds, axis=0)
y_std = np.sqrt(np.var(y_preds, axis=0) + 1e-4)
x_true = x_true.to('cpu')
plt.subplot(121)
plt.plot(x_true, y_true, label='True Function')
plt.plot(x_true, y_mean, label='Mean Prediction')
plt.fill_between(x_true.flatten(), y_mean.flatten() - y_std.flatten(), y_mean.flatten() + y_std.flatten(), alpha=0.3, label='Uncertainty')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.subplot(122)
plt.plot(x_true, y_std)
plt.xlabel('x')
plt.ylabel('Std')
plt.tight_layout()
plt.show()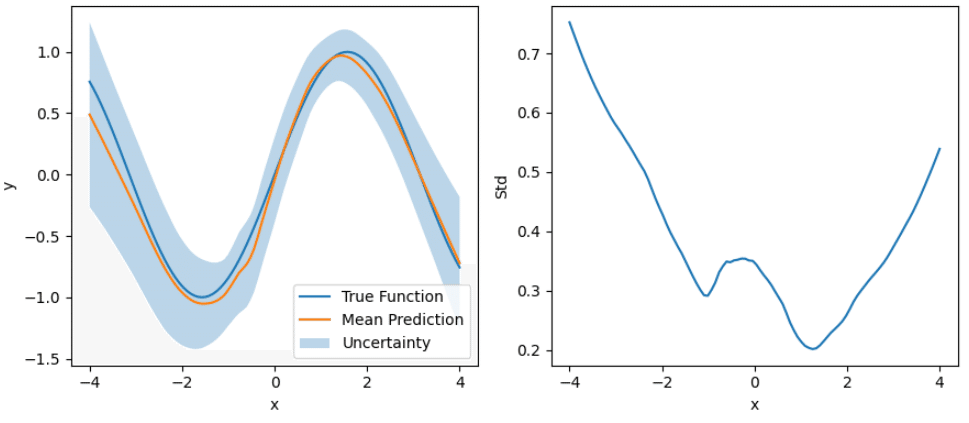
おわりに
今回の結果
予測の不確実性は、x最小値および最大値付近とデータが含まれない[-1,1]の範囲で大きくなっています。
データ数が少なく、予測が不確実と考えられる領域と、予測の標準偏差が大きい領域が一致しているため、想定通り予測の不確実性が算出できていると考えられます。
ただし、stochastic variational inferenceやMC dropoutと比較して、多くの教師データが必要となります。
次にやること
予測の不確実性を算出する他の手法も検証したいと思います。
参考資料
M. Welling and Y. W. Teh, Bayesian learning via stochastic gradient
Langevin dynamics, ICML, 2011.M. Abadi, et al., Deep learning with differential privacy, ACM CCS, 2016.
B. Li, et al., On connecting stochastic gradient MCMC and differential privacy, AISTATS, 2019.
