
浮力(ふりょく)のよく出る問題 (中学理科)
浮力とは何か、浮力が生まれる理由、アルキメデスの原理について、理解しておかないといけないポイントは次の4つです。
1、浮力=空気中での重さ-水中での重さ
2、浮力が生まれるわけ=上の面にはたらく水圧と下の面にはたらく水圧の差
3、水中にある体積100立方cmの物体にはたらく浮力は1N
4、浮力は水中にある物体の体積に比例するだけで、深さや物体の形は関係しない。
この稿では、上の4つのポイントをおさえた上で、いろいろな浮力の問題を解くときに必要になってくる大切なことがらをまとめます。
★浮力の意味がわかっているかどうかを問う問題
例題1:ある物体の重さをばねはかりではかったら1.2Nでした。そのまま、物体を水に入れると、物体全部が水に入り、ばねはかりの目盛りは0.8Nをさしました。

(1)物体にはたらいている浮力は何Nですか。
(2)物体の体積は何立方cmですか。
ただし、質量100gの物体にはたらく重力を1Nとします。
(解き方)
(1)「浮力=空気中での重さ-水中での重さ」より、空気中で測った物体の重さと、物体を水中に入れて測ったときの重さの差が、そのものにはたらいている浮力の大きさです。
だから、物体にはたらいている浮力は、
1.2N-0.8N=0.4N
です。
(2)「水中にある体積100立方cmの物体にはたらく浮力は1N」より、水中の物体にはたらいている浮力が0.4Nであれば、その物体の、水中に入っている部分の体積は40立方cmです。
この問題では物体全体が水に入っているので、この物体の体積は40立方cmです。
★ものが水に浮いているとき
例題2:質量60g、体積80立方cmの木片を水に入れたところ、木片は水に浮かびました。

(1)木片にはたらいている浮力の大きさは何Nですか。
(2)木片の、水中に沈んでいる部分の体積は何立方cmですか。
(3)木片の上に何N以上のおもりをのせると、木片は完全に水に沈みますか。
ただし、質量100gの物体にはたらく重力を1Nとします。
(解き方)
(1)物体が水に浮いているとき、なぜ物体が浮くかというと、下向きに物体を引っぱる重力(重さ)の大きさと、上向きに物体を支えている浮力の大きさが等しいから、物体は浮いているのです。
大切なこと:物体が浮いているときは、重さ=浮力
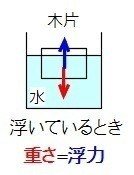
だから、質量60gの物体が浮いているとき、その物体にはたらいている重力は0.6Nであり、浮力も0.6Nです。
(2)「水中にある体積100立方cmの物体にはたらく浮力は1N」より、浮力が0.6Nだったので、木片の、水に沈んだ部分の体積は60立方cmです。
(3)体積が80立方cmの木片を完全に水中に沈めると、「水中にある体積100立方cmの物体にはたらく浮力は1N」より0.8Nの浮力が生まれます。
だから、この0.8Nの浮力にさからって木片を完全に水に沈めるには、0.8N以上の重さが必要です。
今、木片自体の重さが0.6Nだから、重さを0.8Nにするには、0.8-0.6=0.2N、あと0.2N以上の重さが必要です。
★浮力と全体の重さ
例題3:ビーカーに水を入れて台はかりで重さをはかったところ、台はかりの目盛りは3Nを示しました。
(1)水に重さが0.5Nで体積が10立方cmのおもりを沈めたら、台はかりの目盛りは何Nをさしますか。

(2)おもりをばねはかりにつるして、ゆっくりばねはかりを上にあげていくと、ばねはかりの目盛りが何Nのとき、おもりはビーカーの底を離れますか。
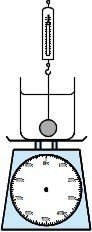
(3)おもりがビーカーの底を離れたとき、ビーカーの下の台はかりの目盛りは何Nをさしていますか。
(解き方)
(1)水に重さが0.5Nで体積が10立方cmのおもりを沈めたら、台はかりの目盛りは何Nをさしますか。

ビーカーと水を合わせた重さはが3Nで、おもりの重さが0.5Nです。
3Nと0.5Nを合わせた重さが下の台はかりにかかるので、台はかりの目盛りは3+0.5=3.5Nをさします。
このとき、おもりには「水中にある体積100立方cmの物体にはたらく浮力は1N」より、0.1Nの浮力がはたらいていますが、この浮力は、おもりを持ち上げようとすると浮力の分だけ軽くなるという意味しかありません(台はかりの、のせる台を上に持ち上げる力ではありません)。
だから、浮力がはたらいていても、浮力に関係なく、台はかりには水とビーカーとおもりの重さを合わせた重さがかかります。
(2)おもりをばねはかりにつりして、ゆっくりばねはかりを上にあげていくと、ばねはかりの目盛りが何Nのとき、おもりはビーカーの底を離れますか。

(3)おもりがビーカーの底を離れたとき、ビーカーの下の台はかりの目盛りは何Nをさしていますか。
(2)おもりの重さは0.5Nです。
そして、「水中にある体積100立方cmの物体にはたらく浮力は1N」より、体積10立方cmのおもりには0.1Nの浮力がはたらいています。
だから、ばねはかりでおもりを持ち上げるとき、0.5-0.1=0.4Nの力で持ち上げることができます。
(3)ばねはかりで持ち上げる前は、水とビーカー、そしておもりの重さを合わせた3.5Nの重さが下の台はかりにかかっていました。
ところが、その3.5Nの重さのうち、ばねはかりが上向きに0.4Nの力でおもりを引っ張ってくれることで、台はかりの台を押す力は0.4Nだけ減少します。
だから、下の台はかりの目盛りは3.5-0.4=3.1Nになります。
つまり、台はかりには、水とビーカーの重さの3Nに、浮力の0.1Nを加えた重さがかかっていることになります。
大切なこと:ビーカー・水・おもりの3つの重さが下の台はかりにかかる。
大切なこと:おもりをばねはかりで上に持ち上げるとき、ばねはかりの目盛りの分だけ、台はかりの目盛りは小さくなる。
台はかりにかかる力
=ビーカー+水+(おもりの重さ‐ばねはかりで上に引く力)
=ビーカー+水+浮力
★氷を水に浮かべたときの台はかりの目盛りと水面の高さ
例題4:重さ0.3N、体積33立方cmの氷をビーカーに入れた水の中に入れると、氷は一部を水面の上に出して水に浮かびました。このとき、台はかりの目盛りは1.5Nでした。

(1)水面より上に出ている氷の体積はいくらですか。
(2)氷がすべてとけたあとの台はかりの目盛りは何Nを示しますか。
(3)氷がすべてとけたあと、氷がとける前に比べて水面の高さはどうなっていますか。
(解き方)
(1)水面より上に出ている氷の体積はいくらですか。
氷が水に浮いているとき、氷の重さ=氷にはたらく浮力です。
氷の重さが0.3Nだから、氷にはたらいている浮力も0.3N、そして、「水中にある体積100立方cmの物体にはたらく浮力は1N」より、氷の水中に沈んでいる部分の体積は30立方cmです。
だから、水面より上に出ている氷の体積は33-30=3立方cmです。
(2)氷がすべてとけたあとの台はかりの目盛りは何gを示しますか。
ビーカー・水・氷の重さが下の台はかりにかかっています。
ビーカー+水+氷=1.5N
氷がとけてもこの関係に変化はありませんから、氷がすべてとけたあとの台はかりの目盛りは1.5Nのままです。
重さ0.3Nの氷が水に浮いているとき、氷にはたらいている浮力も0.3Nです。
この浮力は、氷にはたらく上向きの力であり、氷を水にうかべている力ですが、下の台はかりの台を上に持ち上げる力ではありません。
つまり、台はかりの目盛りには関係しません。
(3)氷がすべてとけたあと、氷がとける前に比べて水面の高さはどうなっていますか。
水は1gが1立方cmです。
だから、氷の重さが0.3Nのとき、「水中にある体積100立方cmの物体にはたらく浮力は1N」より、氷がとけて水になってしまうとその体積は30立方cmになります。
ところが、(1)で、氷の水中に沈んだ部分の体積は30立方cmでした。
つまり、氷のときも、とけて水になったあとも、氷によって増える体積は30立方cmのままで、かわりません。
水面の高さはずっと変化しません。
大切なこと:氷が水に浮かんでいるとき、氷がとけても水面の高さは変化しない。
★水以外の液体と浮力
「ものを水に入れると、ものがおしのけた体積の水の重さと同じだけ軽くなる」がアルキメデスの原理です。
水以外の液体にものを入れると、「ものがおしのけた体積の液体の重さと同じだけ軽くなる」ことになります。
例題5:体積40立方cmのおもりの重さをばねはかりではかったら1.2Nでした。おもりを密度0.8g/立方cmの液体に入れました。
(1)おもりにはたらいている浮力は何Nですか。
(2)おもりを液体に入れたあと、ばねはかりの目盛りは何Nを示しますか。
(解き方)
(1)水中におもりを入れたとき、おしのけた液体の体積は40立方cmであり密度は0.8g/立方cmなので、おしのけた液体の質量は0.8×40=32gです。
「ものがおしのけた体積の液体の重さと同じだけ軽くなる」ので、「水中にある体積100立方cmの物体にはたらく浮力は1N」より、おもりにはたらいている浮力は0.32Nです。
(2)「浮力=空気中での重さ-水中での重さ」より、水中では、空気中より浮力の分だけ軽くなります。
1.2-0.32=0.88Nだから、ばねはかりの目盛りは0.88Nを示します。
いいなと思ったら応援しよう!

